15 MathReview Tuesday 81500 1 Convexity and Concavity

15. Math-Review Tuesday 8/15/00 1

Convexity and Concavity z Consider the function f(x)=x 2 over the interval [-1, 1]. Is this function convex or concave? Prove it. 15. Math-Review 2

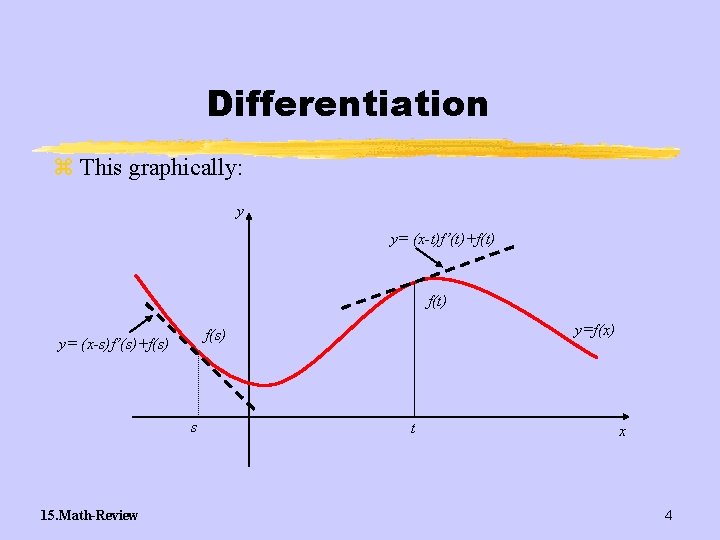
Differentiation z The derivative y The derivative of a function at a point is the instantaneous slope of the function at that point. This is, the slope of the tangent line to the function at that point. y Notation: for a function y = f(x), the derivative of f with respect to x can be written as: 15. Math-Review 3

Differentiation z This graphically: y y= (x-t)f’(t)+f(t) y= (x-s)f’(s)+f(s) s 15. Math-Review y=f(x) f(s) t x 4

Differentiation z Rules of differentiation: (a) f(x) = k (b) f(x) = ax (c) f(x) = xn => f’(x) = 0 => f’(x) = a => f’(x) = nxn– 1 y Example: f(x) = x 5 f(x) = x 2/3 f(x) = x– 2/5 15. Math-Review 5

Differentiation z Rules of differentiation: (d) f(x) = g(x) + h(x) (e) f(x) = kg(x) (f) f(x) = g(x)n => f’(x) = g’(x) + h’(x) => f’(x) = kg’(x) => f’(x) = n g’(x)g(x)n– 1 y Inverse rule as a special case of this: y Example: f(x) = 3 x 2 f(x) = 3 x 3 – 4 x 2 + 6 x – 20 f(x) = (3– 7 x)– 3 15. Math-Review 6

Differentiation z More rules of differentiation: (g) f(x) = g(x)h(x) => f’(x) = g’(x)h(x)+ g(x)h’(x) (h) (i) f(x) = g(h(x)) => f’(x) = g’(h(x))h’(x) y Inverse rule as a special case of this: y Example: product, quotient and chain for the following: g(x) = x+2, h(x) = 3 x 2 g(x) = 3 x 2 + 2, h(x) = 2 x – 5 g(x) = 6 x 2, h(x) = 2 x + 1 g(x) = 3 x, h(x) = 7 x 2 – 10 g(x) = 3 x + 6, h(x) = (2 x 2 + 5). (3 x – 2) 15. Math-Review 7

Differentiation z Even more rules of differentiation: (j) f(x) = ax => f’(x) = ln(a)ax (k) f(x) = ln(x) => f’(x) = 1/x y Example: f(x) = ex f(x) = ln(3 x 3 + 2 x+6) f(x) = ln(x-3) 15. Math-Review 8

Differentiation z Example: logs, rates and ratios: y For the following examples we will consider y a function of x, ( y(x) ). y Compute: y For this last example find an expression in terms of rates of changes of x and y. 15. Math-Review 9

Differentiation z A non-linear model of the demand for door knobs, relating the quantity Q to the sales price P was estimated by our sales team as Q = e 9. 1 P-0. 10 z Derive an expression for the rate of change in quantity to the rate of change in price. 15. Math-Review 10

Differentiation z To differentiate is a trade…. 15. Math-Review 11

Differentiation z Higher order derivatives: y The second derivative of f(x) is the derivative of f’(x). It is the rate of change of function f’(x). y Notation, for a function y=f(x), the second order derivative with respect to x can be written as: y Higher order derivatives are defined analogously. y Example: Second order derivative of 15. Math-Review f(x) = 3 x 2 -12 x +6 f(x) = x 3/4 -x 3/2 +5 x 12

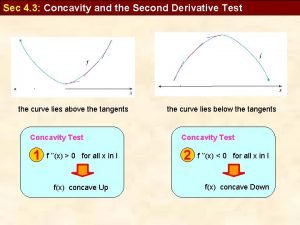
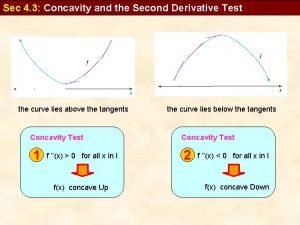
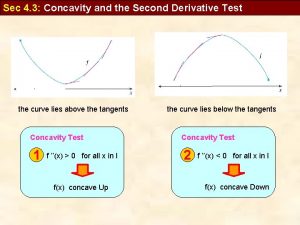
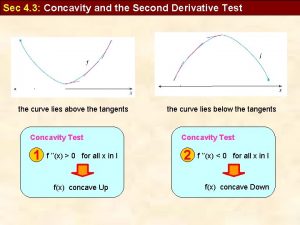
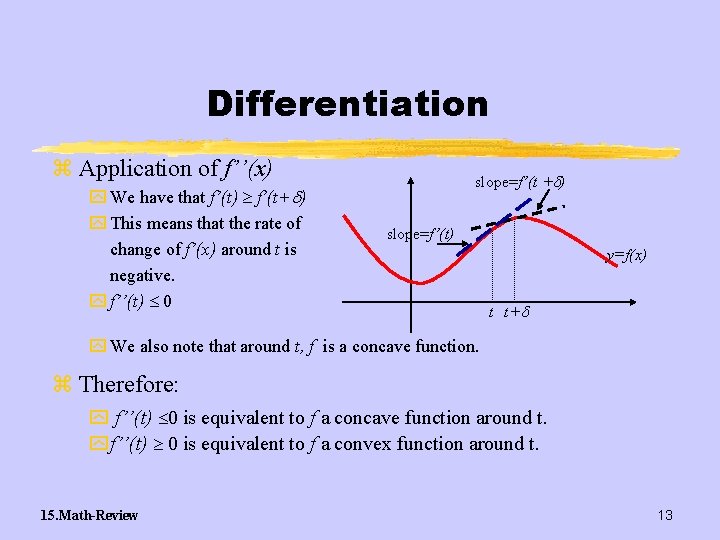
Differentiation z Application of f’’(x) y We have that f’(t) f’(t+ ) y This means that the rate of change of f’(x) around t is negative. y f’’(t) 0 slope=f’(t + ) slope=f’(t) y=f(x) t t+ y We also note that around t, f is a concave function. z Therefore: y f’’(t) 0 is equivalent to f a concave function around t. y f’’(t) 0 is equivalent to f a convex function around t. 15. Math-Review 13

Differentiation z Partial derivatives: y For functions of more than one variable, f(x, y), the rate of change with respect to one variable is given by the partial derivative. y The derivative with respect to x is noted: y The derivative with respect to y is noted: y Example: Compute partial derivatives w/r to x and y. f(x, y) = 2 x + 4 y 2 + 3 xy f(x, y) = (3 x – 7)(4 x 2 – 3 y 3) f(x, y) = exy 15. Math-Review 14

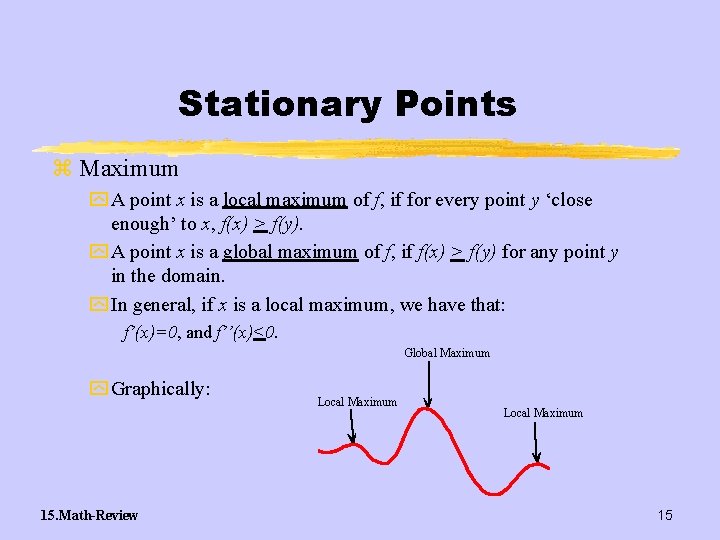
Stationary Points z Maximum y A point x is a local maximum of f, if for every point y ‘close enough’ to x, f(x) > f(y). y A point x is a global maximum of f, if f(x) > f(y) for any point y in the domain. y In general, if x is a local maximum, we have that: f’(x)=0, and f’’(x)<0. Global Maximum y Graphically: 15. Math-Review Local Maximum 15

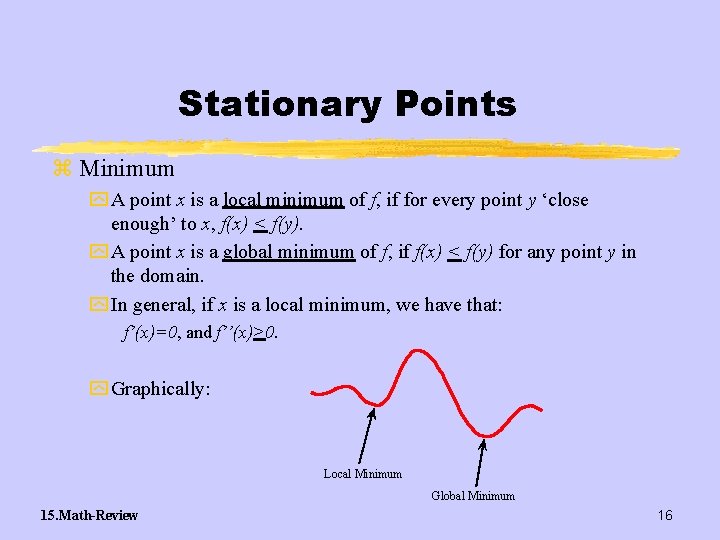
Stationary Points z Minimum y A point x is a local minimum of f, if for every point y ‘close enough’ to x, f(x) < f(y). y A point x is a global minimum of f, if f(x) < f(y) for any point y in the domain. y In general, if x is a local minimum, we have that: f’(x)=0, and f’’(x)>0. y Graphically: Local Minimum Global Minimum 15. Math-Review 16

Stationary Points z Example: y Consider the function defined over all x>0, f(x) = x - ln(x). y Find any local or global minimum or maximum points. What type are they? 15. Math-Review 17

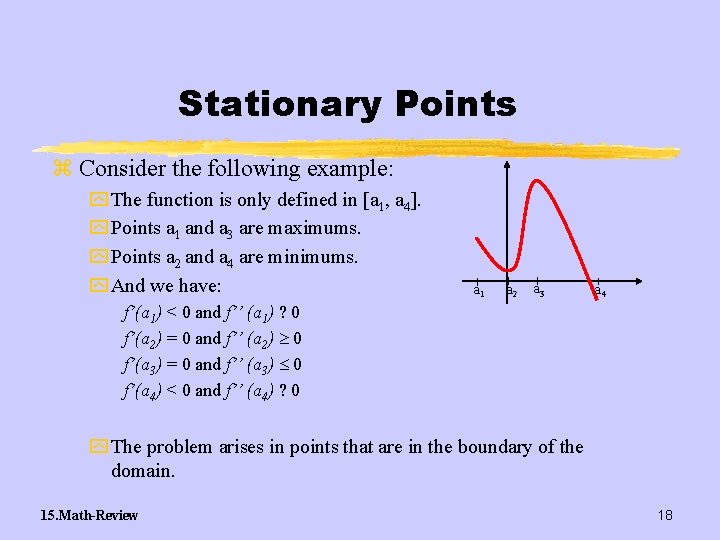
Stationary Points z Consider the following example: y The function is only defined in [a 1, a 4]. y Points a 1 and a 3 are maximums. y Points a 2 and a 4 are minimums. y And we have: a 1 a 2 a 3 a 4 f’(a 1) < 0 and f’’ (a 1) ? 0 f’(a 2) = 0 and f’’ (a 2) 0 f’(a 3) = 0 and f’’ (a 3) 0 f’(a 4) < 0 and f’’ (a 4) ? 0 y The problem arises in points that are in the boundary of the domain. 15. Math-Review 18

Stationary Points z Example: y Consider the function defined over all x [-3, 3], f(x) = x 3 -3 x+2. y Find any local or global minimum or maximum points. What type are they? 15. Math-Review 19

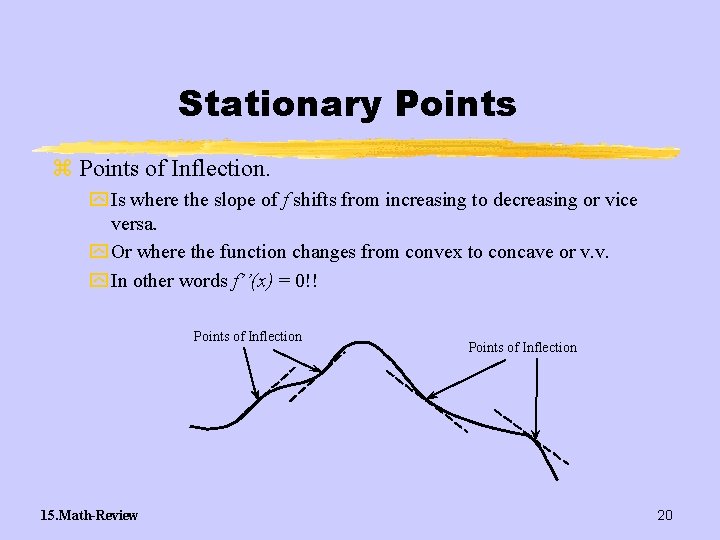
Stationary Points z Points of Inflection. y Is where the slope of f shifts from increasing to decreasing or vice versa. y Or where the function changes from convex to concave or v. v. y In other words f’’(x) = 0!! Points of Inflection 15. Math-Review Points of Inflection 20

Stationary Points z Finding Stationary Points y Given f(x), find f’(x) and f”(x). y Solve for x in f’(x) = 0. y Substitute the solution(s) into f”(x). x. If f”(x) 0, x is a local minimum. x. If f”(x) 0, x is a local maximum. x. If f”(x) = 0, x is likely a point of inflection. y Example: f(x) = x 2 – 8 x + 26 f(x) = x 3 + 4 x 2 + 4 x f(x) = 2/3 x 3 – 10 x 2 + 42 x – 3 15. Math-Review 21

Tough examples to kill time z Application of derivative: L’Hopital rule. z Use this rule to find a limit for f(x)=g(x)/h(x): 15. Math-Review 22

Tough examples to kill time z Example: y Let us consider the function Obtain a sketch of this function using all the information about stationary points you can obtain. y Sketch the function Hint: for this we will need to know that the ex ‘beats’ any polynomial for very large and very small x. 15. Math-Review 23