CONCAVITY AND THE SECOND DERIVATIVE TEST Section 3

CONCAVITY AND THE SECOND DERIVATIVE TEST Section 3. 4

When you are done with your homework, you should be able to… • Determine intervals on which a function is concave upward or concave downward • Find any points of inflection of the graph of a function • Apply the Second Derivative Test to find relative extrema of a function

I lived from 1642 -1715. I developed Calculus. I called Calculus “Fluents and Fluxions”. I discovered the law of gravity. I generalized the Binomial Theorem. Who am I? A. Fermat B. Newton C. Pythagoras D. Pascal

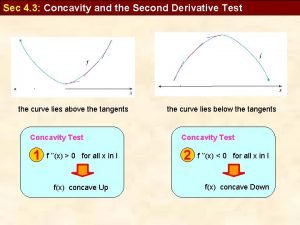
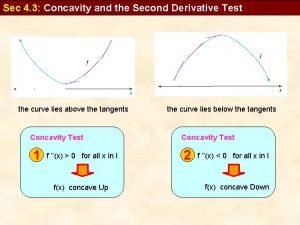
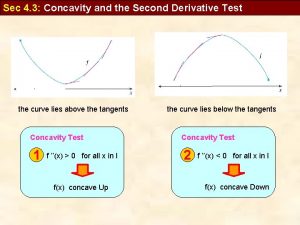
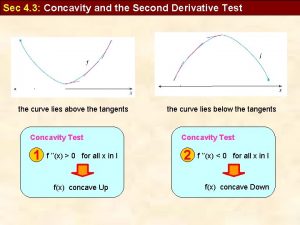
Definition of Concavity • Let f be differentiable on an open interval I. The graph of f is concave upward on I if is increasing on the interval and concave downward on I if is decreasing on the interval. concave down concave up

Theorem: Test for Concavity • Let f be a function second derivative exists on an open interval I. – If for all x in I, then f is concave upward in I. – If for all x in I, then f is concave downward in I.

Definition: Point of Inflection Let f be a function that is continuous on an open interval and let be a point in the interval. If the graph of I has a tangent line at this point , then this point is a point of inflection of the graph of f if the concavity of f changes from upward to downward (or downward to upward) at the point.

Theorem: Point of Inflection If is a point of inflection of the graph of f, then either or does not exist at Hmmm…. so this means that c is a __________ of the ______.

Guidelines for Determining Concavity on an Interval I and Finding Points of Inflection 1. Locate the critical numbers of Use these numbers to determine the test intervals. 2. Determine the sign of at one test value in each of the intervals. 3. Use theorem regarding the test for concavity to determine whether is concave upward or concave downward on each interval. 4. Examine the results of the test for a change in concavity to determine if there any inflection points.

Find the points of inflection and discuss the concavity of the graph of the function A. The function is concave upwards over its entire domain. There is a point of inflection at (0 , 3) B. The function is concave upwards on and concave downwards on C. The function is concave upwards over its entire domain and there are no points of inflection. D. None of the above

The most famous algebraist of the 1600’s was Fermat. Along with Pascal, he founded the subject of … A. B. C. D. Probability Number Theory Abstract Algebra All of the above.

5 cards are selected without replacement from a standard 52 card deck. Find the probability that all the cards are spades. This is called a straight flush in poker. A. B. C. D. E. Both B and D

Theorem: Second Derivative Test • Let f be a function such that and the second derivative of f exists on an open interval containing c. – If then f has a relative minimum at then f has a relative maximum at • If the test fails. That is, f may have a relative maximum, a relative minimum, or neither. In such cases, you can use the First Derivative Test.

The following function has a relative minimum at • 6856. 0 • 0. 0