Lesson 4 3 First and Second Derivative Test

Lesson 4 -3 First and Second Derivative Test for Relative Extrema

Quiz • Homework Problem: Differentials 3 -11 – f(x) = x 5 Use differentials to estimate f(2. 001) • Reading questions: – Where is the first derivative test performed to determine a relative extrema? – Where is the second derivative test performed to determine a relative extrema?

Objectives • Understand use the First Derivative Test to determine min’s and max’s • Understand use the Second Derivative Test to determine min’s and max’s

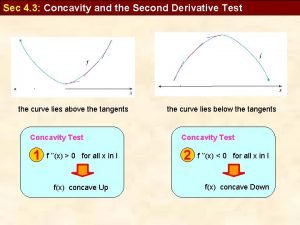
Vocabulary • Increasing – going up or to the right • Decreasing – going down or to the left • Inflection point – a point on the curve where the concavity changes

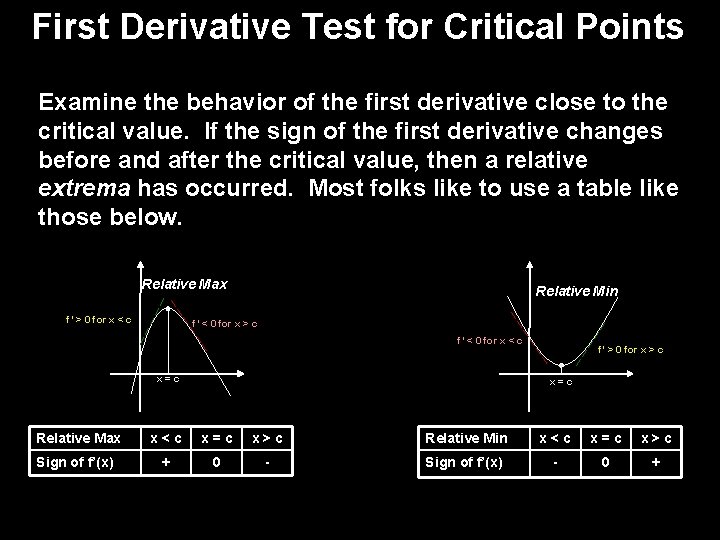
First Derivative Test for Critical Points Examine the behavior of the first derivative close to the critical value. If the sign of the first derivative changes before and after the critical value, then a relative extrema has occurred. Most folks like to use a table like those below. Relative Max f’ > 0 for x < c Relative Min f’ < 0 for x > c f’ < 0 for x < c x = c f’ > 0 for x > c x = c Relative Max x < c x = c x > c Relative Min x < c x = c x > c Sign of f’(x) + 0 - Sign of f’(x) - 0 +

Example 1 Determine analytically where f(x) = x / (1 + x²) is increasing or decreasing f’(x) = (1 + x²) (1) – (2 x) (x) / (1 + x²)² = (1 – x²) / (1 + x²)² f’(x) > 0 if |x| < 1 so -1 < x < 1 increasing f’(x) < 0 if |x| > 1 so x < -1 or x > 1 decreasing

Example 2 Use the first derivative test to determine relative extrema for f(x) = x 4 – 4 x 3 f’(x) = 4 x³ - 12 x² = 4 x² (x – 3) f’(x) = 0 if x = 0 or if x = 3 Interval x < 0 0 < x < 3 x > 3 f’(x) - + Since we have a slope going from – to + at x = 3, we have a relative minimum at x = 3. f(3) = -27

Example 3 Determine the concavity and inflection points of f(x) = x⅔(1 -x) f’(x) = (2 – 5 x) / (3 x⅓) f’’(x) = -2(5 x + 1) / (9 x 4/3) f’’(x) = 0 at x = -1/5 and f’’(x) = undefined at x = 0 Interval x < -1/5 < x < 0 x > 0 f’’(x) + - Therefore f(x) is concave up until x = -1/5 where it has an Inflection point and it is concave down afterwards

Second Derivative Test for Critical Points Examine the sign of the second derivative close at the critical value. If the sign of the second derivative is negative, then the function is concave down at that point and a relative maximum has occurred. If the sign of the second derivative is positive, then the function is concave up at that point and a relative minimum has occurred. Relative Max Relative Min x = c Relative Max x = c Relative Min x = c Sign of f’’(x) - Sign of f’’(x) + Note: rate of change of first derivative is always negative. Note: rate of change of first derivative is always positive.

Example 4 Use the second derivative test to identify relative extrema for g(x) = ½ x – sin x for (0, 2π). g’(x) = ½ - cos x g’(x) = 0 at π/3 and 5π/3 g’’(x) = sin x g’’(π/3 ) = √ 3/2 g’’(5π/3 ) = -√ 3/2 Therefore since g’’(π/3) > 0 a minimum occurs there and since g’’(5π/3) < 0 a maximum occurs there.

TI-89 Notation Notes When solve periodic functions (like sin and cos), our calculator often will give answers that are not easily interpreted. For example in the last problem when we solved cos x = ½ using our calculator we got: (6∙@n 1 + 1)∙π (6∙@n 1 -1)∙π x = ----------- or ----------- 3 3 With the TI-89 the calculator tries to give you the form of all answers. The “@n#” notation means to substitute an integer (1, 2, etc) in to get specific answers. For example: n x= x= 1 7π/3 2 13π/3 5π/3 The right-hand side answers are in our interval [0, 2π]

Example 5 Use the second derivative test to determine relative extrema for f(x) = x 4 – 4 x 3 f’(x) = 4 x³ - 12 x² = 4 x² (x – 3) f’(x) = 0 at x = 0 and x = 3 f’’(x) = 12 x² - 24 x = 12 x (x – 2) f’’(0) = 0 and f’’(3) = 36 Therefore a relative minimum occurs at x = 3

Example 6 Sketch the graph of f(x) over [0, 6] satisfying the following conditions: y f(0) = f(3) = 3 f(2) = 4 f(4) = 2 f(6) = 0 f’(x) > 0 on [0, 2) x f’(x) < 0 on (2, 4)(4, 5] f’(2) = f’(4) = 0 f’(x) = -1 on (5, 6) f’’(x) < 0 on (0, 3) (4, 5) f’’(x) > 0 on (3, 4)

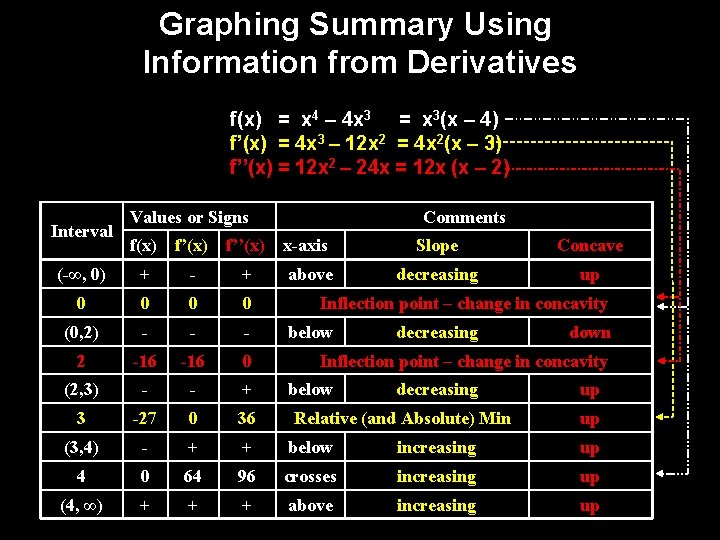
Graphing Summary Using Information from Derivatives f(x) = x 4 – 4 x 3 = x 3(x – 4) f’(x) = 4 x 3 – 12 x 2 = 4 x 2(x – 3) f’’(x) = 12 x 2 – 24 x = 12 x (x – 2) Interval Values or Signs f(x) f’(x) Comments f’’(x) x-axis Slope Concave above decreasing up (-∞, 0) + - + 0 0 (0, 2) - - - 2 -16 0 (2, 3) - - + 3 -27 0 36 (3, 4) - + + below increasing up 4 0 64 96 crosses increasing up (4, ∞) + + + above increasing up Inflection point – change in concavity below decreasing down Inflection point – change in concavity below decreasing Relative (and Absolute) Min up up

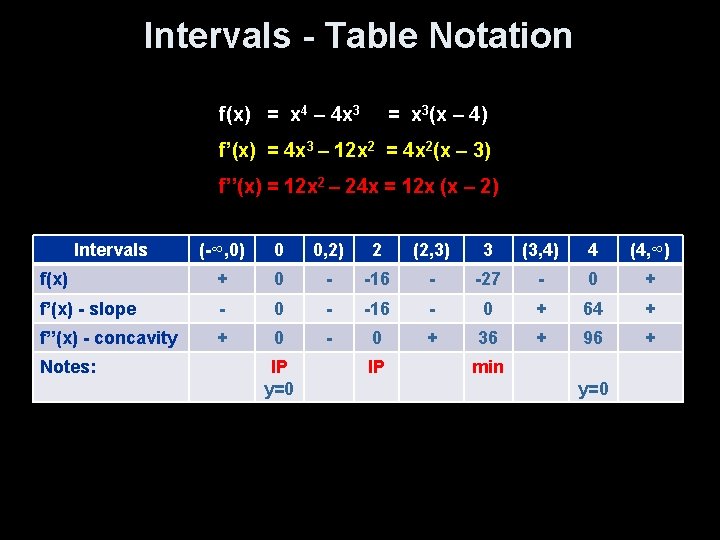
Intervals - Table Notation f(x) = x 4 – 4 x 3 = x 3(x – 4) f’(x) = 4 x 3 – 12 x 2 = 4 x 2(x – 3) f’’(x) = 12 x 2 – 24 x = 12 x (x – 2) Intervals (-∞, 0) 0 0, 2) 2 (2, 3) 3 (3, 4) 4 (4, ∞) f(x) + 0 - -16 - -27 - 0 + f’(x) - slope - 0 - -16 - 0 + 64 + f’’(x) - concavity + 0 - 0 + 36 + 96 + Notes: IP y=0 IP min y=0

Summary & Homework • Summary: – First derivative test looks at the slope before and after the critical value – Second derivative test looks at the concavity of the function at the critical value • Homework: – pg 304 -307: 1, 10, 11, 14, 17, 21, 27, 35, 38, 45, 74