1 PROGRESSO ARITMTICA E PROGRESSO GEOMTRICA MATEMTICA 2

1 PROGRESSÃO ARITMÉTICA E PROGRESSÃO GEOMÉTRICA MATEMÁTICA

2 O que estudaremos na aula de hoje? - PROGRESSÃO ARITMÉTICA - PA; - PROGRESSÃO GEOMÉTRICA - PG; - Resolução de Exercícios Propostos.

3

4 PROGRESSÃO ARITMÉTICA (PA)

5 PROGRESSÃO ARITMÉTICA (P. A. ) PA é toda sequência de números na qual: I - A partir do segundo termo, a diferença entre cada termo e o seu precedente (anterior) é CONSTANTE; ou II. Cada um de seus termos, exceto o primeiro, é igual ao precedente, precedente somado a um número CONSTANTE. somado Essa constante chama-se RAZÃO (r).

6 EXEMPLOS → ( 1, 5, 9, 13, 17, 21, . . . ) → ( 3, 12, 21, 30, 39, 48, . . . ) → ( 5, 5, . . . ) → ( 100, 90, 80, 70, 60, 50, . . . ) razão = 4 razão = 9 razão = 0 razão = -10 Podemos Classificar a PA das seguintes maneiras: • Se r > 0 => • Se r = 0 => • Se r < 0 => PA é crescente PA é constante PA é decrescente

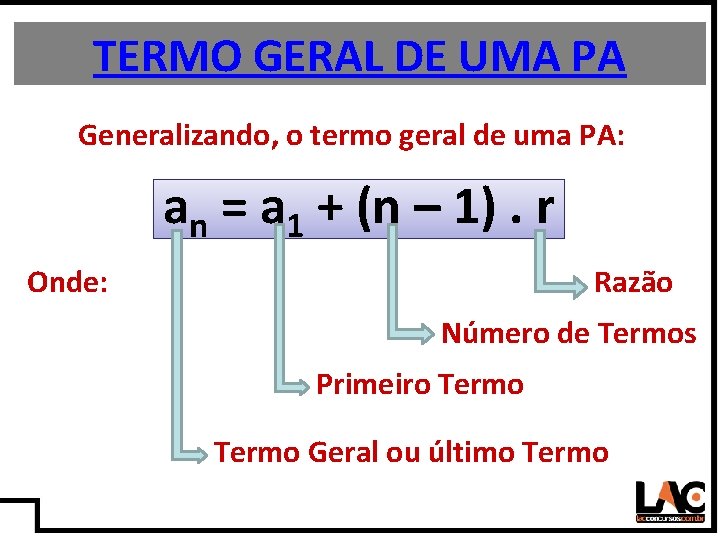
7 TERMO GERAL DE UMA PA Generalizando, o termo geral de uma PA: an = a 1 + (n – 1). r Onde: Razão Número de Termos Primeiro Termo Geral ou último Termo

8 EXEMPLO Um Policial, preparando-se para uma maratona, decide iniciar um treinamento da seguinte forma: no primeiro dia, corre 5 km. No segundo dia, aumenta a distância percorrida em 0, 2 km, correndo 5, 2 km; do terceiro dia em diante, ele sempre aumenta a distância percorrida em 0, 2 km, relativamente ao dia anterior. Após uma certa quantidade de dias, o corredor atinge, pela primeira vez, a marca dos 22 km, o que ocorre no A) 73º dia B) 85º dia C) 74º dia D) 86º dia E) 95º dia

9 EXEMPLO Um trecho de uma rodovia, do quilômetro 75 ao quilômetro 141, terá o asfalto renovado. Por isso, deverão ser fixadas placas de sinalização informando os motoristas sobre as obras. Será colocada uma placa no início e outra no final do trecho. As demais serão posicionadas de forma que a distância entre duas placas consecutivas seja sempre de 3 quilômetros. Nessas condições, o número total de placas de sinalização que deverão ser encomendadas pelo órgão competente é igual a A) 20 B) 21 C) 22 D) 23 E) 24

10 Propriedade Fundamental da PA Se os números x, y e z estão em PA, então: CONDIÇÃO DE EXISTÊNCIA DE UMA P. A. a 2 – a 1 = a 3 – a 2

11 EXEMPLO As medidas dos lados de um triângulo são expressas por x + 1, 2 x , x 2 - 5 e estão em P. A. , nesta ordem. O perímetro do triângulo vale: a) 8 b) 12 c) 15 d) 24 e) 33

12 SOMA DOS TERMOS DE UMA PROGRESSÃO ARITMÉTICA

13 SOMA DOS TERMOS DE UMA PA FINITA Sn = [(a 1 + an). n] 2 Onde: Sn → Soma dos n termos da PA a 1 → Primeiro termo da PA an → Último termo ou termo geral da PA n → número de termos

14 EXEMPLO Viviane iniciou a leitura de um livro com 538 páginas. No primeiro dia, ela leu 5 páginas, no segundo, ela leu duas páginas a mais que no primeiro dia. E assim por diante, a cada dia ela leu duas páginas a mais que no dia anterior. Assinale, após 19 dias de leitura, quantas páginas ainda faltam para ela ler. A) 101 B) 41 C) 207 D) 437 E) 311

15 PROGRESSÃO GEOMÉTRICA (PG)

16 SEQUÊNCIA – P. G. PG é toda sequência de números não-nulos na qual: I. a partir do segundo termo, o quociente da divisão de cada termo pelo seu precedente é CONSTANTE; ou II. Cada um de seus termos, exceto o primeiro, é igual ao precedente, precedente multiplicado por uma CONSTANTE. multiplicado Esse quociente ou fator é chamado de RAZÃO (q) da progressão geométrica.

17 EXEMPLOS → (5, 10, 20, 40, 80. . . ) razão = 2 → (8, 8, . . . ) razão = 1 → (27, 9, 3, 1/9, . . . ) razão = 1/3 → (2, -6, 18, -54, 162, . . . ) razão = -3 Podemos Classificar a PG das seguintes maneiras: Se r > 1 => Se r = 1 => Se 0 < r < 1 => Se r < 1 => PG é crescente PG é constante PG é decrescente PG é alternante

18 TERMO GERAL DE UMA PG an = a 1 n-1 . q Onde: an = termo geral; a 1 = 1 o termo da sequência; n = no de termos da PG (até an); q = razão.

19 EXEMPLO Considere a sequência numérica cujo termo geral é dado por an =21 -3 n, para n ≥ 1. Essa sequência numérica é uma progressão A) geométrica, cuja razão é 1/8. B) geométrica, cuja razão é -6. C) geométrica, cuja razão é -3. D) aritmética, cuja razão é -3. E) aritmética, cuja razão é 1/8.

20 EXEMPLO Uma cultura de bactérias contém inicialmente 10. 000 bactérias, as quais se reproduzem diariamente em progressão geométrica. Se ao final do quarto dia há 50. 625 bactérias na cultura, então o número de bactérias que havia ao final do segundo dia é de: A) 33750 B) 30312 C) 22500 D) 15000 E) 13500

21 CONDIÇÃO DE EXISTÊNCIA: Dada a sequência: (a 1, a 2, a 3, ……. , an )

22 EXEMPLO Três termos consecutivos de uma progressão geométrica crescente são x, x+20 e 2 x + 10. A razão dessa progressão é:

23