WYKAD 7 Spjno i rozpite drzewa Graf jest

WYKŁAD 7. Spójność i rozpięte drzewa • Graf jest spójny, gdy dla każdego podziału V na dwa rozłączne podzbiory A i B istnieje krawędź z A do B. • Definicja równoważna: Graf jest spójny, gdy każde dwa wierzchołki są połączone ścieżką (będącą podgrafem danego grafu). (ćw) • Ścieżka to graf postaci: V={v_1, . . . v_k}, E={v_1 v_2, . . . , v_{k-1}v_k}. Wierzchołki v_1 i v_k to końce ścieżki.

Składowe spójności • Relacja , , być połączonymi ścieżką” (tzn. być końcami ścieżki) jest relacją równoważności (zwrotna, symetryczna, przechodnia). (ćw) • Klasy abstrakcji tej relacji indukują składowe spójności grafu. • Inaczej, składowe spójności to maksymalne podgrafy spójne.

Wierzchołki i krawędzie cięcia • Wierzchołek v nazywamy wierzchołkiem cięcia grafu G, gdy podgraf G-v ma więcej składowych spójności niż G. • Krawędź e nazywamy krawędzią cięcia grafu G, gdy podgraf G-e ma więcej składowych spójności niż G. Wniosek: Krawędź e jest krawędzią cięcia grafu G, wgdy nie leży na żadnym cyklu w G. (ćw)

Minimalne grafy spójne • Ile najmniej krawędzi ma graf spójny G? • Jeśli G ma cykl, to można z niego usunąć dowolną krawędź bez rozspójniania G. • Wiemy, że jeśli e(G)>n-1, to G zawiera cykl (ćw). • Stąd, G ma co najwyżej n-1 krawędzi. • Wiemy też, że istnieje ciąg v_1, . . . , v_n taki, że dla każdego i istnieje j>i takie, że v_iv_j jest krawędzią (patrz: algorytm zachłanny). • Zatem e(G)=n-1.

Drzewa, lasy, liście • Drzewo to graf spójny bez cykli (a więc, minimalny graf spójny). • Las to graf acykliczny (a więc, rozłączna suma drzew) • Liść to wierzchołek wiszący drzewa. Fakt: Każde drzewo ma co najmniej dwa liście. Dowód: Spójrz na końce najdłuższej ścieżki. �

Własności drzew Tw. Dla spójnego grafu G, następujące warunki są równoważne: (i) T jest drzewem; (ii) e(T)=n-1; (iii) każde 2 wierzchołki są połączone dokładnie 1 ścieżką; (iv) każda krawędź jest krawędzią cięcia; (v) dla dowolnej krawędzi e nie należącej do G, graf G+e ma dokładnie 1 cykl.

Drzewa rozpięte • Drzewo rozpięte w grafie G, to podgraf T taki, że V(T)=V(G) i T jest drzewem. • Każdy graf spójny zawiera przynajmniej 1 rozpięte drzewo. • Graf pełny K_n ma ich n^{n-2} (Cayley, 1889)

Rozłączne rozpięte drzewa • Lepszą miarą spójności grafu jest maksymalna liczba rozłącznych rozpiętych drzew (RRD). • Jeśli G ma k RRD, to • Nie jest to jednak warunek dostateczny !

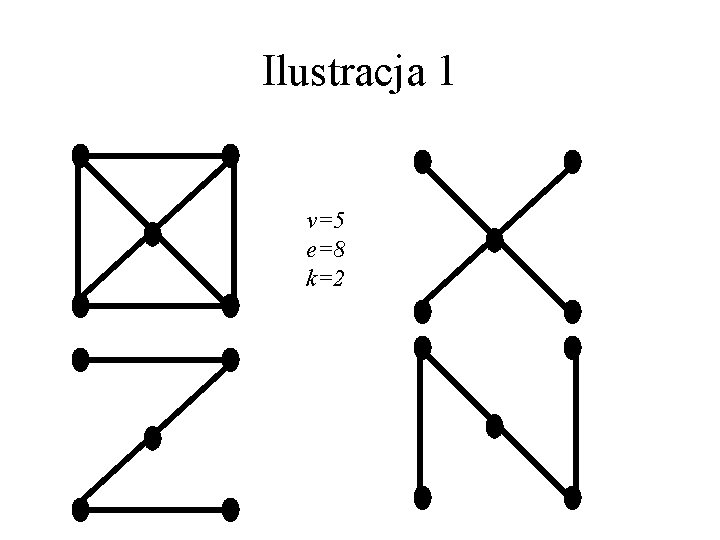
Ilustracja 1 v=5 e=8 k=2

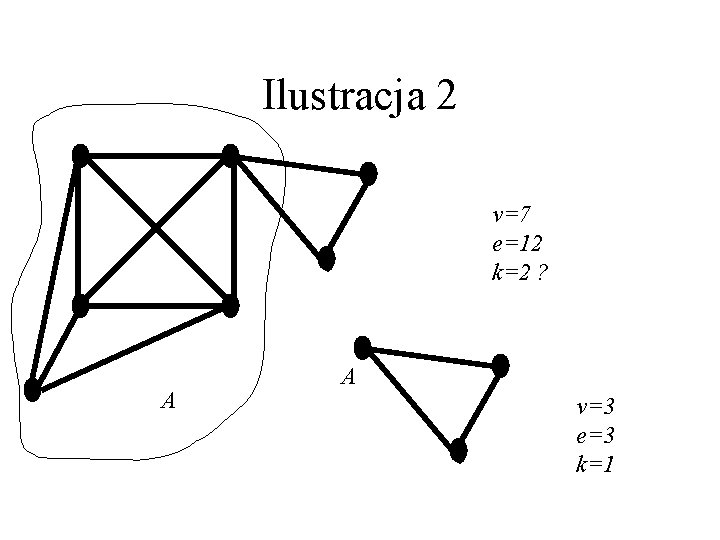
Ilustracja 2 v=7 e=12 k=2 ? A A v=3 e=3 k=1

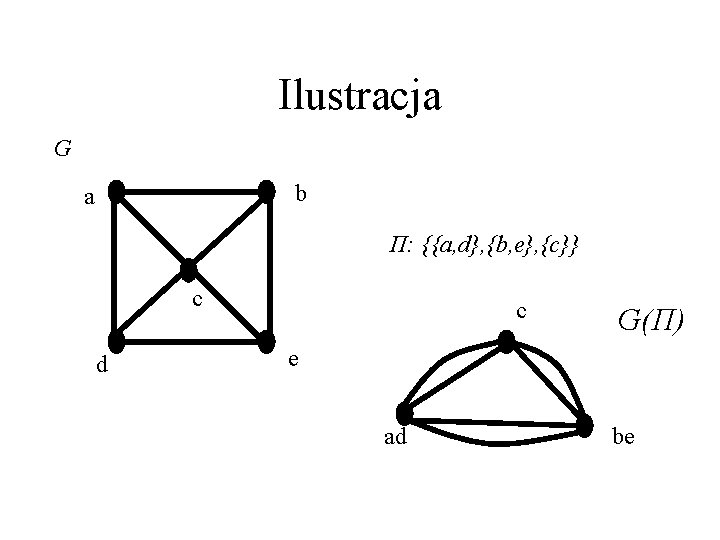
Dziel i ściągaj ! Dla danego podziału Π definiujemy multigraf G(Π)=(W, F), gdzie W={1, 2. . . , l}, a krotność krawędzi ij jest liczbą e(V_i, V_j) wszystkich krawędzi z V_i do V_j

Ilustracja G b a Π: {{a, d}, {b, e}, {c}} c d c G(Π) e ad be

Tw. Nash-Williamsa • Jeśli G jest spójny, to G(Π) też. (ćw) • Stąd, jeśli G ma k RRD T_1, . . . , T_k, to Tw. (Nash-Williams, 1961) G ma co najmniej k RRD wgdy powyższa nierówność zachodzi dla wszystkich podziałów Π zbioru V(G) na niepuste podzbiory. (Bez dowodu)

Odległości w grafie • Odległość d_G(u, v) między wierzchołkami u i v w spójnym grafie G to długość najkrótszej ścieżki łączącej u i v. • Odległość wierzchołków jest metryką (ćw) • Średnicą diam(G) grafu G nazywamy największą odległość w G. • Np. diam(K_n)=1, diam(C_{2 n})=n, diam(P_n)=n • Ale diam(K_n-e)=diam(K_{1, n})=2

Zastosowanie średnicy grafu • W pewnym kraju n miast ma lotniska. • Każde lotnisko może mieć nie więcej niż k bezpośrednich połączeń z innymi, a przynajmniej jedno ma ich mieć dokładnie k. • Chcemy optymalnie zaprojektować siatkę połączeń, by żadna podróż nie wymagała więcej niż d-1 przesiadek. • Jest to więc pytanie o

Przypadek d=2, k>n-6 e_2(n, n-1)=n-1 (weź G=K_{1, n-1}) Tw. Dla n>12 e_2(n, n-2)=e_2(n, n-5)=2 n-4 e_2(n, n-3)=e_2(n, n-4)=2 n-5 Dowód (k=n-2): Graf K_{2, n-2} daje oszacowanie z góry. Oszacowanie z dołu na ćwiczeniach.