UNIT 2 MEASUREMENTS UNITS DIMENSIONAL ANALYSIS conversions Number

UNIT 2 -MEASUREMENTS UNITS & DIMENSIONAL ANALYSIS (conversions)

Number vs. Quantity Ø A number without a unit is a “naked” number Ø Quantity - number + unit UNITS MATTER!!

Common SI Units Quantity Symb Base Unit Abbre ol v. l Length meter m v Volume Liter L m Mass kilogram kg Time t second s Temp T kelvin K Amount n mole mol

SI Units Ø Base units: w*Mass : w. Volume: w. Length: grams g Liters L meters m

SI Prefixs move right move left Prefix mega- Symbol M Factor 106 kilo- k 103 BASE UNIT --- 100 deci- d 10 -1 centi- c 10 -2 milli- m 10 -3 micro- 10 -6 nano- n 10 -9 pico- p 10 -12

SI Prefixes ØK ØH ØD ØU Ød Øc Øm Kilo Hecta Deka Unit (base) deci centi milli Kangaroos Have Dark Umbrellas during cloudy mornings

SI Conversions (short-cut) K H D U d c m 1. Count the number of places you have to move left or right. 2. Move the decimal that many places left or right. To the left or right?

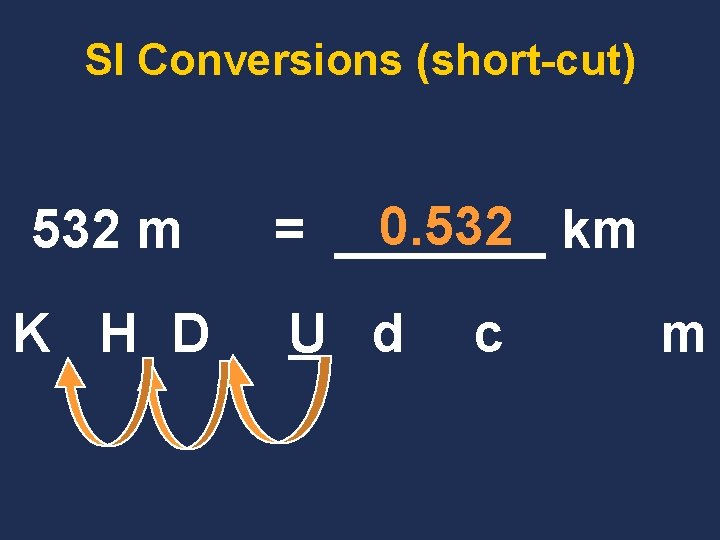
SI Conversions (short-cut) 532 m K H D 0. 532 km = _______ U d c m

SI Conversions (short-cut) 1) 20 cm = _______ m 0. 2 2) 0. 032 L = 32 _______ m. L 45, 000 3) 45 kg = _______ g 4) 805 dm = 80. 5 _______ m

Not all conversions can use the short-cut…. Hang on tight!! We’re going for a ride!

Dimensional Analysis A fancy word that means conversions

Dimensional Analysis Ø The “Factor-Label” Method: w A method used to “factor” out (cancel) labels (units)

Dimensional Analysis How many hours are in 10 days? -what info do you need to know first? - 24 hours in 1 day 10 days 24 hrs 1 day = 240 hrs

Dimensional Analysis Ø Conversion Factor: any ratio that equals one, used in converting Ø Ex: 4 quarters = 1 1 dollar Ø Ex: 1 kg = 1000 g 1

Dimensional Analysis Ø Steps: 1. Identify starting & ending units. 2. Line up conversion factors so units cancel. 3. Multiply all top numbers & divide by each bottom number. 4. Check units & answer.

Dimensional Analysis Ø How many seconds are in 36 hrs? hrs s 36 hrs 60 min 1 hr 60 sec 1 min = 129, 600 sec

Dimensional Analysis Brandeis football needs 550 cm for a 1 st down. How many yards is this? cm yd 550 cm 1 in 1 ft 1 yd 2. 54 cm 12 in 3 ft = 6. 0 yd

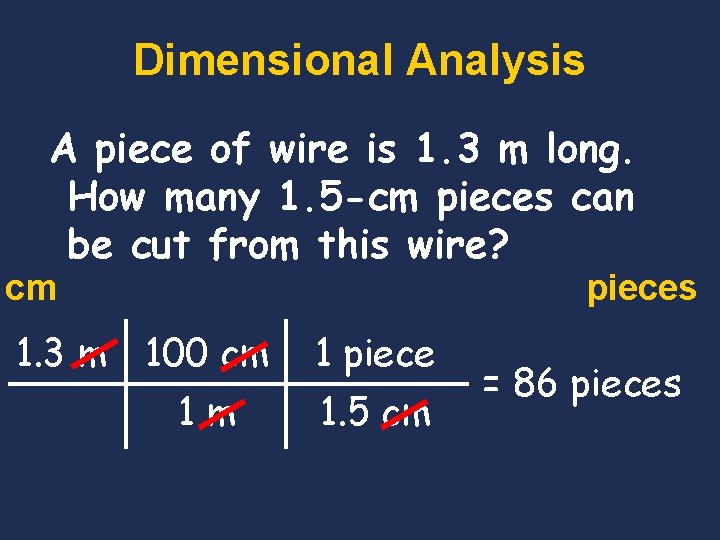
Dimensional Analysis A piece of wire is 1. 3 m long. How many 1. 5 -cm pieces can be cut from this wire? cm 1. 3 m pieces 100 cm 1 piece 1 m 1. 5 cm = 86 pieces

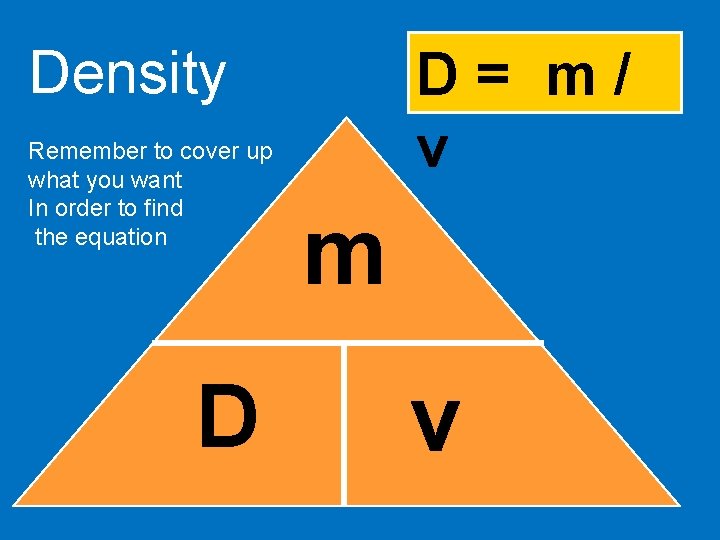
Density Remember to cover up what you want In order to find the equation D D= m/ v m v

Ø Formula: Density D = m/v w Units: ² Mass = g (grams) ² Volume = m. L or cm 3 ² Density = g/m. L or g/cm 3 REMEMBER TO COVER UP THE UNIT THAT YOU WANT IN ORDER TO FIND m D v

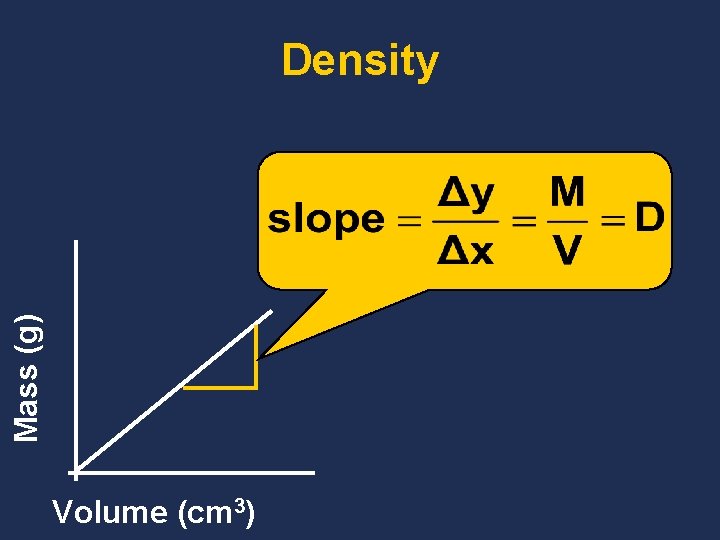
Mass (g) Density Volume (cm 3)

Derived Units Ø A Combination of base units. For example: 3 = 1 m. L 1 cm Ø Volume or w length 1 dm 3 = 1 L (m 3 cm 3) Ø Density (kg/m 3 or g/cm 3) w mass per volume M D= V

D. Density Ø An object has a volume of 825 cm 3 and a density of 13. 6 g/cm 3. Find its mass. GIVEN: WORK: V = 825 cm 3 D = 13. 6 g/cm 3 M=? M = DV m D v M = (13. 6 g/cm 3)(825 cm 3) M = 11, 200 g

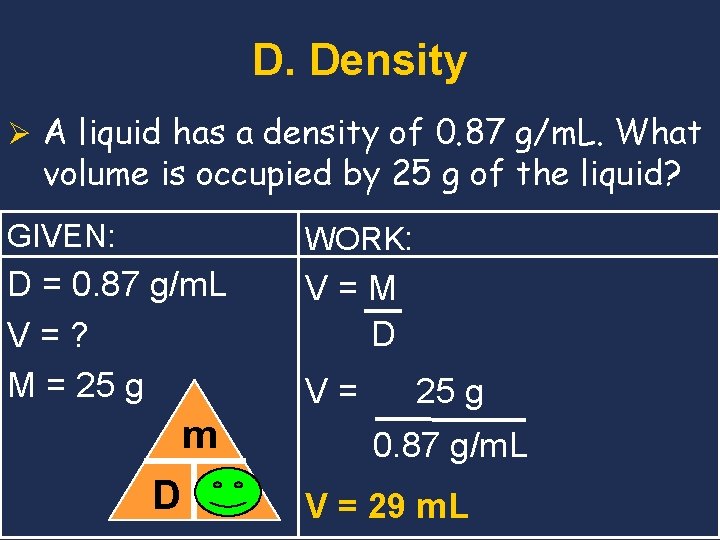
D. Density Ø A liquid has a density of 0. 87 g/m. L. What volume is occupied by 25 g of the liquid? GIVEN: WORK: D = 0. 87 g/m. L V=? M = 25 g V=M D m D v V= 25 g 0. 87 g/m. L V = 29 m. L