TWIERDZENIE TALESA Zastosowanie w matematyce i yciu codziennym

TWIERDZENIE TALESA Zastosowanie w matematyce i życiu codziennym

Tales z Miletu Był on gr. filozofem i matematykiem. Uważany był za jednego z siedmiu mędrców czasów starożytnych i za ojca nauki greckiej. Być może ze względu na jego wielostronne zainteresowania. Jeden z twórców jońskiej teorii filozofii przyrody. Zapoczątkował poszukiwanie pierwszej zasady w filozofii. Interesował się astronomią i matematyką, dowodem na to jest np. : przewidzenie przez Talesa zaćmienia słońca, które miało miejsce w dn. 18 maja 585 roku. Tales założył jońską szkołę filozofii przyrody, był aktywny politycznie i gospodarczo szczególnie w stosunku do Babilonu, Egiptu i Fenicji. Zasady geometrii przyswoił sobie będąc w Egipcie, tam obliczył wysokość piramid za pomocą ich cienia.

Przypisuje mu się następujące odkrycia: • o przepołowieniu koła przez średnicę, • dwa kąty przy podstawie trójkąta równoramiennego są równe, • jeżeli dwie linie proste przecinają się, przeciwległe kąty są równe, • kąt wpisany w półkole jest kątem prostym • trójkąt jest określony, jeżeli dana jest jego podstawa i kąty przy podstawie.

Tales jako filozof W zakresie filozofii Tales stworzył ogólną zasadę z której powstała wszelka natura, nosiła ona miano „arche”. Wg niego była to woda. Woda jest przyczyną wszelkiego życia. Ziemia pływa na wodach oceanu. Woda w jego kosmologii odgrywała rolę wiecznej substancji nadającej żywotność wszelkiej materii. Nie uznawał on bogów mitologicznych. W jego racjonalistycznych koncepcjach nie było na to miejsca. Interpretacja świata była świecka: sztormów morskich nie powodował Posejdon, ale wiatry. Platon wspomina anegdotę dotyczącą Talesa, który jakoby poszedł wraz ze służącą obserwować w ciemności gwiazdy. Nie spostrzegł on dołu, wpadł do niego i potłukł się. Pomocnica zaś miała mu dogryźć, iż chciał zobaczyć, co się dzieje na niebie, a nie dostrzegł, co znajduje się pod jego nogami.

proporcje Proporcja – równość dwóch stosunków postaci lub W zapisie tym a i d nazywamy wyrazami skrajnymi, b i c – środkowymi.

Własności proporcji • Podstawowa własność proporcji mówi, że iloczyn wyrazów skrajnych jest równy iloczynowi wyrazów środkowych.

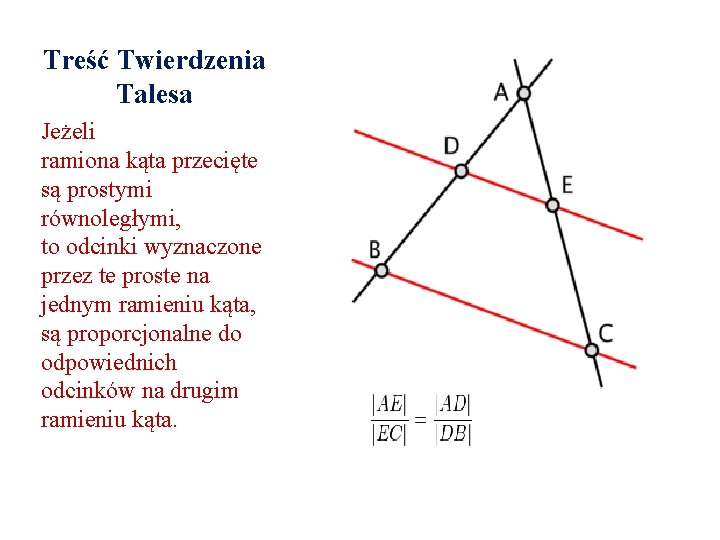
Treść Twierdzenia Talesa Jeżeli ramiona kąta przecięte są prostymi równoległymi, to odcinki wyznaczone przez te proste na jednym ramieniu kąta, są proporcjonalne do odpowiednich odcinków na drugim ramieniu kąta.

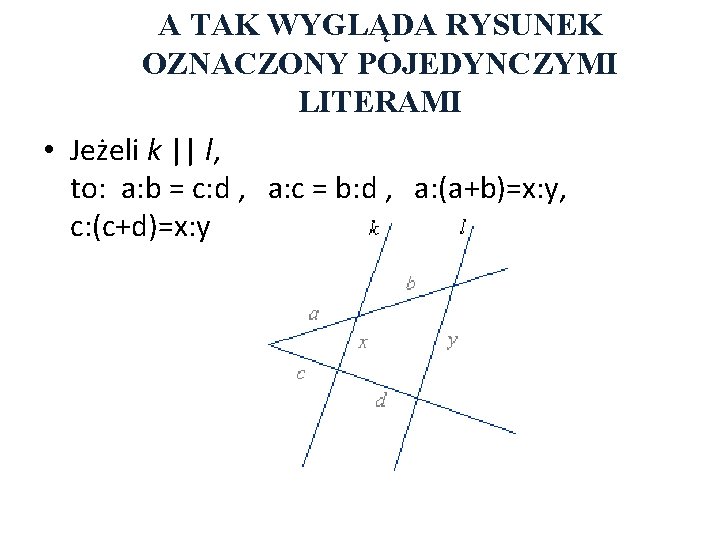
A TAK WYGLĄDA RYSUNEK OZNACZONY POJEDYNCZYMI LITERAMI • Jeżeli k || l, to: a: b = c: d , a: c = b: d , a: (a+b)=x: y, c: (c+d)=x: y

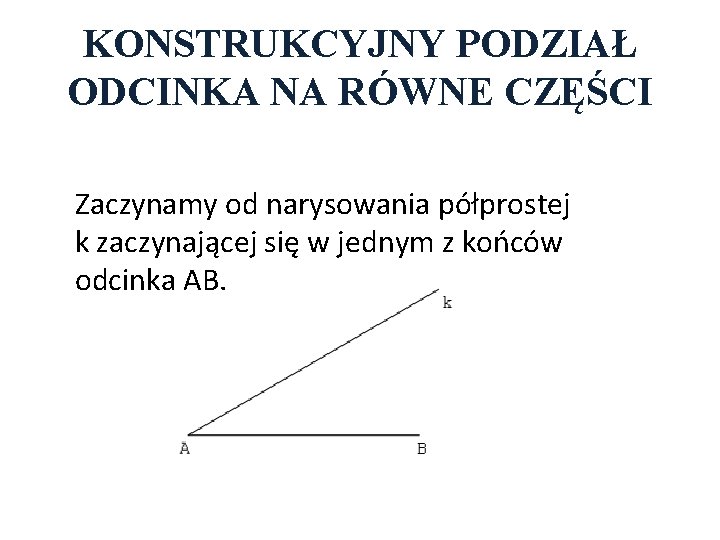
KONSTRUKCYJNY PODZIAŁ ODCINKA NA RÓWNE CZĘŚCI Zaczynamy od narysowania półprostej k zaczynającej się w jednym z końców odcinka AB.

KONSTRUKCYJNY PODZIAŁ ODCINKA NA RÓWNE CZĘŚCI Teraz cyrkiel rozstawiamy na dowolną rozwartość. Stawiamy nóżkę cyrkla na złączeniu odcinka AB i półprostej k (tutaj punkt A) i zaznaczamy odległość na półprostej k. Tak powstaje punkt M.

KONSTRUKCYJNY PODZIAŁ ODCINKA NA RÓWNE CZĘŚCI Dalej, nie zmieniając rozwartości cyrkla, stawiamy nóżkę w punkcie M i odmierzamy ponownie odległość na półprostej k. Powstaje punk N. Całość powtarzamy tyle razy, na ile części musimy podzielić odcinek. Nasz dzielimy na 3 części. Dwie już mamy odmierzone, więc zaznaczamy jeszcze jedną stawiając nóżkę cyrkla w punkcie N. Powstaje punkt L.

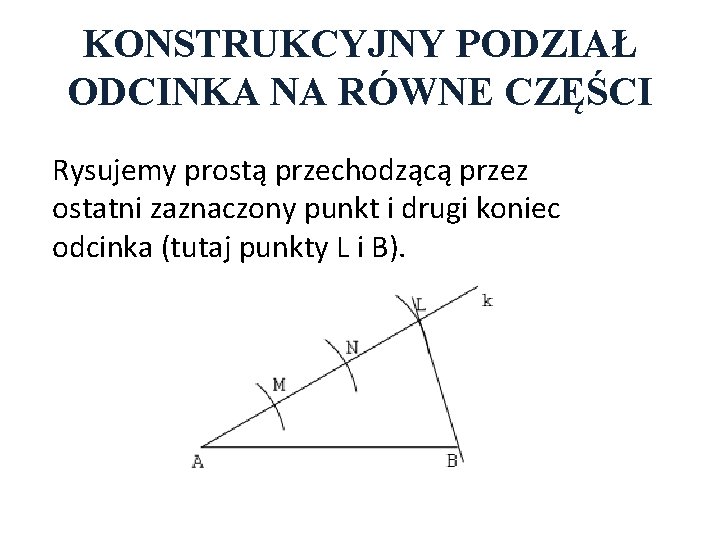
KONSTRUKCYJNY PODZIAŁ ODCINKA NA RÓWNE CZĘŚCI Rysujemy prostą przechodzącą przez ostatni zaznaczony punkt i drugi koniec odcinka (tutaj punkty L i B).

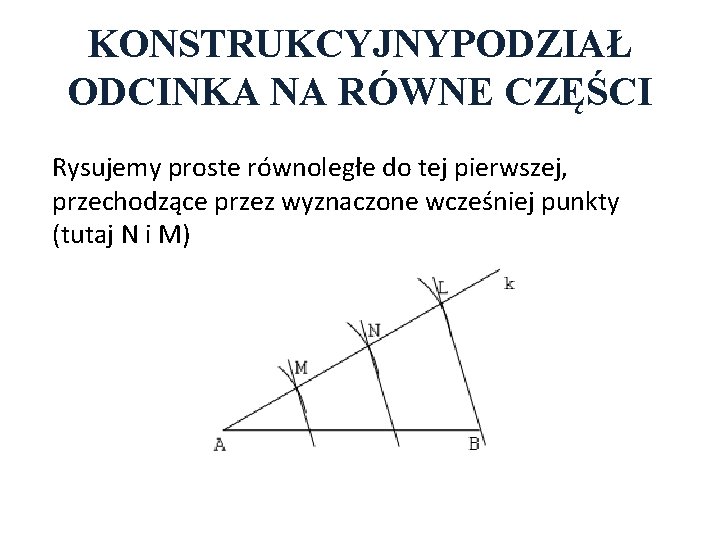
KONSTRUKCYJNYPODZIAŁ ODCINKA NA RÓWNE CZĘŚCI Rysujemy proste równoległe do tej pierwszej, przechodzące przez wyznaczone wcześniej punkty (tutaj N i M)

Twierdzenie odwrotne do twierdzenia Talesa Jeżeli ramiona kąta przecięte są kilkoma prostymi i stosunki długości odcinków na jednym ramieniu kąta równe są stosunkom długości odpowiednich odcinków na drugim ramieniu kąta, to te proste są równoległe.

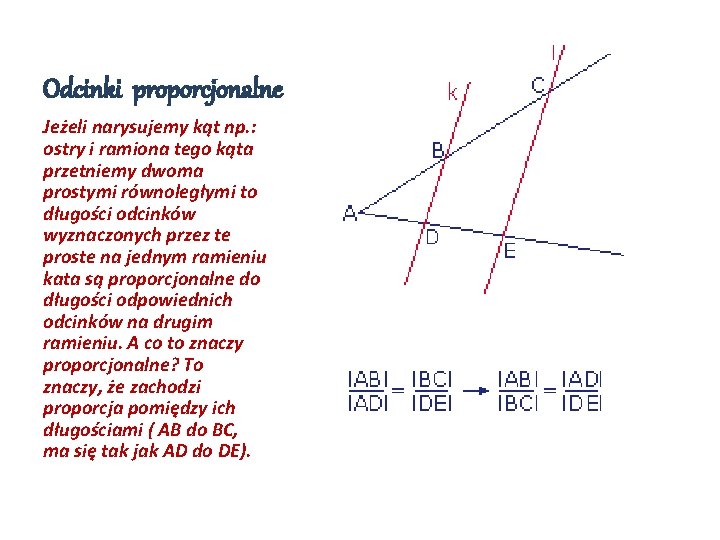
Odcinki proporcjonalne Jeżeli narysujemy kąt np. : ostry i ramiona tego kąta przetniemy dwoma prostymi równoległymi to długości odcinków wyznaczonych przez te proste na jednym ramieniu kata są proporcjonalne do długości odpowiednich odcinków na drugim ramieniu. A co to znaczy proporcjonalne? To znaczy, że zachodzi proporcja pomiędzy ich długościami ( AB do BC, ma się tak jak AD do DE).

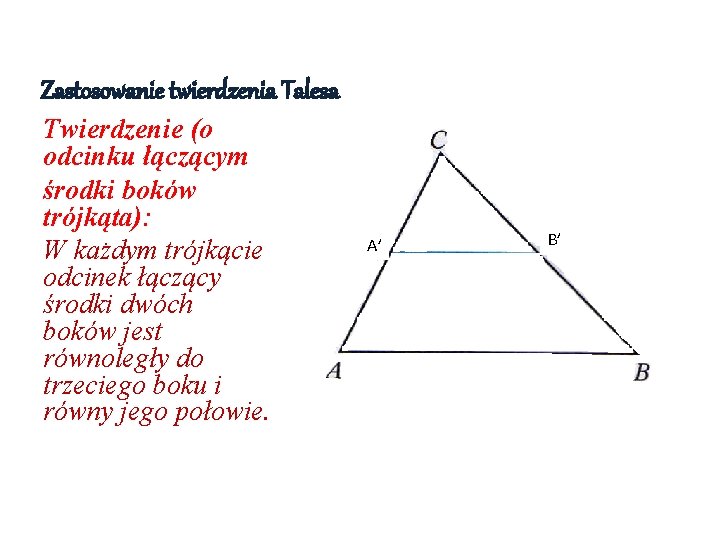
Zastosowanie twierdzenia Talesa Twierdzenie (o odcinku łączącym środki boków trójkąta): W każdym trójkącie odcinek łączący środki dwóch boków jest równoległy do trzeciego boku i równy jego połowie. A’ B’

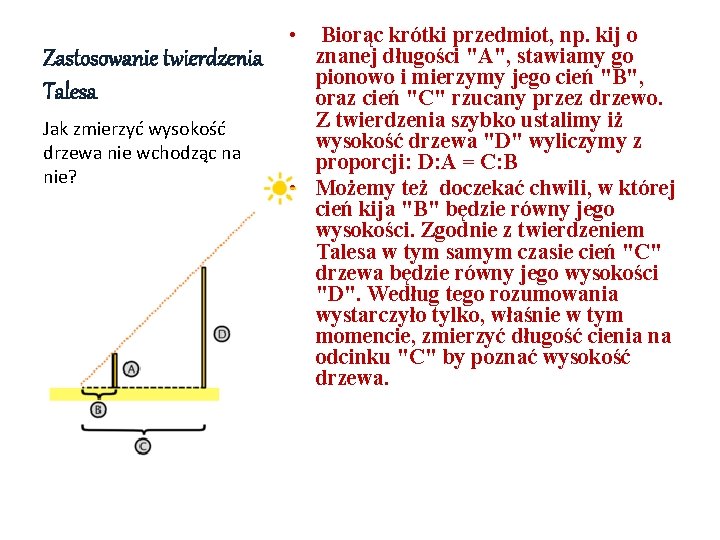
Zastosowanie twierdzenia Talesa Jak zmierzyć wysokość drzewa nie wchodząc na nie? • Biorąc krótki przedmiot, np. kij o znanej długości "A", stawiamy go pionowo i mierzymy jego cień "B", oraz cień "C" rzucany przez drzewo. Z twierdzenia szybko ustalimy iż wysokość drzewa "D" wyliczymy z proporcji: D: A = C: B • Możemy też doczekać chwili, w której cień kija "B" będzie równy jego wysokości. Zgodnie z twierdzeniem Talesa w tym samym czasie cień "C" drzewa będzie równy jego wysokości "D". Według tego rozumowania wystarczyło tylko, właśnie w tym momencie, zmierzyć długość cienia na odcinku "C" by poznać wysokość drzewa.

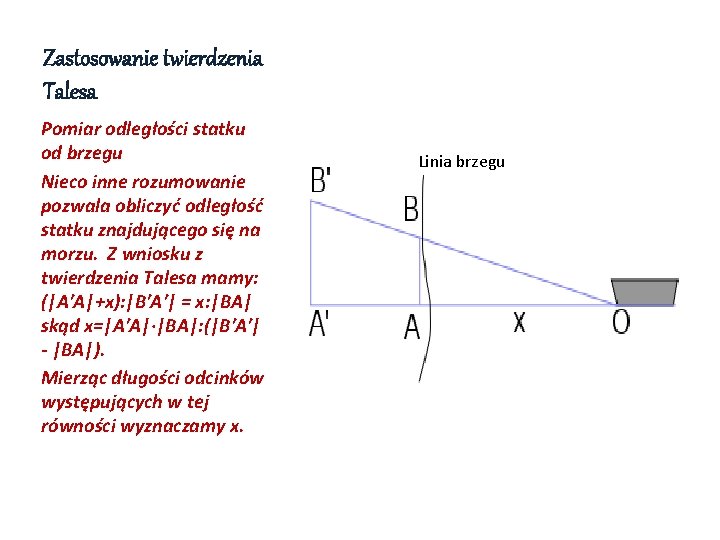
Zastosowanie twierdzenia Talesa Pomiar odległości statku od brzegu Nieco inne rozumowanie pozwala obliczyć odległość statku znajdującego się na morzu. Z wniosku z twierdzenia Talesa mamy: (|A′A|+x): |B′A′| = x: |BA| skąd x=|A′A|·|BA|: (|B′A′| - |BA|). Mierząc długości odcinków występujących w tej równości wyznaczamy x. Linia brzegu

Wykonała : Martyna Gawryś uczennica klasy III Publicznego Gimnazjum w Klwowie