Tree Automata First A reminder on Automata on
















- Slides: 22

Tree Automata First: A reminder on Automata on words Typing semistructured data

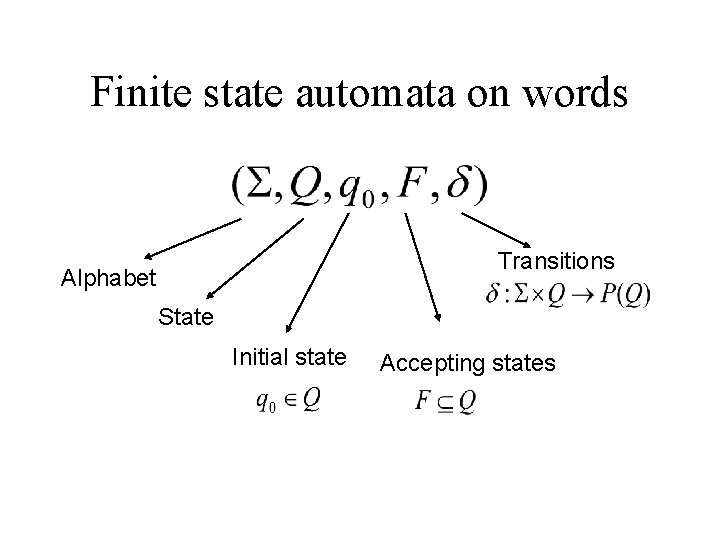
Finite state automata on words Transitions Alphabet State Initial state Accepting states Typing semistructured data

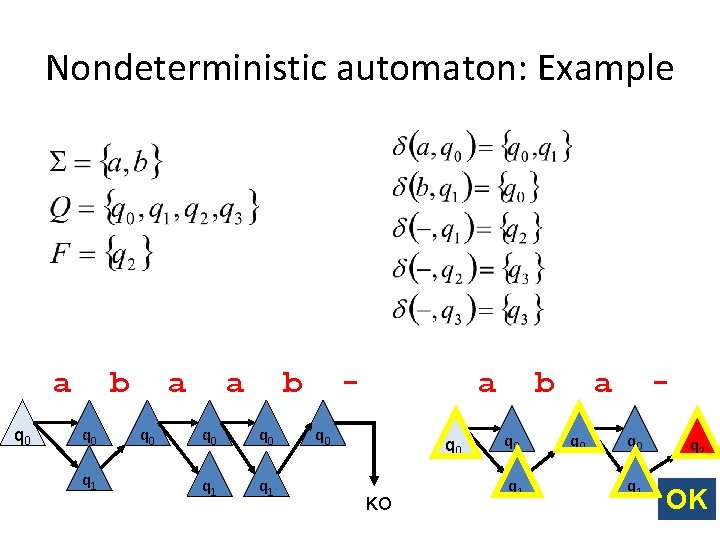
Nondeterministic automaton: Example a q 0 b q 0 q 1 a q 0 a b q 0 q 1 a q 0 KO b q 0 q 1 a q 0 q 1 q 2 OK

Reminder • Deterministic – No transition – No alternative transitions such as • Determinization – It is possible to obtain an equivalent deterministic automaton – State of new automaton = set of states of the original one – Possible exponential blow-up • Minimization • Limitations – cannot do – Context-free languages • Essential tool – e. g. , lexical analysis

(Reminder (2 • • L(A) = set of words accepted by automata A Regular languages Can be described by regular expressions, e. g. a(b+c)*d Closed under complement • Closed under union, intersection – Product automata with states (s, s’) where s is from A and s’ is from A’

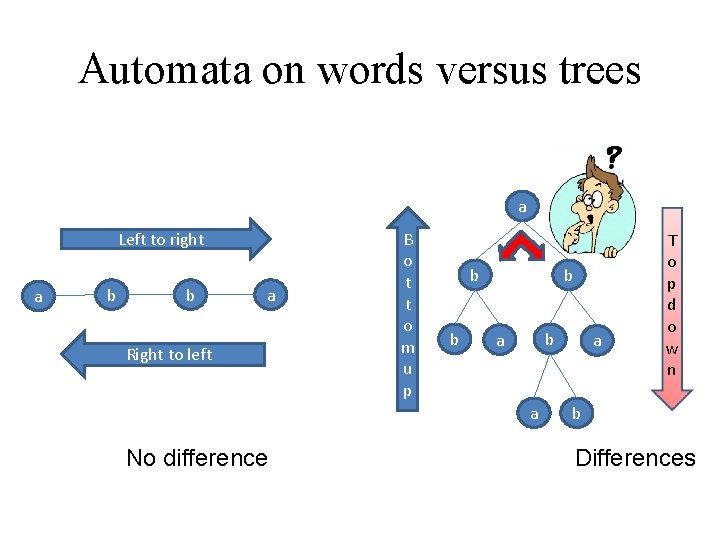
Automata on words versus trees a Left to right a b b a Right to left B o t t o m u p b b a a No difference a T o p d o w n b Differences

Automata on ranked trees Typing semistructured data

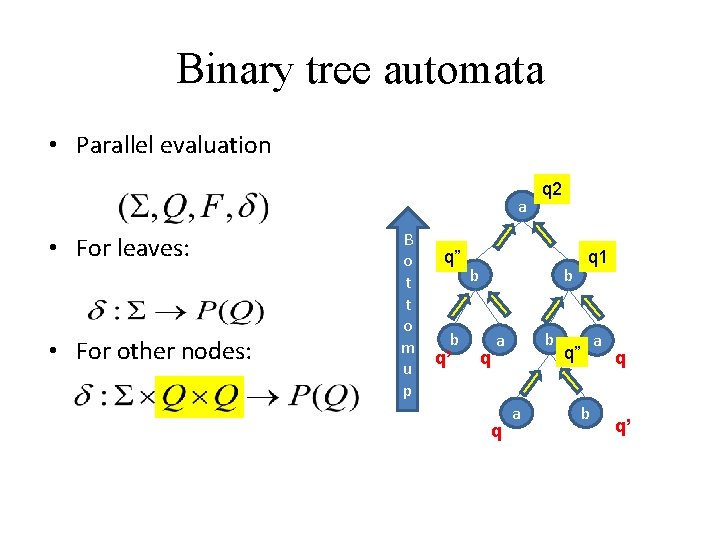
Binary tree automata • Parallel evaluation a • For leaves: • For other nodes: B o t t o m u p q” b q’ b b q b a q Typing semistructured data q 2 a q 1 a q” b q q’

Bottom-up tree automata • Bottom-up: if a node labeled a has its children in states q, q’ then the node moves nondeterministically to state r or r’ • Accepts is the root is in some state in F • Not deterministic if alternatives or -transitions:

Example: deterministic bottom-up

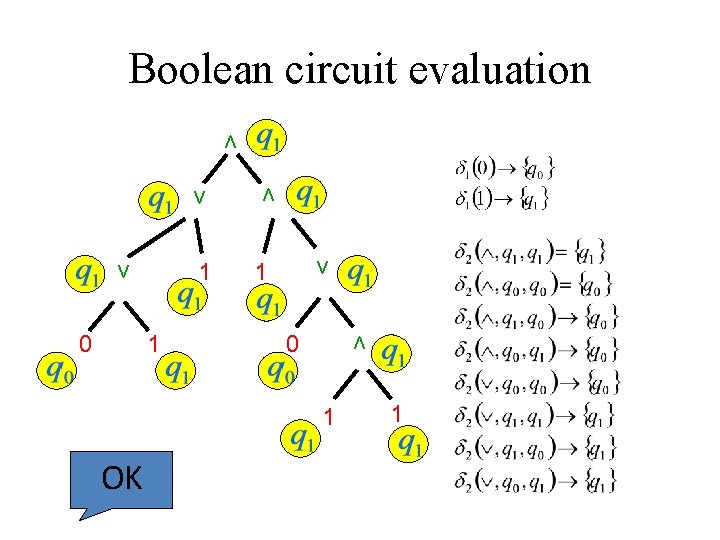
Boolean circuit evaluation v 1 1 v 0 v 1 0 v v v 1 OK 1

Regular tree language = set of trees accepted by a bottom-up tree automaton Typing semistructured data

Regular tree languages Theorem: the following are equivalent – L is a regular tree language – L is accepted by a nondeterministic bottom-up automaton – L is accepted by a nondeterministic top-down automaton Deterministic top-down is weaker

Top-down tree automata • Top-down: if a node labeled a is in state q”, then its left child moves to state q, right to q’ • Accepts is all leaves are in states in F • Not deterministic if

Why deterministic top-down is weaker? • Consider the language – L = { <r> <a>, <b> <r>, <r> <b>, <a><r>) } • It can be accepted by a bottom-up TA – Exercise: write a BUTA A such that L = L(A) • Suppose that B is a deterministic top-down TA that accepts both trees in L – Exercise: Show that B also accepts <r> <a> <r> – A contradiction Fact: No deterministic top-down tree automata accepts exactly L

Ranked trees automata: Properties • • Like for words Determinization Minimization Closed under – Complement – Intersection – Union

…But • XML documents are unranked: book (intro, section*, conclusion)

Automata on unranked tree Typing semistructured data

Unranked tree automata Issue: represent an infinite set of transitions Solution: a regular language

(Unranked tree automata (2 • Rule: • Meaning: if the states of the children of some node labeled a form a word in L(Q), this node moves to some state in {r 1, …, rm}

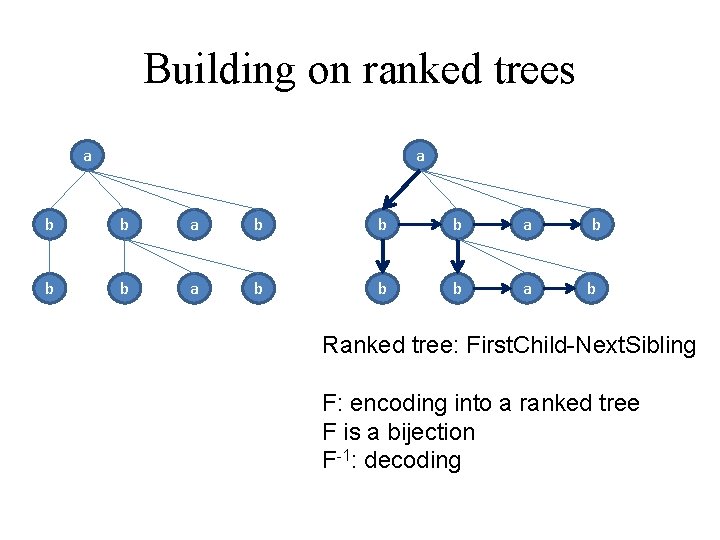
Building on ranked trees a a b b b a b b Ranked tree: First. Child-Next. Sibling F: encoding into a ranked tree F is a bijection F-1: decoding

Building on bottom-up ranked trees (2) • For each Unranked TA A, there is a Ranked TA accepting F(L(A)) • For each Ranked TA A, there is an unranked TA accepting F-1(L(A)) • Both are easy to construct Consequence: Unranked TA are closed under union, intersection, complement Determinaztaion also possible, a bit more tricky
 Thesis reminder
Thesis reminder Stir you up by way of reminder
Stir you up by way of reminder Phytel appointment reminder
Phytel appointment reminder What does it mean
What does it mean Civil surgeon worksheet
Civil surgeon worksheet How to uncrumple paper
How to uncrumple paper Binder reminder
Binder reminder Critical reminder
Critical reminder Adjectives for reminder
Adjectives for reminder Computation symbol
Computation symbol Pda
Pda Pda reminder 1
Pda reminder 1 Pda reminder 1
Pda reminder 1 As a quick reminder...adenine always pairs with
As a quick reminder...adenine always pairs with Thanks for the reminder.
Thanks for the reminder. Sql reminder
Sql reminder Parallel episode in flowers for algernon
Parallel episode in flowers for algernon Species tree
Species tree Foragry
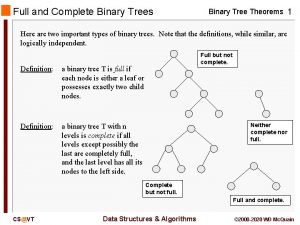
Foragry Definition of complete binary tree
Definition of complete binary tree Problem tree
Problem tree Difference between general tree and binary tree
Difference between general tree and binary tree Winner tree
Winner tree