Today Using separating planesaxes for collision testing Collision

Today • Using separating planes/axes for collision testing • Collision detection packages 12/4/2001 CS 638, Fall 2001

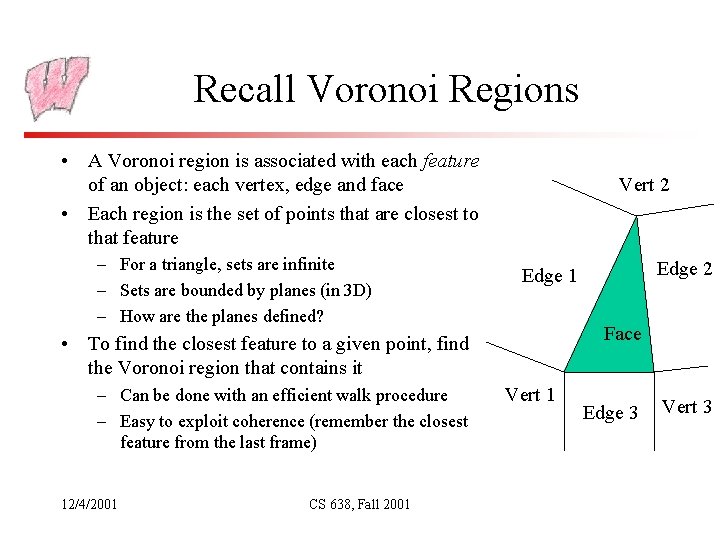
Recall Voronoi Regions • A Voronoi region is associated with each feature of an object: each vertex, edge and face • Each region is the set of points that are closest to that feature – For a triangle, sets are infinite – Sets are bounded by planes (in 3 D) – How are the planes defined? Vert 2 Face • To find the closest feature to a given point, find the Voronoi region that contains it – Can be done with an efficient walk procedure – Easy to exploit coherence (remember the closest feature from the last frame) 12/4/2001 CS 638, Fall 2001 Edge 2 Edge 1 Vert 1 Edge 3 Vert 3

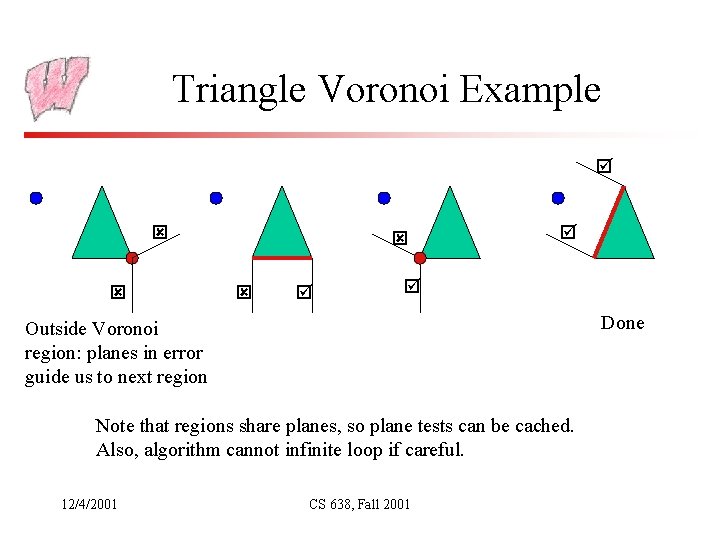
Triangle Voronoi Example Done Outside Voronoi region: planes in error guide us to next region Note that regions share planes, so plane tests can be cached. Also, algorithm cannot infinite loop if careful. 12/4/2001 CS 638, Fall 2001

Sphere-Box Testing • The Voronoi regions method works particularly well for boxes of various forms • The faces of the box cut space into 27 regions – Membership in each region can be defined by setting 6 bits, one for inside/outside each face plane – For AABB, test is even cheaper (inequalities) – Don’t even have to set all bits - some imply others • E. g Outside one face means inside the one opposite it • Determine which region the sphere’s center lies in • Each region has a closest feature, which will be the closest feature to the sphere • Note that k-dops also have a simple test of this form 12/4/2001 CS 638, Fall 2001

Sphere Test Hack • Expand objects out by the radius of the sphere, and test for point-insideobject using sphere’s center – Works well for player’s bounding sphere • This method is only worth it if the point-inside-object test is cheap • That means that the test is normally point-inside-plane for “expanded” face planes of the object • So, why is this method a hack? – Hint, think corners. What does the expanded shape look like at corners? • What form of test do you have to use to make the method accurate? 12/4/2001 CS 638, Fall 2001

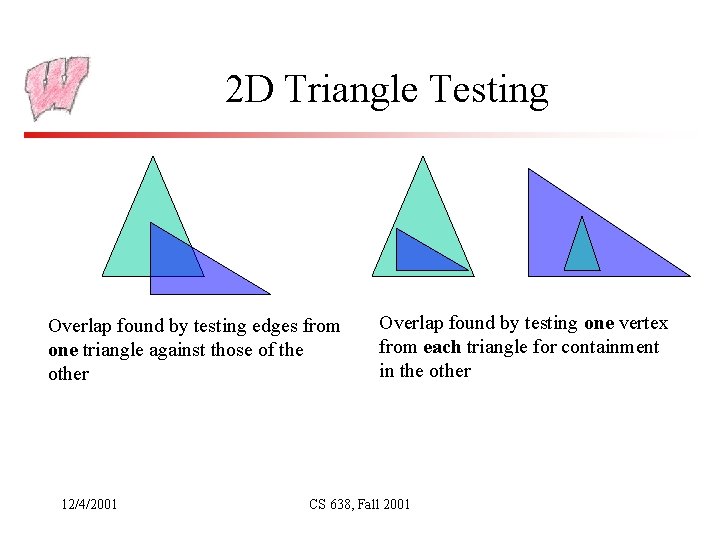
Triangle-Triangle Testing (Moller and Haines notes in reader) • Finding the intersection of two triangles is the base case for many general purpose collision packages • Observations: – Each triangle is a subset of the plane it lies in, so two triangles only intersect along the line where their plane’s intersect – Furthermore, they must overlap along the line of intersection of their planes – Hence, for two triangles to collide, each must intersect the plane of the other • Otherwise, they would have zero-size interval along the line of intersection • If the triangle planes are parallel, they can only intersect if they are coplanar, and then the problem is a 2 D one – Test edges of one triangle against those of the other – Then test for inclusion by testing one point from each triangle for containment in the other 12/4/2001 CS 638, Fall 2001

2 D Triangle Testing Overlap found by testing edges from one triangle against those of the other 12/4/2001 Overlap found by testing one vertex from each triangle for containment in the other CS 638, Fall 2001

Triangle-Triangle General Case (Moller and Haines notes in reader) • Option 1 (fastest or equal fastest): – Find points where triangle A’s edges intersect the plane of triangle B (at most 2 points) – no collision if no such points – Join them with a segment – Test segment against triangle B – test must check for containment – Version in book uses slow segment-triangle test, and doesn’t test containment • Option 2 (maybe equal fastest): – Find the line of intersection of the two planes – Find the intervals for which the lines lies inside each triangle (parameters only) – Test if the intervals overlap • Options 3 and 4: – Look for a separating plane, or use Voronoi regions 12/4/2001 CS 638, Fall 2001

Separating Planes • Two convex objects do not intersect if and only if there exists a plane that separates them - a separating plane • Can also use the separating axis - the normal of the separating plane – More convenient for testing • The number of potential separating plane orientations is finite for finitesided objects in 3 D – Must be parallel to one of the face planes from either object, or… – Must be simultaneously parallel to an edge from each object • Normal to the cross product of some pair of edges • In 2 D, separating lines must be parallel to an edge from one of the objects 12/4/2001 CS 638, Fall 2001

Using Separating Axes • Option 1: Use linear programming to find out if the point sets of the objects are linearly separable – Expensive, so not used • Option 2: Use a projection and interval tests – For each potential separating axis, find the extents of the triangle along that axis • In general case, same as projecting vertices onto a line and then taking max/min – Then look for overlap in the extents • This test is slower than necessary for triangles, but it works great for boxes, as we will see later 12/4/2001 CS 638, Fall 2001

Separating Axes Example This one separates 12/4/2001 This one doesn’t CS 638, Fall 2001

AABB-AABB • Two AABBs do not intersect if and only if • Can be seen as a series of separating axes tests – Three potential separating axes are the x, y and z axes – Each row checks for separation along one of the axes • There is also a positive version of the test, using “ands” – More like dimension reduction, which can be viewed as separating axis tests – Why use one over the other (in C++ at least)? 12/4/2001 CS 638, Fall 2001

OBB-OBB (Gottschalk, Lin, Manocha SIGGRAPH 96) • The fast OBB-OBB test uses separating axes – There are 15 possible axes for two OBBs: 3 faces from each box, and 3 x 3 edge direction combinations • The test projects the boxes onto each potential axis and looks for overlaps – Finding extents along the axis consists of some dot products and multiplications • Many optimizations make the test possible in about 200 operations – Express one box’s axes in terms of the other’s – Re-use common sub-expressions – Shortcut degenerate cases 12/4/2001 CS 638, Fall 2001

OBB Test 2 D test (3 D has three axes per box): a 2 a 1 T b 2 b 1 D • OBB consists of three axes and three “radii” along those axes • In all cases, assume that the separating axis in question has its origin at the center of one box • For separating axes derived from faces, we also know that the axis is parallel to one of the box axes – Express the other box’s axes in terms of the first box (a rotation) – Terms disappear 12/4/2001 CS 638, Fall 2001

Algorithms for 3 D Objects • OBB-Tree – A hierarchy of OBBs – Reports all collisions between triangle soup • Voronoi-Region Methods (Lin-Canny and V-Clip) – Only works for convex manifold objects, but extremely robust – Actually a closest features algorithm - gives closest features even if objects do not intersect 12/4/2001 CS 638, Fall 2001

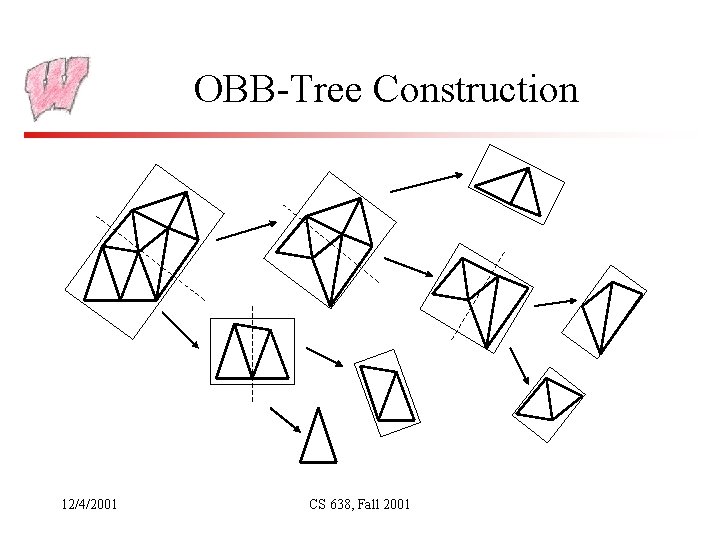
OBB-Trees (Gottschalk, Lin, Manocha: SIGGRAPH 96) • Represent an object (collection of triangles) with a hierarchy of OBBs – Leaves are triangles – Each box bounds its children • Do collision testing between two objects by doing collision testing between two trees – Test two boxes, one from each tree. If they intersect, recursively test 4 combinations of child boxes (binary trees) – Start with root boxes, base case is triangle-triangle tests – Result is a list of triangle pairs that intersect • Proof that a class project can go a long way 12/4/2001 CS 638, Fall 2001

Building the Trees • Assume the objects are rigid, so the tree is built as a preprocessing step • Tree is built top down: – Start with all the triangles, and put an OBB around them – Subdivide the box along the biggest dimension, classify triangles, and recurse on the two sets (just like building a BSP tree) – Child boxes don’t bear any specific relation to the parents – different orientations and sizes – Parents don’t even have to bound child boxes • Basic operation is fitting an OBB to a collection of triangles… 12/4/2001 CS 638, Fall 2001

OBB-Tree Construction 12/4/2001 CS 638, Fall 2001

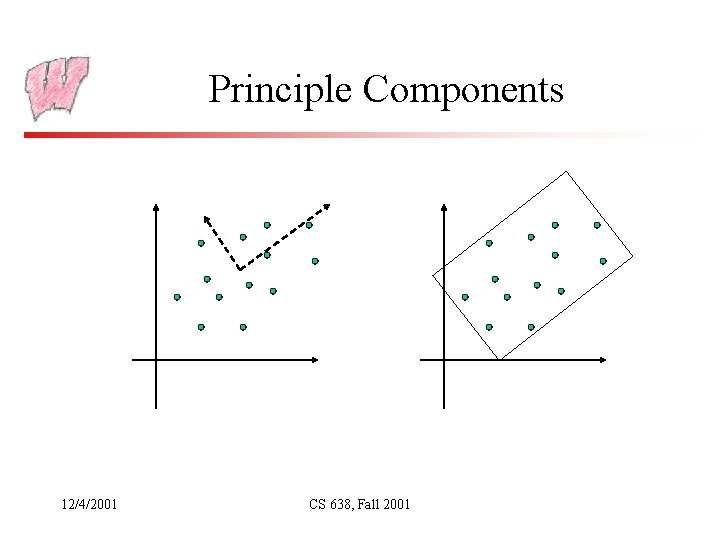
Fitting OBBs • The OBB fitting problem requires finding the orientation of the box that best fits the data • Ideally, you want the minimum volume for the box, but that’s hard • Instead, turn to an idea from statistics and AI (academic AI): principal components – – Point sample the convex hull of the geometry to be bound Find the mean and covariance matrix of the samples The mean will be the center of the box The eigenvectors of the covariance matrix are the principal directions – they are used for the axes of the box – The principle directions tend to align along the longest axis, then the next longest that is orthogonal, and then the other orthogonal axis 12/4/2001 CS 638, Fall 2001

Principle Components 12/4/2001 CS 638, Fall 2001

OBB-Tree Evaluation • OBB-Trees are the method of choice for unstructured geometry • Important analysis: Cost of detection, for two phases, is Nb. Cb+Nn. Cn – Number of broad tests times cost of broad test + number of narrow tests times cost of each narrow test – Cb and Nn depend on broad phases scheme – OBB-Tree is good at Nn and not bad at Cb, whereas AABB is good at Cb but not so good at Nn • Biggest way to improve it would be to exploit coherence, but it is not clear how to do so • Faster algorithms are restricted to more structured geometry … • Available as RAPID (just OBB-Trees) and V-COLLIDE (OBB-Trees and dimension reduction broad phase) 12/4/2001 CS 638, Fall 2001