Kinematics of collision processes 1 Introduction collision and

Kinematics of collision processes 1) Introduction – collision and decay processes 2) Rutherford scattering (Rutherford experiment from all sides). 3) Laws of energy and momentum conservation. 4) Laboratory and centre-of-mass frame. 5) Reaction energy, decay energy. 6) Collision diagram of momentum 7) Nonrelativistic, relativistic and ultrarelativistic approach. 8) Relativistic invariant kinematics variables. 9) Ultrarelativistic approach – rapidity 10) Transformation of kinematic quantities and cross sections from laboratory frame to centre-of-mass and vice versa

Introduction Study of collisions and decays of nuclei and elementary particles – main method of microscopic properties investigation. Elastic scattering – intrinsic state of motion of participated particles is not changed during scattering particles are not excited or deexcited and their rest masses are not changed. Inelastic scattering – intrinsic state of motion of particles changes (are excited), but particle transmutation is missing. Deep inelastic scattering – very strong particle excitation happens big transformation of the kinetic energy to excitation one. Nuclear reactions (reactions of elementary particles) – nuclear transmutation induced by external action. Change of structure of participated nuclei (particles) and also change of state of motion. Nuclear reactions are also scatterings. Nuclear reactions are possible to divide according to different criteria: According to history ( fission nuclear reactions, fusion reactions, nuclear transfer reactions …) According to collision participants (photonuclear reactions, heavy ion reactions, proton induced reactions, neutron production reactions …) According to reaction energy (exothermic, endothermic reactions) According to energy of impinging particles (low energy, high energy, relativistic collision, ultrarelativistic …)

Nuclear decay (radioactivity) – spontaneous (not always – induced decay) nuclear transmutation connected with particle production. Elementary particle decay - the same for elementary particles Set of masses, energies and moments of objects participating in the reaction or decay is named as process kinematics. Not all kinematics quantities are independent. Relations are determined by conservation laws. Energy conservation law and momentum conservation law are the most important for kinematics. Transformation between different coordinate systems and quantities, which are conserved during transformation (invariant variables) are important for kinematics quantities determination.

Rutherford scattering Target: thin foil from heavy nuclei (for example gold) Beam: collimated low energy α particles with velocity v = v 0 << c, after scattering v = vα << c The interaction character and object structure are not introduced Momentum conservation law: . . (1. 1) and so: …. . (1. 1 a) square: …. . (1. 1 b) Energy conservation law: (1. 2 a) and so: . . (1. 2 b) Using comparison of equations (1. 1 b) and (1. 2 b) we obtain: ………… (1. 3) For scalar product of two vectors it holds: so that we obtain:

If mt<<mα: Reminder of equation (1. 3) Left side of equation (1. 3) is positive → from right side results, that target and α particle are moving to the original direction after scattering → only small deviation of α particle If mt>>mα: Left side of equation (1. 3) is negative → large angle between α particle and reflected target nucleus results from right side → large scattering angle of α particle Concrete example of scattering on gold atom: mα 3. 7· 103 Me. V/c 2 , me 0. 51 Me. V/c 2 a m. Au 1. 8· 105 Me. V/c 2 1) If mt =me , then mt/mα 1. 4· 10 -4: Reminder of equation (1. 2 b): We obtain from equation (1. 3): ve = vt = 2 vαcos ≤ 2 vα We obtain from equation (1. 2 b): vα v 0 Then for magnitude of momentum it holds: meve = m (me/m ) ve ≤ m · 1. 4· 10 -4· 2 vα 2. 8· 10 -4 m v 0 Maximal momentum transferred to the electron is ≤ 2. 8· 10 -4 of original momentum and momentum of α particle decreases only for adequate (so negligible) part of momentum. Maximal angular deflection α of α particle arise, if whole change of electron and α momenta are to the vertical direction. Then ( α 0): α rad tan α = meve/m v 0 ≤ 2. 8· 10 -4 α ≤ 0. 016 o

Reminder of equation (1. 3) Reminder of equation (1. 2 b): 2) If mt =m. Au , then m. Au/mα 49 We obtain from equation (1. 3): v. Au = vt = 2(mα/mt)vα cos 2(mαvα)/mt We introduce this maximal possible velocity vt in (1. 2 b) and we obtain: vα v 0 because: Then for momentum is valid: m. Auv. Au ≤ 2 m vα 2 m v 0 Maximal momentum transferred on Au nucleus is double of original momentum and α particle can be backscattered with original magnitude of momentum (velocity). Maximal angular deflection α of α particle will be up to 180 o. Full agreement with Rutherford experiment and atomic model: 1) weakly scattered - scattering on electrons 2) scattered to large angles – scattering on massive nucleus Attention remember!!: we assumed that objects are point like and we didn't involve force character.

Inclusion of force character – central repulsive electric field: Thomson atomic model Electrons Thomson model – positive charged cloud with radius of atom RA : Electric field intensity outside: Electric field intensity inside: Positive charged cloud Rutherford atomic model Electrons The strongest field is on cloud surface and force acting on particle (Q = 2 e) is: This force decreases quickly with distance and it acts along trajectory L 2 RA t = L/ v 0 2 RA/ v 0. Resulting change of particle momentum = given transversal impulse: Maximal angle is: Positive charged nucleus Substituting RA 10 -10 m, v 0 107 m/s, Q = 79 e (Thomson model): rad tan 2. 7· 10 -4 → 0. 015 o only very small angles. Estimation for Rutherford model: Substituting RA = RJ 10 -14 m (only quantitative estimation): tan 2. 7 → 70 o also very large scattering angles.

Possibility of achievement of large deflections by multiple scattering Foil at experiment has 104 atomic layers. Let assume: 1) Thomson model (scattering on electrons or on positive charged cloud) 2) One scattering on every atomic layer 3) Mean value of one deflection magnitude 0. 01 o. Either on electron or on positive charged nucleus Mean value of whole magnitude of deflection after N scatterings is (deflections are to all directions, therefore we must use squares): …. (1) We deduce equation (1). Scattering takes place in space, but for simplicity we will show problem using two dimensional case: Deflections i are distributed both in positive and negative directions statistically around Gaussian normal distribution for studied case. So that mean value of particle deflection from original direction is equal zero: Multiple particle scattering

the same type of scattering on each atomic layer: Then we can derive given relation (1): Because it is valid for two inter-independent random quantities a and b with Gaussian distribution: And already showed relation is valid: We substitute N by mentioned 104 and mean value of one deflection = 0. 01 o. Mean value of deflection magnitude after multiple scattering in Geiger and Marsden experiment is around 1 o. This value is near to the real measured experimental value. Certain very small ratio of particles was deflected more then 90 o during experiment (one particle from every 8000 particles). We determine probability P( ), that deflection larger then originates from multiple scattering. If all deflections will be in the same direction and will have mean value, final angle will be ~100 o (we accent assumption each scattering has deflection value equal to the mean value). Probability of this is P = (1/2)N =(1/2)10000 = 10 -3010. Proper calculation will give: We substitute: Clear contradiction with experiment – Thomson model must be rejected

Derivation of Rutherford equation for scattering: Assumptions: 1) particle and atomic nucleus are point like masses and charges. 2) Particle and nucleus experience only electric repulsion force – dynamics is included. 3) Nucleus is very massive comparable to the particle and it is not moving. Acting force: Charged particle with the charge Ze produces a Coulomb potential: Two charged particles with the charges Ze and Z‘e and the distance experience a Coulomb force giving rice to a potential energy : Coulomb force is: 1) Conservative force – force is gradient of potential energy: 2) Central force: Magnitude of Coulomb force is and force acts in the direction of particle join. Electrostatic force is thus proportional to 1/r 2 trajectory of particle is a hyperbola with nucleus in its external focus.

We define: Impact parameter b – minimal distance on which particle comes near to the nucleus in the case without force acting. Scattering angle - angle between asymptotic directions of particle arrival and departure. First we find relation between b and : Nucleus gives to the particle impulse particle momentum changes from original value p 0 to final value p : …………. (1) Using assumption about target fixation we obtain that kinetic energy and magnitude of particle momentum before, during and after scattering are the same: p 0 = p = m v 0=m v Geometry of Rutheford scattering. We see from figure: ………. . (2) Because impulse is in the same direction as the change of momentum, it is valid: …………… (3) Momenta in Rutheford scattering: where is running angle between and along particle trajectory.

…………. . . . . ……(4) We substitute (2) and (3) to (1): We change integration variable from t to : …. (5) where d dt is angular velocity of particle motion around nucleus. Electrostatic action of nucleus on particle is in direction of the join vector force momentum do not act angular momentum is not changing (its original value is m v 0 b) and it is connected with angular velocity = d /dt m r 2 = const = m r 2 (d /dt) = m v 0 b then: we substitute dt/d at (5): . . . . … (6) We substitute electrostatic force F (Z =2): We obtain: because it is valid: We substitute to the relation (6): Scattering angle is connected with collision parameter b by relation: The smaller impact parameter b the larger scattering angle . … (7)

Energy and momentum conservation law Just these conservation laws are very important. They determine relations between kinematic quantities. It is valid for isolated system: Conservation law of whole energy: Nonrelativistic approximation (m 0 c 2 >> EKIN): EKIN = p 2/(2 m 0) Together it is valid for elastic scattering: Ultrarelativistic approximation (m 0 c 2 << EKIN): E ≈ EKIN ≈ pc Conservation law of whole momentum:

We obtain for elastic scattering: Using momentum conservation law: and We obtain using cosine theorem: Nonrelativistic approximation: Using energy conservation law: We can eliminated two variables using these equations. The energy of reflected target particle E‘KIN 2 and reflection angle ψ are usually not measured. We obtain relation between remaining kinematic variables using given equations: Ultrarelativistic approximation: Using energy conservation law: We obtain using this relation and momentum conservation law: cos 1 and therefore: 0

Laboratory and centre-of-mass system We are studying not only collisions of particle with fixed centre. Also the description of more complicated case can be simplified by separation of the centre-of-mass motion in the case of central potential. We solve problem using advantageous coordinate system. Laboratory system – experiment is running in this system, all kinematic quantities are measured in this system. It is primary from the side of experiment. Target particle is mostly in the rest in this coordinate system (Experiments with colliding beams are exception). Centre-of-mass system – centre-of-mass is in this system in the rest and hence total momentum of all particles is zero. Mostly we are interested in relative motion of particles and no motion of system as whole using of such coordinate system is very useful. Remainder of centre-of-mass installation: we assumed two particles (with masses m 1, m 2 and positions ) interacting mutually only by central potential : Equations of motion can be written in form: …………(1) coordinate origin where has in spherical coordinates form ( are appropriate unit vectors): i = 1, 2

Potential energy depends only on relative distance of particles. We define new coordinates: Reminder of equations (1): ……………. (2) Using relations (1) and (2) we obtain (it is valid ): where is the reduced and M the total masses of the system. In the case of central potential motion can be split by rewritten to relative distance and centre-of-mass coordinates: Centre-of-mass motion is uniform and straightforward, centre-of-mass moves in the laboratory with a constant velocity independently of specific form of the potential. The dynamics is completely contained in the motion of a fictitious particle with the reduced mass and coordinate r. In the centre-of-mass system, the complete dynamics is described by the motion of single particle, with the mass , scattered by fixed central potential. Kinetic energy splits into kinetic energy of centre-of-mass and into the part corresponding to relative particle motion (kinetic energy in centre-of-mass system).

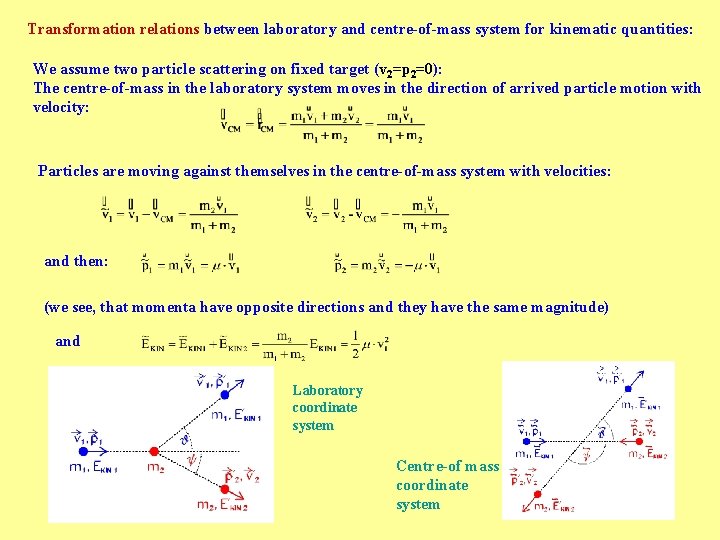
Transformation relations between laboratory and centre-of-mass system for kinematic quantities: We assume two particle scattering on fixed target (v 2=p 2=0): The centre-of-mass in the laboratory system moves in the direction of arrived particle motion with velocity: Particles are moving against themselves in the centre-of-mass system with velocities: and then: (we see, that momenta have opposite directions and they have the same magnitude) and Laboratory coordinate system Centre-of mass coordinate system

Laboratory coordinate system Centre-of-mass coordinate system Derivation of relation between scattering angles in centre-of-mass and laboratory coordinate systems: Relation between velocity components in direction of beam particle motion is: Relation between velocity components perpendicular to the direction of beam particle motion: We divide these relations: . . . …………. . (3) It is valid for elastic scattering: We rewrite equation (3) to the form:

Reaction energy, decay energy Up to now we studied only elastic scattering. To extend our analysis on other reaction types (decays, nuclear reactions or particle creations), we introduce: Reaction energy Q: is defined as difference of sums of rest particle energies before reaction and after reaction or as difference of sums kinetic energies after reaction and before it: Value of Q is independent on coordinate system. (Reminder: m indicates rest mass): Exothermic reactions Q 0 energy is released (spontaneous decays of nuclei or particles, reactions are realized for any energy of arrived particle). We are talking about decay energy in such case. Elastic scattering Q = 0 Endothermic reactions Q 0 energy must be delivered (reaction is not proceed spontaneously, it is necessary certain threshold energy of arrived particle to realize reaction). Threshold energy in centre-of-mass coordinate system: Using definition of centre-of-mass system we obtain for beginning state: We obtain from momentum conservation law: It is possible case, that all end particles have zero momentum and thus also their individual kinetic energies are zero: Thus threshold energy ETHR in centre -of-mass coordinate system is:

Threshold energy in laboratory system: Usually we need to know reaction threshold in laboratory system. We assume nonrelativistic reaction of two particles with rest masses m 1 a m 2. The target particle is in the rest in the laboratory system. Centre-of-mass is moving in the laboratory system, it has momentum p 1 and equivalent kinetic energy: this energy is not usable for reaction. That means threshold energy must be: From definition ETHR is minimal EKIN 1: Substituting p 12 into previous equation: Case m 1 << m 2 leads to ETHR = |Q| Relation between reaction energy and kinematic variables of arrived and scattered particle can be written (we use the same procedure as for similar relation for elastic scattering): We often need relation: Solution is: EKIN 3 =f(EKIN 1, ), we define x √E‘KIN 3 where and Inelastic scattering is always endothermic (where M 0 i M 0 f, Ei. KIN, Ef. KIN are total sums): M 0 i M 0 f Ei. KIN Ef. KIN Q 0 Decay of particle at rest: Q = m 0 ic 2 -M 0 fc 2. Momenta of particles after two-particle decay have the same magnitude but opposite direction. Isotropic distribution. Momenta of products:

Collision momentum diagram We assumed again, that target nucleus is in the rest and no relativistic approximation. We write relations between momenta of particles before and after collision: (We obtain law of momentum conservation for studied case by sum of these equations: ) Such relations are initial equations for construction of vector diagram of momenta: 1) Momentum of impinging particle we represent by oriented abscissa . 2) We divide abscissa to two parts in the proportion 3) We describe circle around the point O passing through the point C. The circle radius is equal to magnitude of momenta p 1 in the centre-of-mass system . The circle geometrical place of vertexes B of vector triangle of momenta ABC (represents law of momentum conversation), which sides and represent possible momenta of particles after collision in the laboratory system. m 1 < m 2 : m 1 = m 2 : m 1 > m 2 :

The point A can be inside given circle, on it or outside dependent on ratio of particle masses. A scattering angle in centre-of-mass system can take all possible values from 0 do . Allowed values of scattering angle in the laboratory system and reflection angle in the laboratory system are in the table: m 1 < m 2 : m 1 m 2 m 1 = m 2 m 1 m 2 v 1 > v. CM v 1 = v. CM v 1 < v. CM + /2 + = /2 + /2 = <0, > = <0, /2> = <0, MAX > = <0, /2> m 1 = m 2 : m 1 > m 2 : m 1 < m 2 impinging particles are scattered to both hemispheres m 1 = m 2 impinging particles are scattered to front hemisphere In the laboratory system: m 1 > m 2 impinging particles are scattered to front hemisphere to cone with top angle 2 MAX (direction of impinging particles is axe of cone): sin MAX =m 2/m 1 Relation between scattering angle and reflection angle in the laboratory and the centre-of-mass system (remainder of elastic scattering assumption): Vector momentum diagram provides full information given by conservation laws of energy and momentum. It shows possible variants of particle fly away but it has no information about probabilities of realisation of particular possible variants.

Relativistic description – nonrelativistic and ultrarelativistic approximations Total energy is connected with momentum by relativistic relation: We label rest mass m m 0. Rest masses and rest energies are invariant under Lorentz transformation (they are the same in all inertial coordinate systems) and then invariant is also quantity (optimal coordinate system can be chose for its calculation): It is valid not only for single particle but also for particle system in the given time: . . . (1) We express kinetic energy and momentum: Threshold energy in centre-of-mass system leads to zero sum of kinetic energies of system in ending state. We express invariant (1) for beginning state of system in laboratory and for ending state in centre-of-mass systems: We substitute p 2: and EKIN 1:

We express EKIN 1: We obtain: Because: we obtain In no relativistic approximation (Q<<m 2 c 2) we obtain known relation. In ultrarelativistic approximation (Q>>m 1 c 2 a Q>>m 2 c 2): ETHR = Q 2

Relativistic relation between scattering angle in centre-of-mass and laboratory system Lorentz transformation of momenta and energy from centre-of-mass system to laboratory system is (centre-of-mass moves to the direction of axis y): We use polar coordinate system: and We derived relation for angle : In nonrelativistic approximation, where v. CM << c we obtain known relation, which we already derived.

In common practice, kinetic energy of impinging particle is used instead centre-of-mass velocity: Centre-of-mass velocity in the laboratory system is given by ratio between total momentum and total energy of the system in the laboratory system: We use relation between kinetic energy and momentum: We obtain: This relation can be substitute to the relation for scattering angle. We will show special case, when scattering angle in the centre-of-mass system is π/2: In ultrarelativistic approximation (EKIN 1 >> m 1 c 2 and EKIN 1 >> m 2 c 2) we obtain: In the laboratory system, particles are produced to the very small angle.

Relativistic invariant variables We can obtain velocity of centre-of-mass during scattering of two particles with the rest masses m 1 and m 2 by total relativistic momentum and total relativistic energy: (1. a) m 1 refers to the projectile mass and m 2 to target mass. We use laboratory kinematic variables and we obtain: …………… (1. b) Nonrelativistic approximation (m 1 c 2 p 1 c): ……………. . (1. c) Ultrarelativistic approximation (m 1 c 2 p 1 c a m 2 c 2 p 1 c): For m 1 m 2: and We obtain general relativistic relation for CM : So that (m 12 c 4 = E 12 -p 12 c 2): using equation (1. b):

and we obtain … (2) Equation is reduced for limits E 1 p 1 c m 1 c 2 and p 1 c m 2 c 2 to formerly given ultrarelativistic limit: Quantity in the divisor (2) is invariant scalar. We prove this using the square of following four-vector in the laboratory frame (p 2 = 0): This scalar has the same value in arbitrary reference frame. It has simple interpretation in the centre -of-mass reference frame (total momentum in this reference frame is zero): and s is square of total energy accessible in centre-of-mass system. Then Invariant variable s is often used for description of high-energy collisions. The quantity s is very useful in the case of colliders. Invariant variable t is also often used – square of the four-momentum transfer in a collision (square of the difference in the energy-momentum four-vectors of the projectile before and after scattering): …………. (3 a)

Energy and momentum conservation laws are valid and we can express t also in target variables: ………………. . (3 b) variable t is invariant and it can be calculated in arbitrary coordinate system. We add yet variable u: or Variables t, u and s are named as Lorentz invariant Mandelstam variables, which sum generally satisfy equation: In the case of elastic scattering in the centre-of-mass system (for both particles and ) Because – 1 ≤ cos ≤ 1 it is valid t 0. Using (3 a, b) we can look on variable t as on mass-square of exchanged particle (with energy and momentum ). Imaginary mass virtual particle. Such diagrams were pioneered by R. Feynman in the calculation of scattering amplitudes in QED and they are referred to as Feynman graphs. Let us define a variable q 2 ( q 2 c 2 = -t ), which is equal to square of momentum transferred to target nucleus q 2 (m 2 v 2)2 in no relativistic approximation. Feynman graph:

Ultrarelativistic approximation -rapidity In high-energy physics (ultrarelativistic collisions velocity of beam particles v c) new kinematic variable – rapidity – is useful to introduce (usually we have c=1, m is total mass): We choose beam direction as axe z, thus we can write total energy and momentum of particle as: E = m. Tc 2 cosh y, px, py a pz = m. Tc sinh y Reminder: We introduced transversal mass m. T : and rapidity y: and thus: For nonrelativistic limit (β → 0): y = β ( ) For ultrarelativistic limit (β → 1): y → ∞ Rapidity using leads to very simple transformation from one coordinate system to another: where y 21 is rapidity of the coordinate system 2 in the system 1. Thus we write for transformation from the laboratory to the centre-of-mass systems : Examples: GSI Darmstadt ( ELAB = 1 Ge. V/A y=0. 458 β=0. 875 ) SPS CERN ( ELAB = 200 Ge. V/A y=6. 0 β=1. 000 ) Relation between transversal LHC CERN ( ELAB=3500+3500 Ge. V/A y=17. 8 β=1. 000 ) component of velocity and rapidity