The Padding Argument Complexity 1 Motivation ScalingUp Complexity

Motivation: Scaling-Up Complexity Claims We have: space can be simulated by… + non-determinism space

Formally si(n) can be computed with space si(n) Claim: For any two space constructible

Padding argument • Let L NPSPACE(s 1(f(n))) • There is a 3 -Tape-NTM ML:

Padding argument • Let L’ = { x 0 f(|x|)-|x| | x L }

Padding argument – ML’ In O(log(f(|x|)) space 1. Count backwards the number of 0’s

Padding argument Total space: O(s 1(f(|x|))) f(|x|) Input babba 0000000000000000 �� Work �� O(s

Padding Argument • • Complexity We started with L NSPACE(s 1(f(n))) We showed: L’

Padding Argument • The DTM for L’ will simulate the DTM for L when

Padding Argument • When the input head leaves the input part, just pretend it

Savitch: Generalized Version Theorem (Savitch): S(n) ≥ log(n) NSPACE(S(n)) SPACE(S(n)2) Proof: We proved NL

Corollary: PSPACE = NPSPACE Proof: Clearly, PSPACE NPSPACE. By Savitch’s theorem, NPSPACE. Complexity 13

Slides: 13

Download presentation

The Padding Argument Complexity 1

Motivation: Scaling-Up Complexity Claims We have: space can be simulated by… + non-determinism space + determinism We want: space + non-determinism Complexity can be simulated by… space + determinism 2

Formally si(n) can be computed with space si(n) Claim: For any two space constructible functions s 1(n), s 2(n) logn, f(n) n: simulation overhead NSPACE(s 1(n)) SPACE(s 2(n)) NSPACE(s 1(f(n))) SPACE(s 2(f(n))) E. g NSPACE(n) SPACE(n 2) NSPACE(n 2) SPACE(n 4) Complexity 3

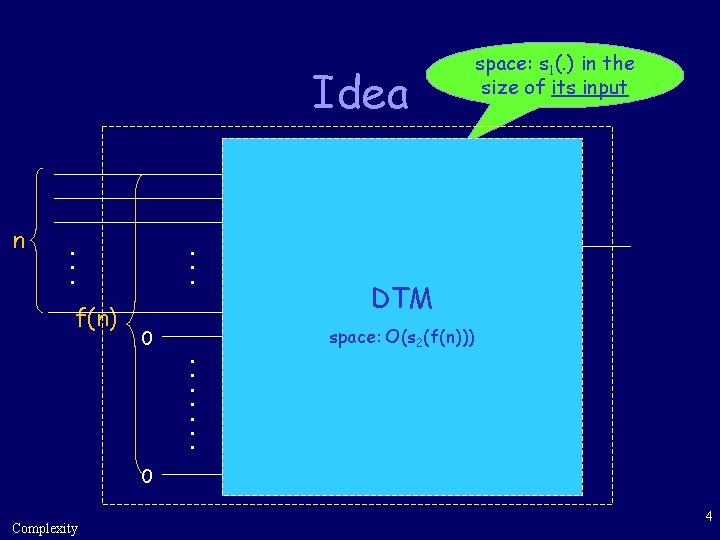
Idea n . . . f(n) . . . 0 . . . . n . . . space: s 1(. ) in the size of its input NTM space: DTM O(s 1(f(n))) space: O(s 2(f(n))) 0 Complexity 4

Padding argument • Let L NPSPACE(s 1(f(n))) • There is a 3 -Tape-NTM ML: |x| Input babba �� Work �� Complexity O(s 1(f(|x|))) 5

Padding argument • Let L’ = { x 0 f(|x|)-|x| | x L } • We’ll show a NTM ML’ which decides L’ in the same number of cells as ML. f(|x|) Input babba 0000000000000000 �� Work �� Complexity O(s 1(f(|x|)) 6

Padding argument – ML’ In O(log(f(|x|)) space 1. Count backwards the number of 0’s and check there are f(|x|)-|x| such. in O(s (f(|x|))) space 1 2. Run ML on x. f(|x|) Input babba 0000000000000000 �� Work �� Complexity O(s 1(f(|x|))) 7

Padding argument Total space: O(s 1(f(|x|))) f(|x|) Input babba 0000000000000000 �� Work �� O(s 1(f(|x|))) Complexity 8

Padding Argument • • Complexity We started with L NSPACE(s 1(f(n))) We showed: L’ NSPACE(s 1(n)) Thus, L’ SPACE(s 2(n)) Using the DTM for L’ we’ll construct a DTM for L, which will work in O(s 2(f(n))) space. 9

Padding Argument • The DTM for L’ will simulate the DTM for L when working on its input concatenated with zeros Input babba �� 000000000000 Complexity 10

Padding Argument • When the input head leaves the input part, just pretend it encounters 0 s. • keeping track after the simulated position takes O(log(f(|x|))) space. • Thus our machine uses O(s 2(f(|x|))) space. • NSPACE(s 1(f(n))) SPACE(s 2(f(n))) Complexity 11

Savitch: Generalized Version Theorem (Savitch): S(n) ≥ log(n) NSPACE(S(n)) SPACE(S(n)2) Proof: We proved NL SPACE(log 2 n). The theorem follows from the padding argument. Complexity 12

Corollary: PSPACE = NPSPACE Proof: Clearly, PSPACE NPSPACE. By Savitch’s theorem, NPSPACE. Complexity 13