Synchronization in Coupled Chaotic Oscillators SangYoon Kim Department

![Chaos and Synchronization Lorenz Attractor [Lorenz, J. Atmos. Sci. 20, 130 (1963). ] z Chaos and Synchronization Lorenz Attractor [Lorenz, J. Atmos. Sci. 20, 130 (1963). ] z](https://slidetodoc.com/presentation_image/afc174d4ae9a03aff6832c8c00a1b8b5/image-2.jpg)



![Noise Effect on the Chaos Synchronization Strong Synchronization [Small Noise Small Effect] All UPOs Noise Effect on the Chaos Synchronization Strong Synchronization [Small Noise Small Effect] All UPOs](https://slidetodoc.com/presentation_image/afc174d4ae9a03aff6832c8c00a1b8b5/image-11.jpg)







- Slides: 23

Synchronization in Coupled Chaotic Oscillators Sang-Yoon Kim Department of Physics Kangwon National University Korea Synchronization in Coupled Periodic Oscillators Synchronous Pendulum Clocks Synchronously Flashing Fireflies 1
![Chaos and Synchronization Lorenz Attractor Lorenz J Atmos Sci 20 130 1963 z Chaos and Synchronization Lorenz Attractor [Lorenz, J. Atmos. Sci. 20, 130 (1963). ] z](https://slidetodoc.com/presentation_image/afc174d4ae9a03aff6832c8c00a1b8b5/image-2.jpg)
Chaos and Synchronization Lorenz Attractor [Lorenz, J. Atmos. Sci. 20, 130 (1963). ] z Butterfly Effect: Sensitive Dependence on Initial Conditions [Small Cause Large Effect] y x Coupled Chaotic (Chemical) Oscillators [H. Fujisaka and T. Yamada, Prog. Theor. Phys. 69, 32 (1983). ] • Other Pioneering Works A. S. Pikovsky, Z. Phys. B 50, 149 (1984). • V. S. Afraimovich, N. N. Verichev, and M. I. Rabinovich, Radiophys. Quantum Electron. 29, 795 (1986). • L. M. Pecora and T. L. Carrol, Phys. Rev. Lett. 64, 821 (1990). • 2

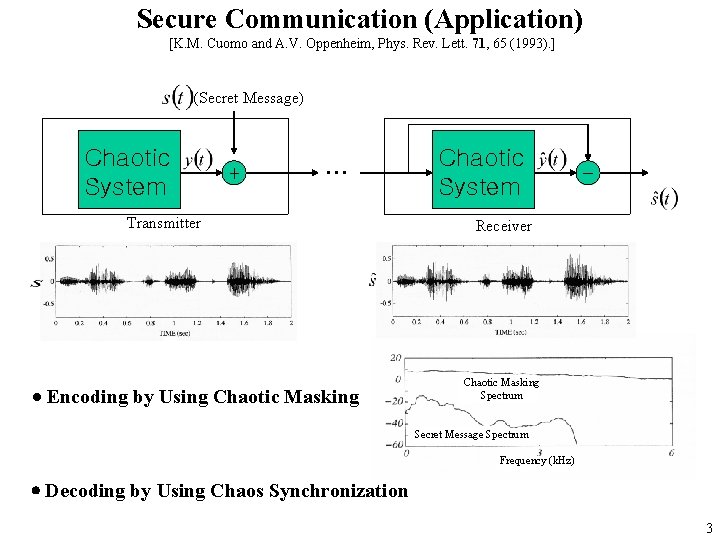
Secure Communication (Application) [K. M. Cuomo and A. V. Oppenheim, Phys. Rev. Lett. 71, 65 (1993). ] (Secret Message) Chaotic System + Transmitter Encoding by Using Chaotic Masking Chaotic System - Receiver Chaotic Masking Spectrum Secret Message Spectrum Frequency (k. Hz) Decoding by Using Chaos Synchronization 3

Several Types of Chaos Synchronization Different degrees of correlation between the interacting subsystems Identical Subsystems Complete Synchronization [H. Fujisaka and T. Yamada, Prog. Theor. Phys. 69, 32 (1983). ] Nonidentical Subsystems • Generalized Synchronization [N. F. Rulkov et. al. , Phys. Rev. E 51, 980 (1995). ] • Phase Synchronization [M. Rosenblum, A. S. Pikovsky, and J. Kurths, Phys. Rev. Lett 76, 1804 (1996). ] • Lag Synchronization [M. Rosenblum, A. S. Pikovsky, and J. Kurths, Phys. Rev. Lett 78, 4193 (1997). ] 4

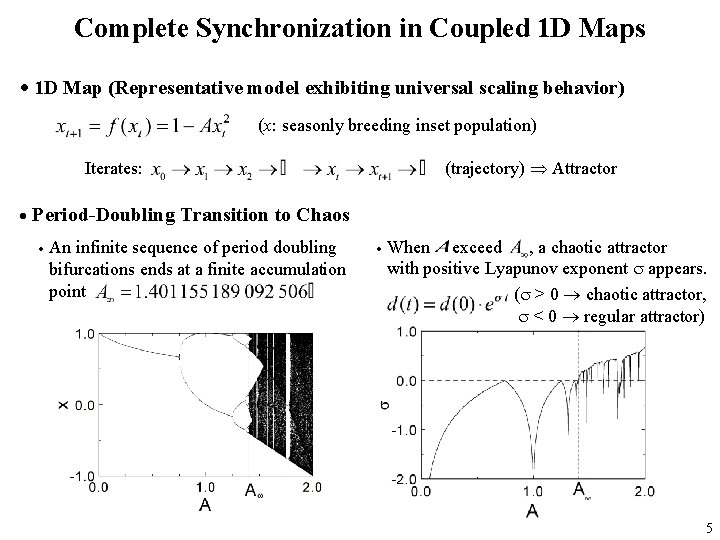
Complete Synchronization in Coupled 1 D Maps 1 D Map (Representative model exhibiting universal scaling behavior) (x: seasonly breeding inset population) (trajectory) Attractor Iterates: Period-Doubling Transition to Chaos An infinite sequence of period doubling bifurcations ends at a finite accumulation point When exceed , a chaotic attractor with positive Lyapunov exponent appears. ( > 0 chaotic attractor, < 0 regular attractor) 5

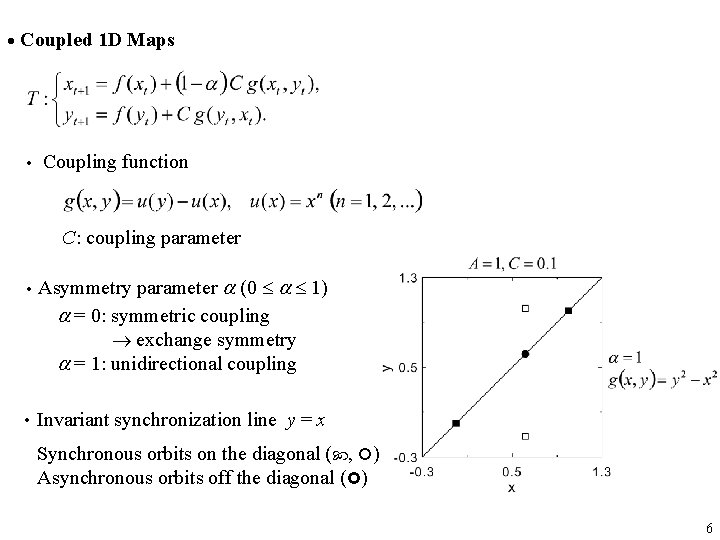
Coupled 1 D Maps Coupling function C: coupling parameter Asymmetry parameter (0 1) = 0: symmetric coupling exchange symmetry = 1: unidirectional coupling Invariant synchronization line y = x Synchronous orbits on the diagonal ( , ) Asynchronous orbits off the diagonal ( ) 6

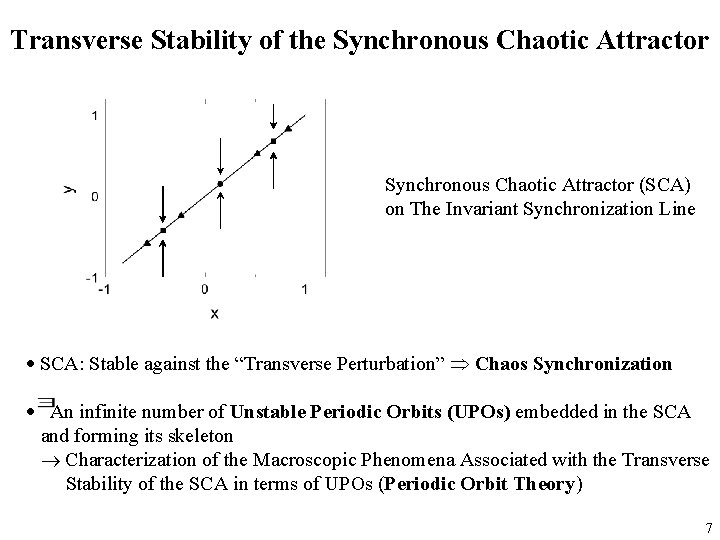
Transverse Stability of the Synchronous Chaotic Attractor (SCA) on The Invariant Synchronization Line SCA: Stable against the “Transverse Perturbation” Chaos Synchronization An infinite number of Unstable Periodic Orbits (UPOs) embedded in the SCA and forming its skeleton Characterization of the Macroscopic Phenomena Associated with the Transverse Stability of the SCA in terms of UPOs (Periodic Orbit Theory) 7

Competition between Periodic Saddles and Repellers Investigation of Transverse Stability of the SCA in Terms of UPOs ( : transverse Lyapunov exponent of the SCA) {UPOs} = {Transversely Stable Periodic Saddles (PSs)} + {Transversely Unstable Periodic Repellers (PRs)} “Strength” of {PSs} > “Strength” of {PRs} < 0 (SCA: transversely stable) Chaos Synchronization “Strength” of {PSs} < “Strength” of {PRs} > 0 (SCA: transversely unstable chaotic saddle) Complete Desynchronization Chaos Synchronization Blow-out Bifurcation C 8

Chaotic Synchronization in Unidirectionally Coupled 1 D Maps c: Coupling Parameter, : Noise Strength (i) (i=1, 2): Uniform Random Variable with and Phase Diagram ( =0) • Appearance of a Synchronous Chaotic Attractor (SCA) on the Invariant Diagonal when Passing a Critical Line (heavy solid line). a=1. 82 • an Infinite Number of UPOs inside the SCA. a =1. 401 155 … • Strong Synchronization (Hatched Region, <0) All Sync. UPOs: Transversely Stable Periodic Saddles No Bursting • Weak Synchronization (Gray and Dark Gray Regions, <0) {Sync. UPOs} = {Periodic Saddles (PSs)} + {Periodic Repellers (PRs)} {PSs}: Dominant SCA: Transversely Stable ( <0), {PRs} Local Bursting 9

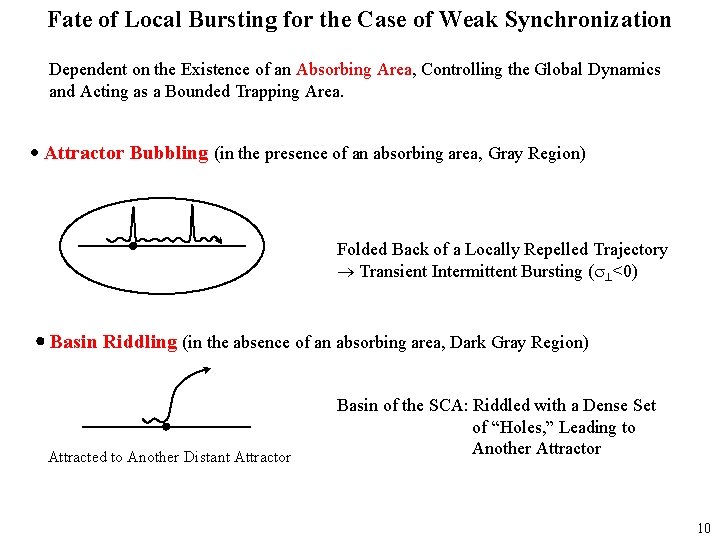
Fate of Local Bursting for the Case of Weak Synchronization Dependent on the Existence of an Absorbing Area, Controlling the Global Dynamics and Acting as a Bounded Trapping Area. Attractor Bubbling (in the presence of an absorbing area, Gray Region) Folded Back of a Locally Repelled Trajectory Transient Intermittent Bursting ( <0) Basin Riddling (in the absence of an absorbing area, Dark Gray Region) Attracted to Another Distant Attractor Basin of the SCA: Riddled with a Dense Set of “Holes, ” Leading to Another Attractor 10
![Noise Effect on the Chaos Synchronization Strong Synchronization Small Noise Small Effect All UPOs Noise Effect on the Chaos Synchronization Strong Synchronization [Small Noise Small Effect] All UPOs](https://slidetodoc.com/presentation_image/afc174d4ae9a03aff6832c8c00a1b8b5/image-11.jpg)
Noise Effect on the Chaos Synchronization Strong Synchronization [Small Noise Small Effect] All UPOs (embedded in the SCA): Transversely Stable No Noise Sensitivity Slightly Perturbed SCA ( Noise Strength) Evolution of Transverse Variable un (=xn-yn) vs. n a=1. 82 c=-1. 5 =0. 0005 Weak Synchronization [Small Noise Large Effect] Local Transverse Repulsion of Periodic Repellers Noise Sensitivity • Bubbling Transient Intermittent Bursting ( =0) Persistent Intermittent Bursting of the Bubbling Attractor Filling an Absorbing Area for Any Small Noise. a=1. 82 c=-0. 7 =0. 0005 • Riddling SCA ( =0)with a Basin (Gray) Riddled with a Dense Set of “Holes, ” Leading to Divergent Orbits (White) Chaotic Transient (Black) with a Finite Lifetime. a=1. 82, c=-2. 91 =0. 0005 11

Quantitative Characterization of the Noise Sensitivity of the SCA [S. -Y. Kim, W. Lim, A. Jalnine, and S. P. Kuznetsov, Phys. Rev. E 67, 016217 (2003); A. Jalnine and S. -Y. Kim, Phys. Rev. E 65, 026210 (2002); S. -Y. Kim, W. Lim, and Y. Kim, Prog. Theor. Phys. 107, 239 -252 (2002). ] Noise Sensitivity Induced by Local Transverse Repulsion of Periodic Repellers Embedded in the Weakly Stable SCA A Typical Trajectory may Have Segments of Arbitrarily Long Length M with Positive Local (M-Time) Transverse Lyapunov Exponents M The Weakly-Stable SCA for =0 Becomes Sensitive with respect to Any Small Noise Strength . Characterization of Noise Sensitivity • Measured by Calculating a Derivative of the Transverse Variable un (=xn-yn) with respect to the Noise Strength along a Synchronous Trajectory R N-k ( x *k ) R M ( x *k ) : Local (M-time) Transverse Stability Multiplier, = exp(M M ) : Local (M-time) Transverse Lyapunov exponent : Synchronous Orbit for =0, 12

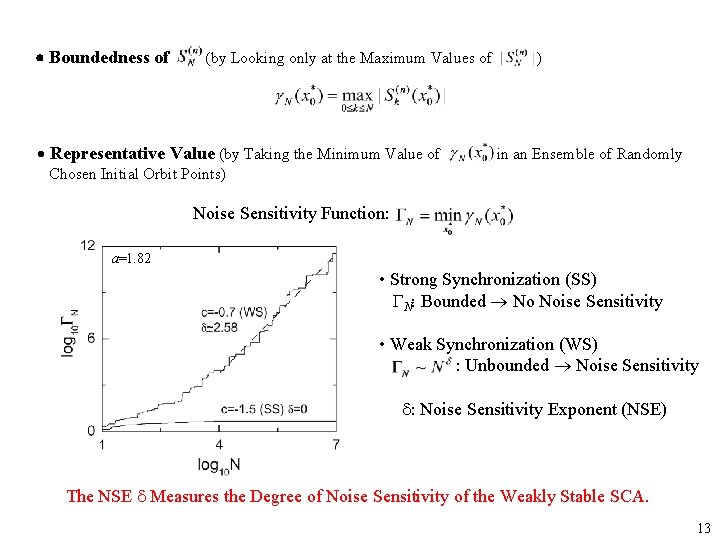
Boundedness of (by Looking only at the Maximum Values of Representative Value (by Taking the Minimum Value of ) in an Ensemble of Randomly Chosen Initial Orbit Points) Noise Sensitivity Function: a=1. 82 • Strong Synchronization (SS) N: Bounded No Noise Sensitivity • Weak Synchronization (WS) : Unbounded Noise Sensitivity : Noise Sensitivity Exponent (NSE) The NSE Measures the Degree of Noise Sensitivity of the Weakly Stable SCA. 13

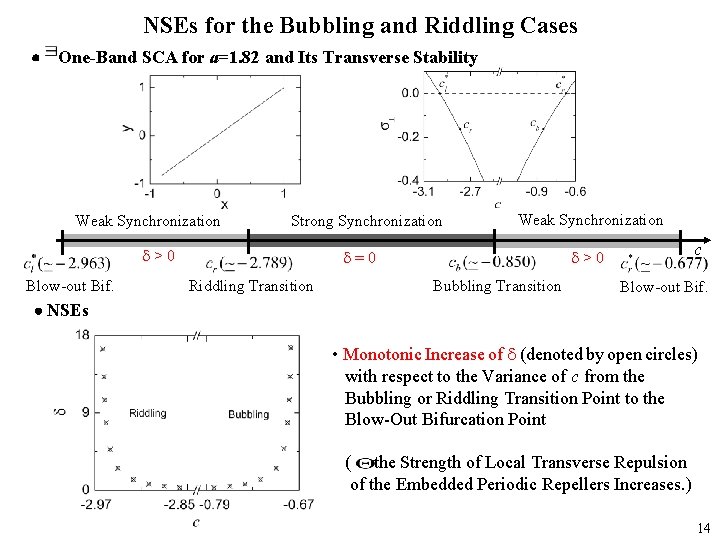
NSEs for the Bubbling and Riddling Cases One-Band SCA for a=1. 82 and Its Transverse Stability Weak Synchronization Strong Synchronization >0 Blow-out Bif. Weak Synchronization =0 Riddling Transition c >0 Bubbling Transition Blow-out Bif. NSEs • Monotonic Increase of (denoted by open circles) with respect to the Variance of c from the Bubbling or Riddling Transition Point to the Blow-Out Bifurcation Point ( the Strength of Local Transverse Repulsion of the Embedded Periodic Repellers Increases. ) 14

Parameter-Mismatching Effect on the Weak Synchronization Coupled Non-Identical 1 D Maps : Mismatching Parameter Comparison of the Parameter-Sensitivity Case with the Noise-Sensitivity Case • Parameter Sensitivity R N-k ( x *k ) [ fa(x) = -x 2: Bounded Chaotic Signal ] • Noise Sensitivity R N-k ( x *k ) [ : Bounded Random Variable] Growth of for Large N must be Determined by the Local Transverse Stability Multipliers RM, as in the Noise-Sensitivity Case. N ~ N for both the Parameter-Mismatching and Noise Cases: Parameter Sensitivity Exponent (PSE) (crosses) = NSE (open circles) 15

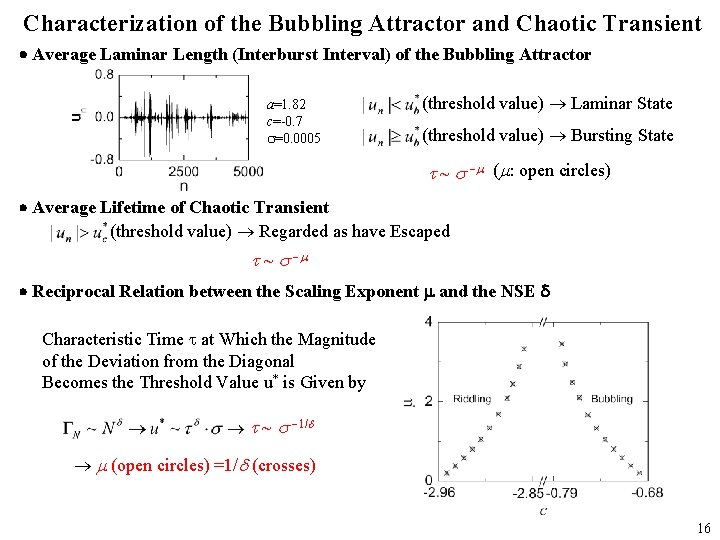
Characterization of the Bubbling Attractor and Chaotic Transient Average Laminar Length (Interburst Interval) of the Bubbling Attractor a=1. 82 c=-0. 7 =0. 0005 (threshold value) Laminar State (threshold value) Bursting State ~ - ( : open circles) Average Lifetime of Chaotic Transient (threshold value) Regarded as have Escaped ~ - Reciprocal Relation between the Scaling Exponent and the NSE Characteristic Time at Which the Magnitude of the Deviation from the Diagonal Becomes the Threshold Value u* is Given by ~ -1/ (open circles) =1/ (crosses) 16

Parametric Noise Effect on the Weak Synchronization : Noise Strength (i) (i=1, 2): uniform random variable with and Noise Sensitivity Exponents • Parametric Noise R N-k ( x *k ) [ fa(x, a)(=-x 2): Bounded Chaotic Variable, : Bounded Random Variable] • Additive Noise R N-k ( x *k ) NSEs for Both Cases of the Additive and Parametric Noise Become the Same. 17

Noise Effect on Weak Synchronization for the Mutually-Coupled Case =0: Symmetric Coupling, 0< 1: Asymmetric Coupling Characterization of the Noise Sensitivity R N-k ( x *k ) (2 - )c • By a Scale Change c c/(2 - ), the Result for the NSE in the Unidirectionally Coupled Case ( =1) may be Converted into that for the Mutually Coupled Case (0 <1). [In the Same Way, the PSE for the Mutually Coupled Case can also be Obtained. ] 18

Summary The NSE (PSE) Measures the Degree of the Sensitivity of the SCA with respect to the Noise (Parameter Mismatching); N ~ N (cf. The Transverse Lyapunov Exponent Measures the Degree of the Sensitivity to the Initial Orbit Points. ) Weak Synchronization Strong Synchronization Weak Synchronization < 0 >0 < 0 =0 < 0 >0 First Transverse Bif. • Noise Effect = Parameter-Mismatching Effect ( First Transverse Bif. Blow-out Bif. c Blow-out Bif. NSE=PSE) Characterization of the Bubbling Attractor and Chaotic Transient Power-Law Scaling of the Average Laminar Length and Average Lifetime: ~ - ( - ) • Reciprocal Relation between the Scaling Exponent and the NSE (PSE) =1/ 19

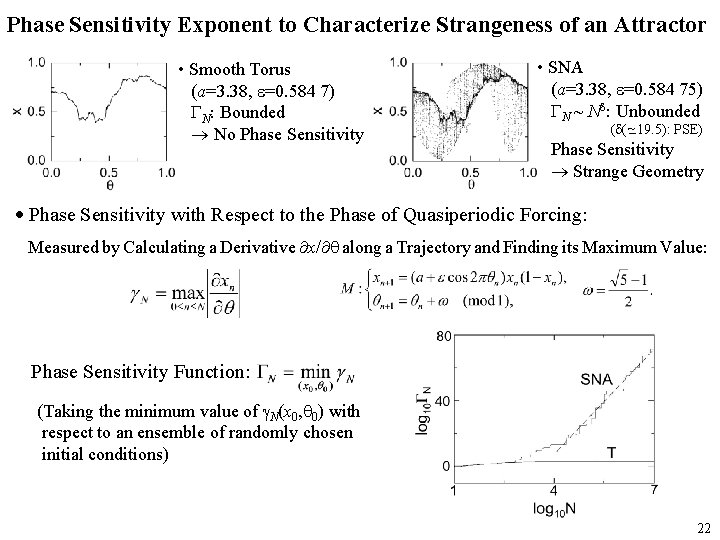
Analogy between the Characteristic Quantities of the Weakly Stable SCA and the Strange Nonchaotic Attractor (SNA) Common Property: A Typical Trajectory on Both the Weakly Stable SCA and the SNA may Have Segments of Arbitrarily Long Length M with Positive Local (M-Time) Lyapunov Exponents Quasiperiodically Forced System The Phase Sensitivity Exponent Measures the Degree of Strangeness of the SNA. Smooth Torus SNA No Phase Sensitivity Chaos Synchronization The Noise (Parameter) Sensitivity Exponent Measures the Degree of the Noise (Parameter) Sensitivity of the Weakly Stable SCA. Strong Synchronization Weak Synchronization No Noise (Parameter) Sensitivity 20

Quasiperiodically Forced Systems : Irrational No. 21

Phase Sensitivity Exponent to Characterize Strangeness of an Attractor • Smooth Torus (a=3. 38, =0. 584 7) N: Bounded No Phase Sensitivity • SNA (a=3. 38, =0. 584 75) N ~ N : Unbounded ( ( ~_ 19. 5): PSE) Phase Sensitivity Strange Geometry Phase Sensitivity with Respect to the Phase of Quasiperiodic Forcing: Measured by Calculating a Derivative x/ along a Trajectory and Finding its Maximum Value: Phase Sensitivity Function: (Taking the minimum value of N(x 0, 0) with respect to an ensemble of randomly chosen initial conditions) 22

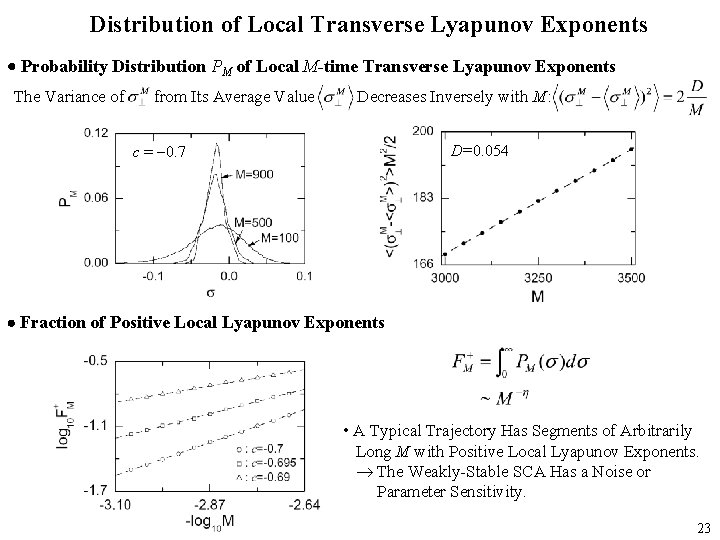
Distribution of Local Transverse Lyapunov Exponents Probability Distribution PM of Local M-time Transverse Lyapunov Exponents The Variance of from Its Average Value Decreases Inversely with M: c = -0. 7 D=0. 054 Fraction of Positive Local Lyapunov Exponents • A Typical Trajectory Has Segments of Arbitrarily Long M with Positive Local Lyapunov Exponents. The Weakly-Stable SCA Has a Noise or Parameter Sensitivity. 23
 Orderly (50%)chaotic (50%)
Orderly (50%)chaotic (50%) Rarran chaotic
Rarran chaotic Low g oscillators 50low
Low g oscillators 50low Sinusoidal oscillators are
Sinusoidal oscillators are Digitally controlled oscillators
Digitally controlled oscillators The figure shows four oscillators at t=0
The figure shows four oscillators at t=0 What is an audio oscillator
What is an audio oscillator Classification of oscillators
Classification of oscillators Types of coupling in multistage amplifier
Types of coupling in multistage amplifier Coupled transport example
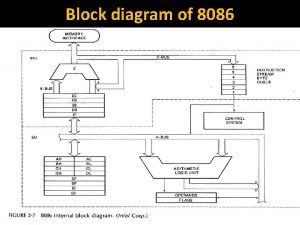
Coupled transport example Block diagram of 8086
Block diagram of 8086 Ecl emitter coupled logic
Ecl emitter coupled logic Charge coupled device
Charge coupled device Frequency response of rc coupled amplifier
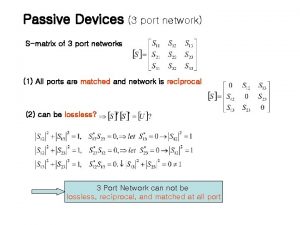
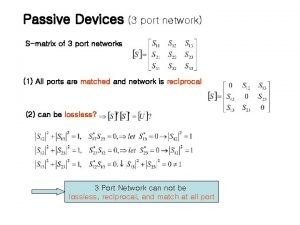
Frequency response of rc coupled amplifier 3 port network
3 port network Magnetically coupled circuits lecture notes
Magnetically coupled circuits lecture notes G=rt ln(q/k)
G=rt ln(q/k) Highly aligned loosely coupled meaning
Highly aligned loosely coupled meaning Magnetically coupled coils
Magnetically coupled coils Coupled model intercomparison project phase 5
Coupled model intercomparison project phase 5 Coupled oscillations
Coupled oscillations Coupled line coupler
Coupled line coupler Charge coupled device detector
Charge coupled device detector Claim of value examples sentence
Claim of value examples sentence