Synchronization in large networks of coupled phase oscillators

Synchronization in large networks of coupled phase oscillators: The effect of network topology Edward Ott University of Maryland 1

Examples of Synchronized Oscillators • Cellular clocks in the brain. • Pacemaker cells in the heart. • Pedestrians on a bridge. • Electric circuits. • Laser arrays. • Oscillating chemical reactions. • Bubbly fluids. • Neutrino oscillations. • Parkinson’s disease. 2

Male fireflies flashing in unison 3

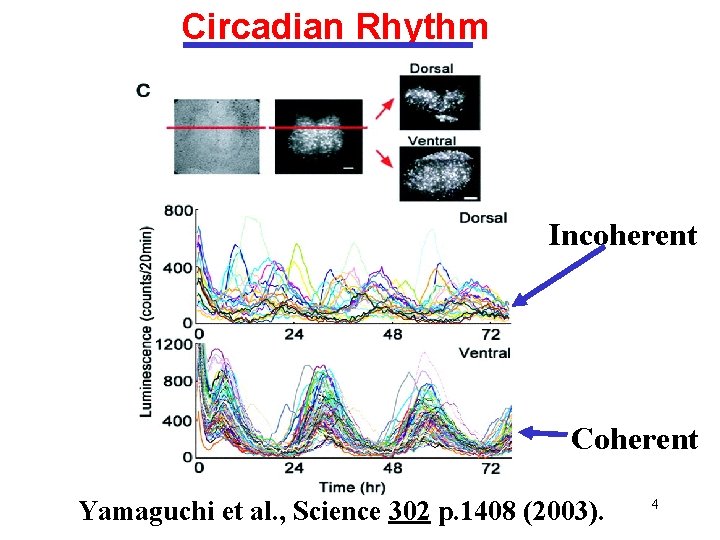
Circadian Rhythm Incoherent Coherent Yamaguchi et al. , Science 302 p. 1408 (2003). 4

Synchrony in the Brain 5

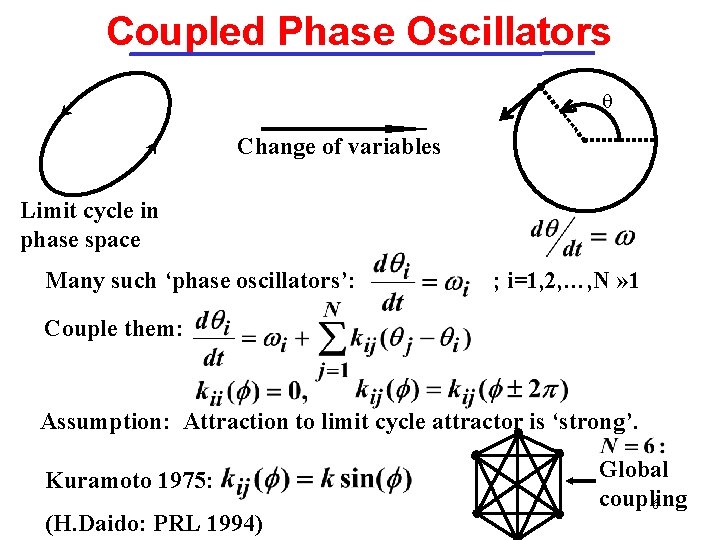
Coupled Phase Oscillators q Change of variables Limit cycle in phase space Many such ‘phase oscillators’: ; i=1, 2, …, N » 1 Couple them: Assumption: Attraction to limit cycle attractor is ‘strong’. Kuramoto 1975: (H. Daido: PRL 1994) Global coupling 6

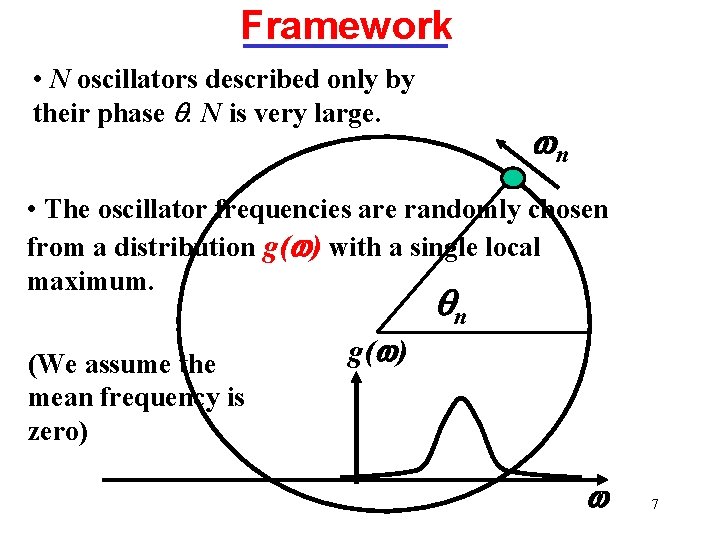
Framework • N oscillators described only by their phase q. N is very large. n • The oscillator frequencies are randomly chosen from a distribution g( ) with a single local maximum. (We assume the mean frequency is zero) g( ) qn 7

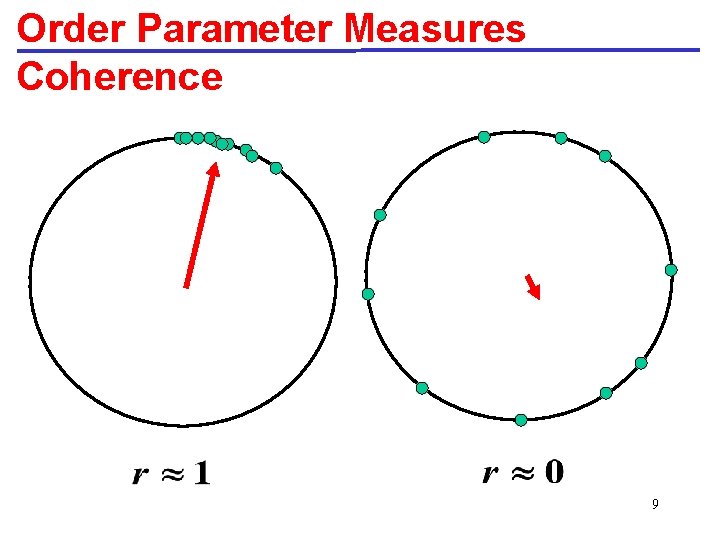
Kuramoto Model: All-to-All Coupling n = 1, 2, …. , N k = (coupling constant) • Assumes sinusoidal all-to-all coupling. • Macroscopic coherence of the system is characterized by = “order parameter” 8

Order Parameter Measures Coherence 9

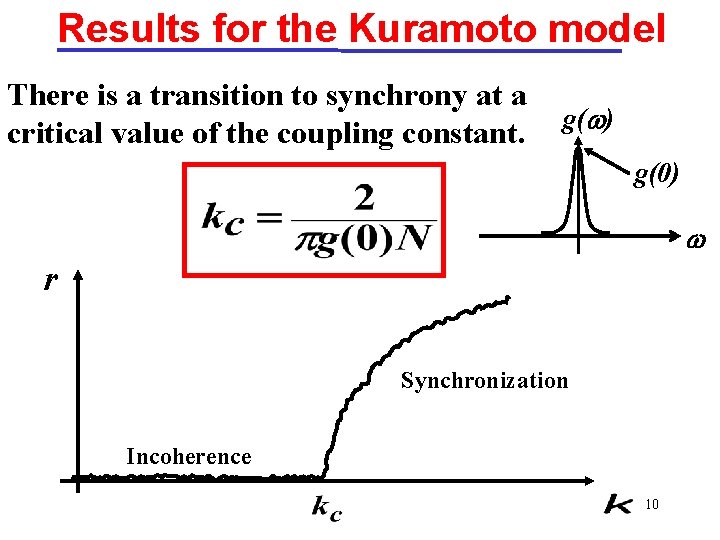
Results for the Kuramoto model There is a transition to synchrony at a critical value of the coupling constant. g( ) g(0) r Synchronization Incoherence 10

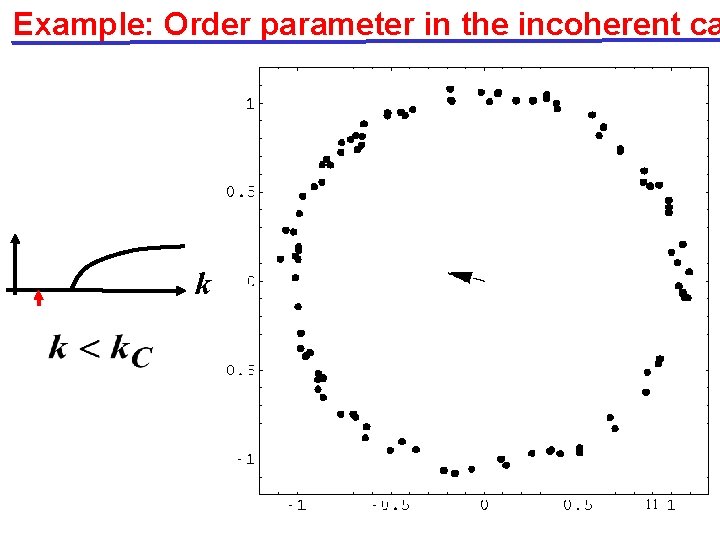
Example: Order parameter in the incoherent ca k 11

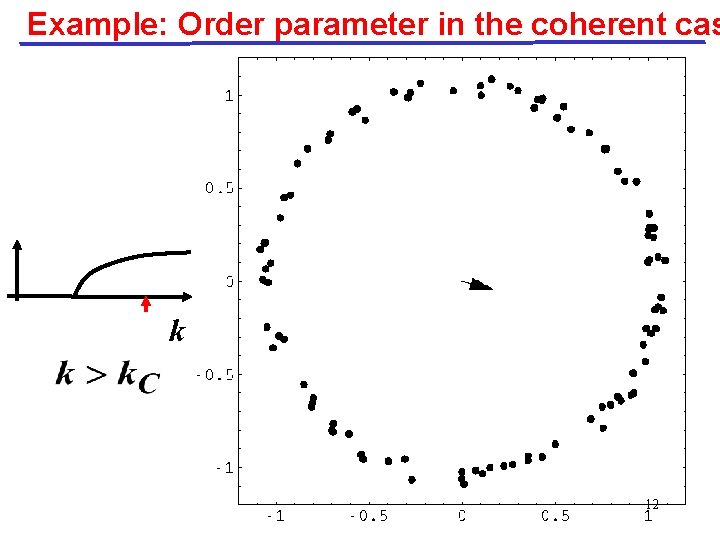
Example: Order parameter in the coherent cas k 12

Derivation of kc “The order parameter” 13

N→∞ Introduce the distribution function F(q, , t) [the fraction of oscillators with phases in the range (q, q+dq ) and freqs. in the range ( , +d ) ] Conservation of number of oscillators: 0 14

Incoherent solution (uniform distribution in angle) 0 Q. A. 0 Is it stable? Yes, for k<kc. No, for k > kc. Stability analysis perturbation 15

Dispersion relation Look for a solution of the form Get 16

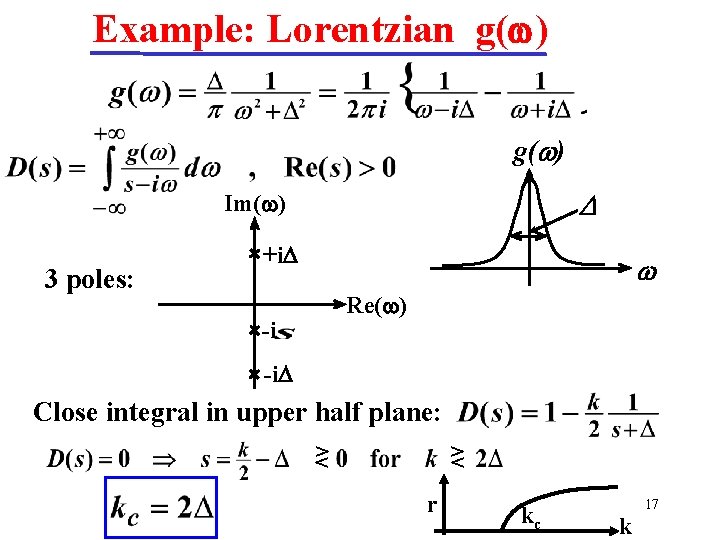
Example: Lorentzian g(w) g( ) D Im(w) 3 poles: +i. D Re(w) -i -i. D Close integral in upper half plane: > < r kc 17 k

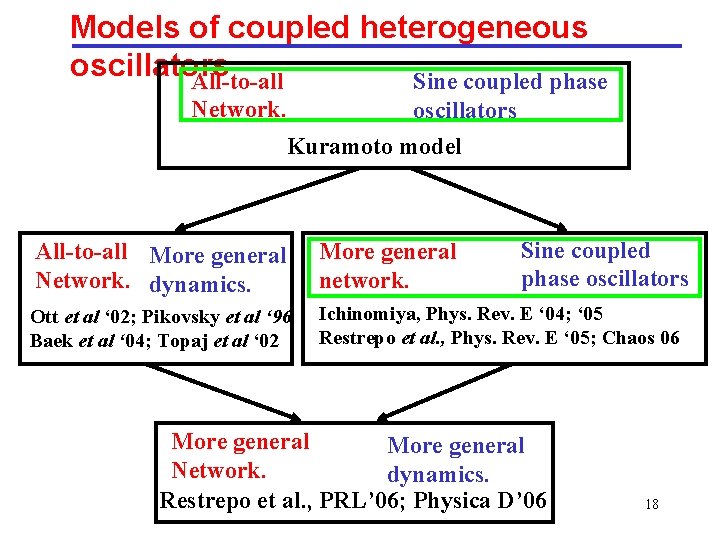
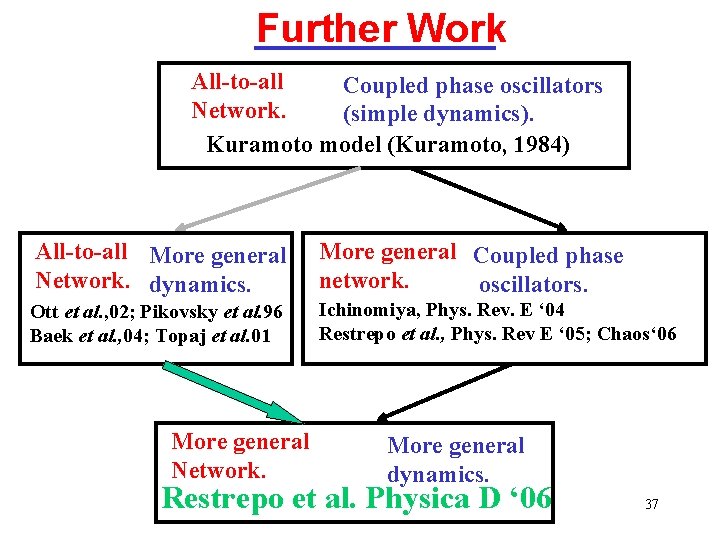
Models of coupled heterogeneous oscillators All-to-all Sine coupled phase Network. oscillators Kuramoto model Sine coupled phase oscillators All-to-all More general Network. dynamics. More general network. Ott et al ‘ 02; Pikovsky et al ‘ 96 Baek et al ‘ 04; Topaj et al ‘ 02 Ichinomiya, Phys. Rev. E ‘ 04; ‘ 05 Restrepo et al. , Phys. Rev. E ‘ 05; Chaos 06 More general Network. dynamics. Restrepo et al. , PRL’ 06; Physica D’ 06 18

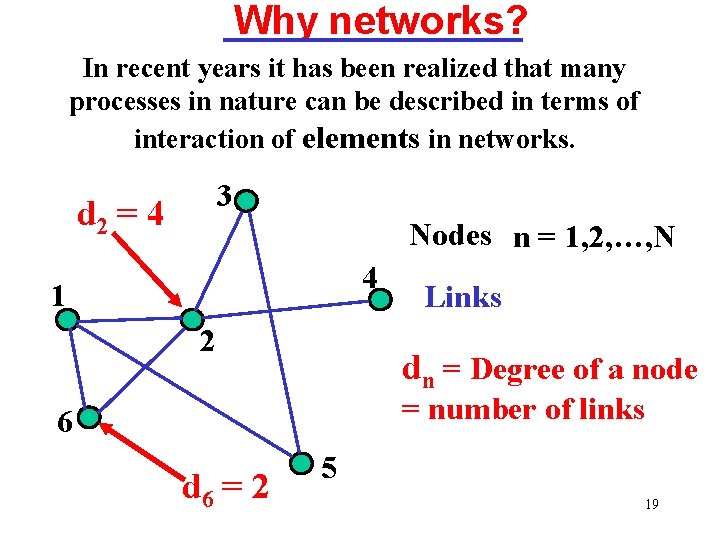
Why networks? In recent years it has been realized that many processes in nature can be described in terms of interaction of elements in networks. 3 d 2 = 4 Nodes n = 1, 2, …, N 4 1 2 Links dn = Degree of a node = number of links 6 d 6 = 2 5 19

Real world networks are often complex 20 http: //www. caida. org/Papers/Nae/ Map of the Internet

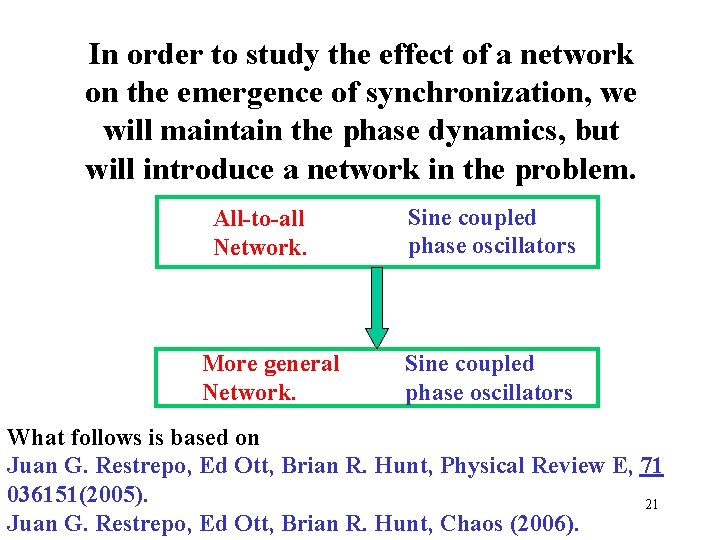
In order to study the effect of a network on the emergence of synchronization, we will maintain the phase dynamics, but will introduce a network in the problem. All-to-all Network. More general Network. Sine coupled phase oscillators What follows is based on Juan G. Restrepo, Ed Ott, Brian R. Hunt, Physical Review E, 71 036151(2005). 21 Juan G. Restrepo, Ed Ott, Brian R. Hunt, Chaos (2006).

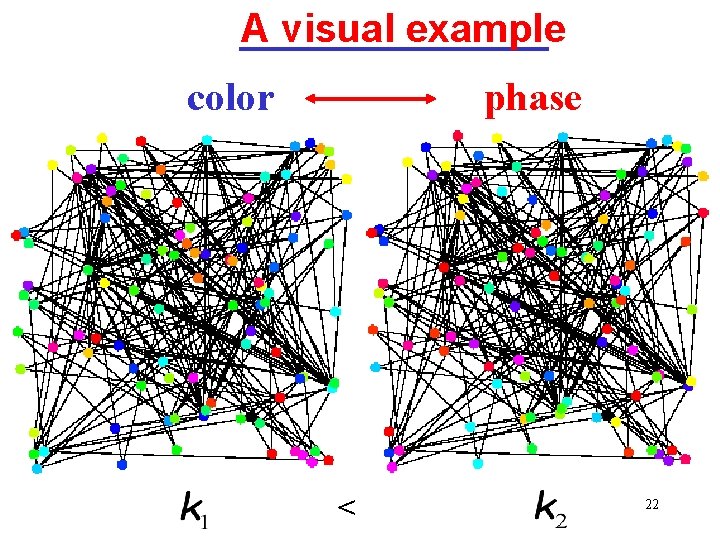
A visual example color phase < 22

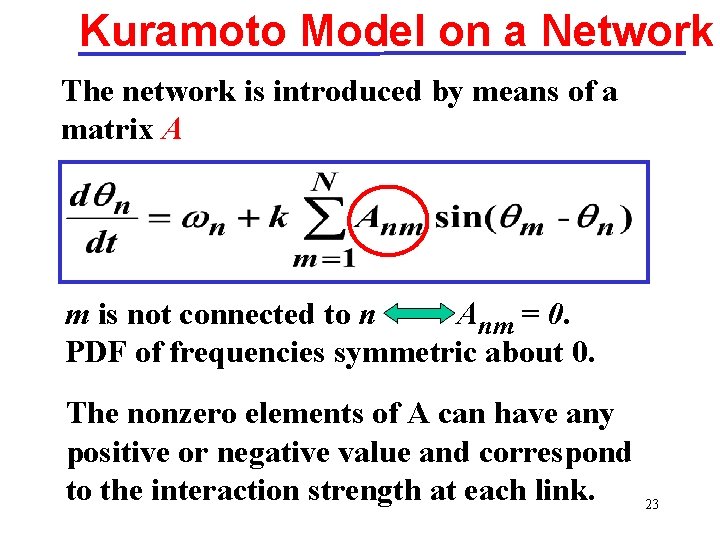
Kuramoto Model on a Network The network is introduced by means of a matrix A m is not connected to n Anm = 0. PDF of frequencies symmetric about 0. The nonzero elements of A can have any positive or negative value and correspond to the interaction strength at each link. 23

Order Parameter Description Local order parameter for node n where = time average. Global order parameter: where is the node degree: PROBLEM: Find r vrs. k 24

Order Parameter Form of the Dynamics and yield where. 25

Neglect of hn Assumption: The degree is large. There are many terms in the determining is noise-like. Neglect hn compared to O(dn) The effect of finite hn is treated in Restrepo, Ott and Hunt Phys. Rev. E (2005), Sec 26 6. .

Time Averaged Approximation ; Locked nodes: Putting this in the equation for using and , gives the time averaged approximation. (Restrepo, Ott, Hunt, PRE 2005) , 27

Frequency Distribution Approximation Assuming rn is independent of n we can average over the frequencies to get 0 Knowledge of each individual frequency is not needed. g( ) g(0) The onset of synchronization corresponds to rn 0+. We obtain an eigenvalue equation! 28

Mean Field Approximation Assuming rn = r dn , we get the mean field approximation ( Ichinomiya, 2004 ): Near the transition, it has the extra assumption that the eigenvector u of A with the largest eigenvalue satisfies un dn. Only knowledge of the degree and frequency 29 distributions is required.

Results g( ) • For a large class of networks, there is still a transition tog(0) synchrony at a critical coupling strength k. C. • We have developed several approximations to the order parameter past the transition. • The critical coupling strength is given by Network All-to-all: Kuramoto model is the largest eigenvalue of the matrix A defining the network. 30

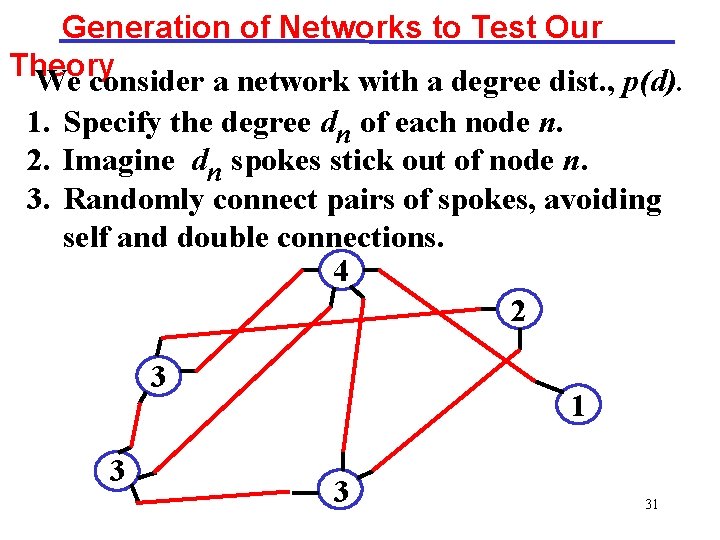
Generation of Networks to Test Our Theory We consider a network with a degree dist. , p(d). 1. Specify the degree dn of each node n. 2. Imagine dn spokes stick out of node n. 3. Randomly connect pairs of spokes, avoiding self and double connections. 4 2 3 3 1 3 31

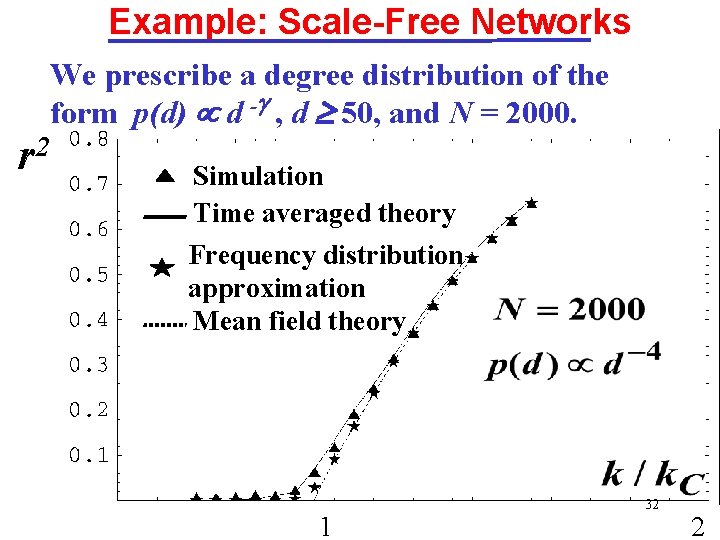
Example: Scale-Free Networks 2 r We prescribe a degree distribution of the form p(d) d - , d 50, and N = 2000. Simulation Time averaged theory Frequency distribution approximation Mean field theory 1 32 2

Example: Scale-Free Networks r 2 Simulation Time averaged theory Frequency distribution approximation Mean field theory 1 33 2

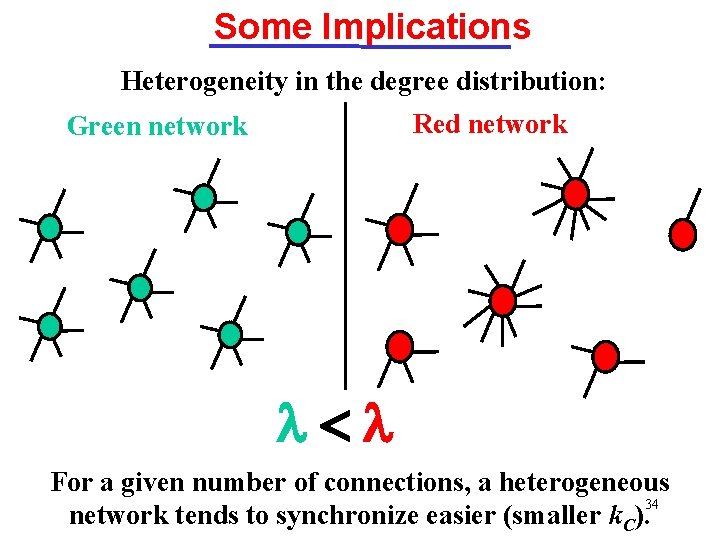
Some Implications Heterogeneity in the degree distribution: Red network Green network l<l For a given number of connections, a heterogeneous 34 network tends to synchronize easier (smaller k. C).

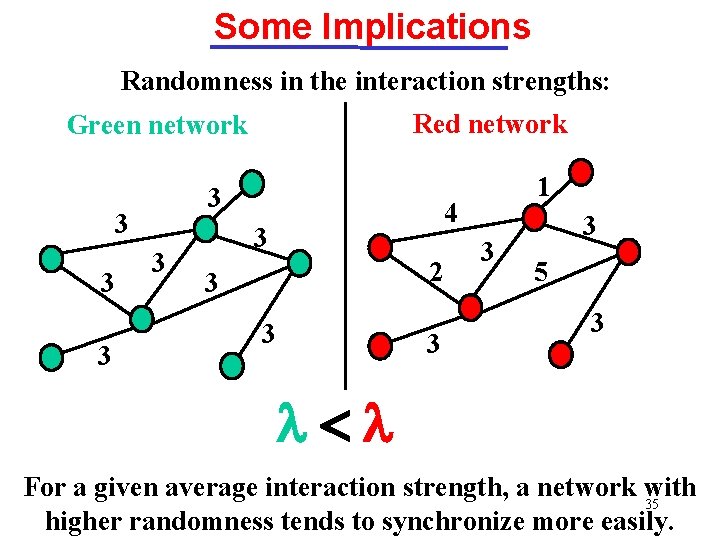
Some Implications Randomness in the interaction strengths: Red network Green network 3 3 3 1 4 3 2 3 3 3 5 3 l<l For a given average interaction strength, a network with 35 higher randomness tends to synchronize more easily.

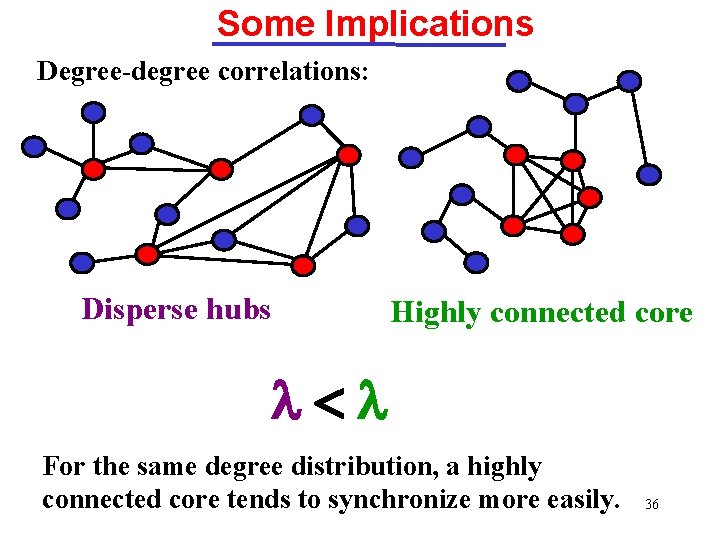
Some Implications Degree-degree correlations: Disperse hubs Highly connected core l<l For the same degree distribution, a highly connected core tends to synchronize more easily. 36

Further Work All-to-all Coupled phase oscillators Network. (simple dynamics). Kuramoto model (Kuramoto, 1984) All-to-all More general Network. dynamics. More general Coupled phase network. oscillators. Ott et al. , 02; Pikovsky et al. 96 Baek et al. , 04; Topaj et al. 01 Ichinomiya, Phys. Rev. E ‘ 04 Restrepo et al. , Phys. Rev E ‘ 05; Chaos‘ 06 More general Network. More general dynamics. Restrepo et al. Physica D ‘ 06 37

Networks with General Node Dynamics Uncoupled node dynamics: Could be periodic or chaotic. Kuramoto is a special case: Main result: Q: depends on the collection of node dynamical behaviors (not on network topology). l: Max. eigenvalue of A; depends on network topology (not on node dynamics). Restrepo, Hunt, Ott, PRL ‘ 06; Physica D ‘ 06 38

39

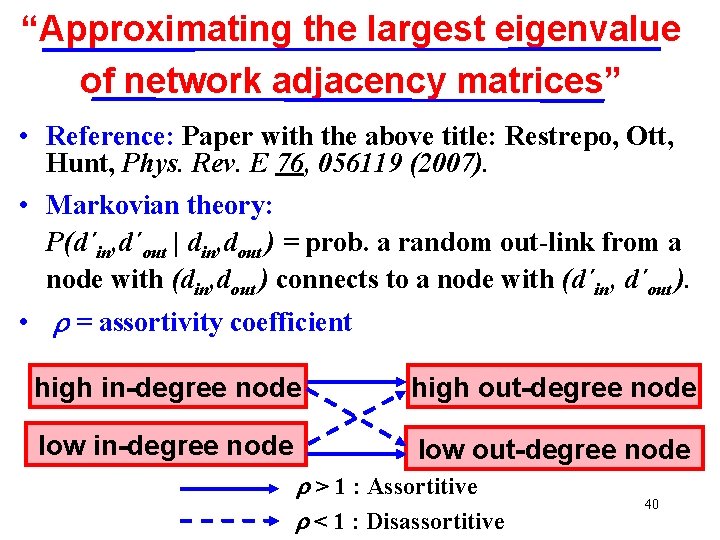
“Approximating the largest eigenvalue of network adjacency matrices” • Reference: Paper with the above title: Restrepo, Ott, Hunt, Phys. Rev. E 76, 056119 (2007). • Markovian theory: P(d´in, d´out | din, dout ) = prob. a random out-link from a node with (din, dout ) connects to a node with (d´in, d´out ). • = assortivity coefficient high in-degree node high out-degree node low in-degree node low out-degree node > 1 : Assortitive < 1 : Disassortitive 40

Test of Markovian theory Randomly generated A’s with N=25, 000, <d> = 20. P(d) d-2. 5 Dashed line: expansion about ρ=1. Solid black line: actual eigenvalue. Squares: Markovian approximation. P(din, dout ) (dindout )-2. 5 41

Summary • For a large class of networks, there is a transition to synchrony at a critical coupling constant determined by the maximum eigenvalue of the adjacency matrix. • A larger maximum eigenvalue of the adjacency matrix favors a lower threshold for synchronization. • Heterogeneity in the degree distribution, randomness in the couplings, and positive degree correlations favors synchronization. Our papers can be obtained from: http: //www. chaos. umd. edu/umdsyncnets. html 42

What is the effect of complex interaction structure on dynamical processes taking place in networks? We will focus on the synchronization of coupled heterogeneous oscillators. 43

Effect of the nodes with small degree So far we have been using the average value of rn. However, Finite degree dn Fluctuations What is the effect of the fluctuations? 44

Perturbations from the incoherent state The incoherent state is given by We introduce perturbations and assume . Onset of synchronization 45

Time fluctuations as noise The original equations are If the degree dn is large but finite and the system is incoherent, the coupling term can be approximated by a Gaussian random noise with diffusion coefficient Dn. Smaller degree dn Larger diffusion coefficient Dn 46

Theoretical results We obtain the eigenvalue equation If Dn = 0, letting we get Positive Dn corresponds to a smaller growth rate and thus to a larger critical coupling strength. 47

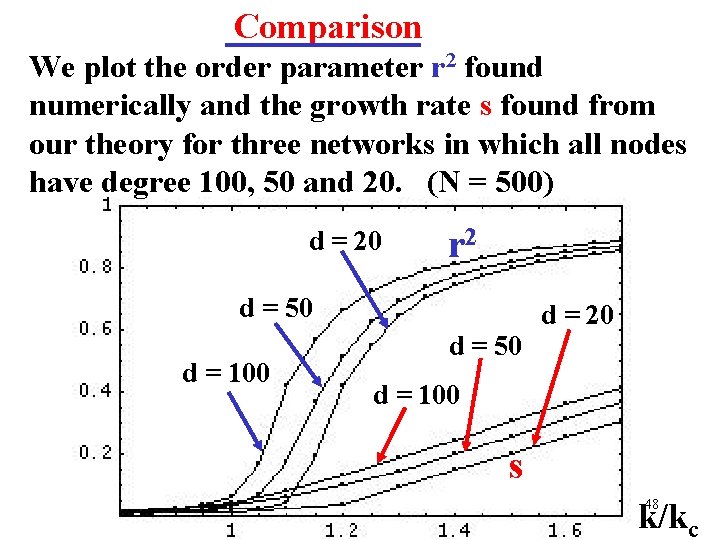
Comparison We plot the order parameter r 2 found numerically and the growth rate s found from our theory for three networks in which all nodes have degree 100, 50 and 20. (N = 500) d = 20 r 2 d = 50 d = 100 d = 20 d = 50 d = 100 s k/kc 48

AN EXAMPLE 5000 Lorenz systems: Network: N=5000; References: Restrepo, Ott, Hunt, Physica D (2006) 49 [Ott, So, Barreto, Antonsen, Physica D(2002)]