Surface Reconstruction From Unorganized Point Sets piyushcs Example

Surface Reconstruction From Unorganized Point Sets piyush@cs

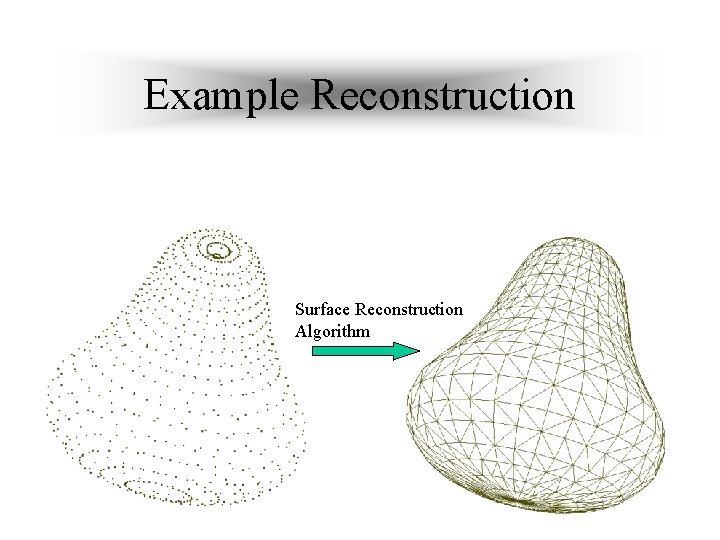
Example Reconstruction Surface Reconstruction Algorithm

Organization of Talk • • Problem Statement Some Basic Definitions Hoppe’s Algorithm : The Beginning Alpha Shapes : Generalizations of the convex hull Crust : A Narrow problem specification New Algorithms on the Horizon Open Problems

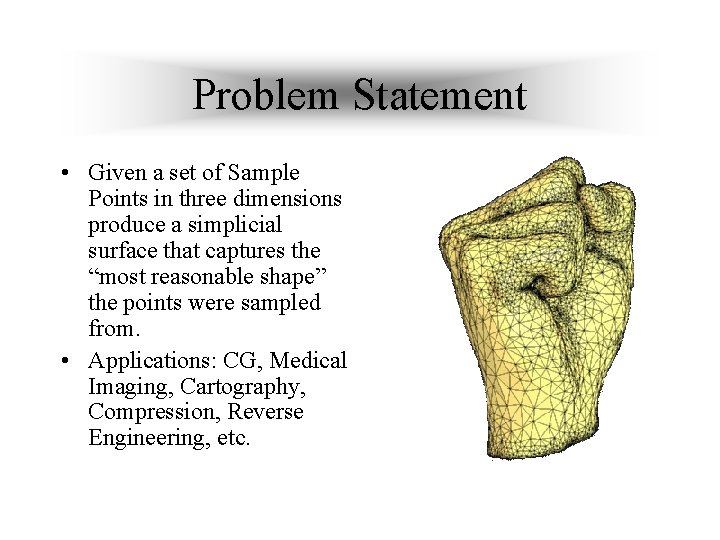
Problem Statement • Given a set of Sample Points in three dimensions produce a simplicial surface that captures the “most reasonable shape” the points were sampled from. • Applications: CG, Medical Imaging, Cartography, Compression, Reverse Engineering, etc.

Definitions Delaunay Triangulation, Voronoi Diagram[2 D, 3 D]

Hoppe et al’s Algorithm Ø Estimate Signed Distance Function -ve Ø Use Iso-Surface Extraction after this step +ve

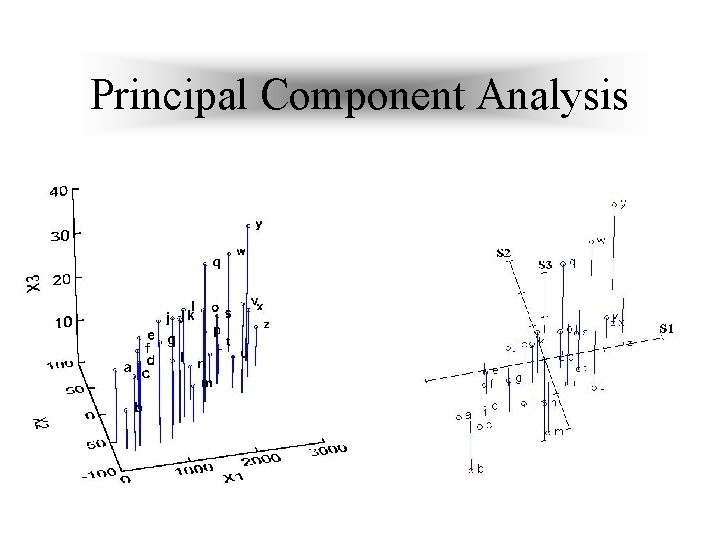
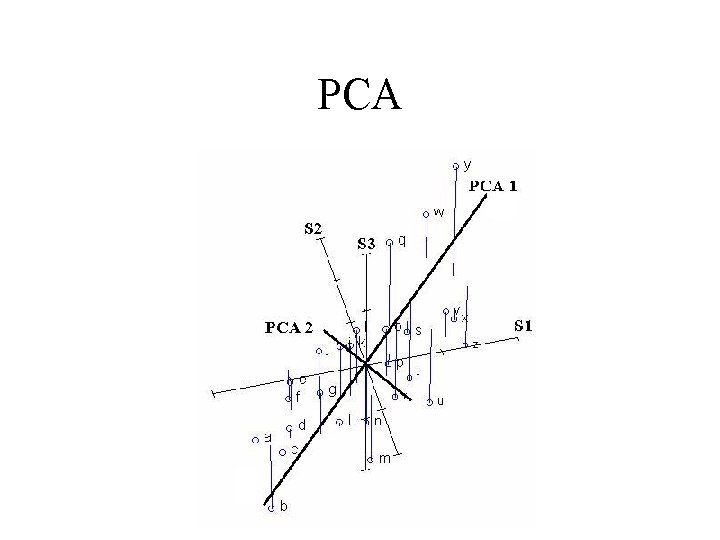
Hoppe et al’s Algorithm Ø Tangent Plane Estimation(PCA) Ø Consistent tangent plane orientation(MST) Ø Signed distance function Ø Contour tracing (Marching Cubes)

Principal Component Analysis

PCA

Sample Output

Problems with Hoppe’s Algorithm • All k-nearest neighbors might lie on a single line in some cases hence creating a problem for the normal computation. • The Sampling criterion required is uniform. Sampling ideally should be proportional to curvature in some sense. Ø Curless Levoy gave a modification which is one of the best results in Practice.

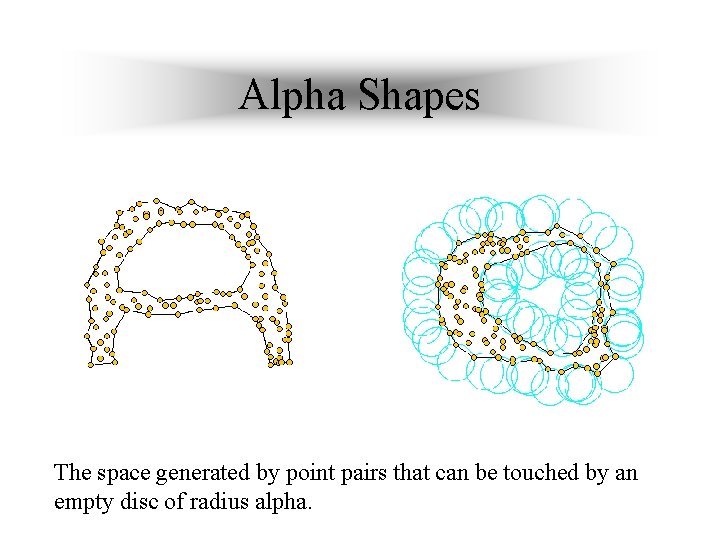
Alpha Shapes The space generated by point pairs that can be touched by an empty disc of radius alpha.

Alpha Shapes Alpha Controls the desired level of detail.

Sample Outputs

Problems with Alpha Shapes • Global Value of Alpha may not exist for a correct reconstruction in some cases • Experimentation is required to find the appropriate values of alpha • A Delaunay computation is done on the point set which is costly in 3 D

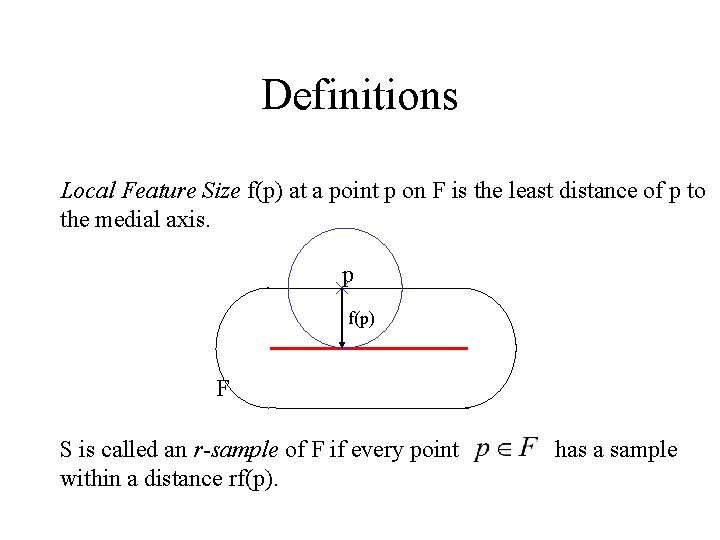
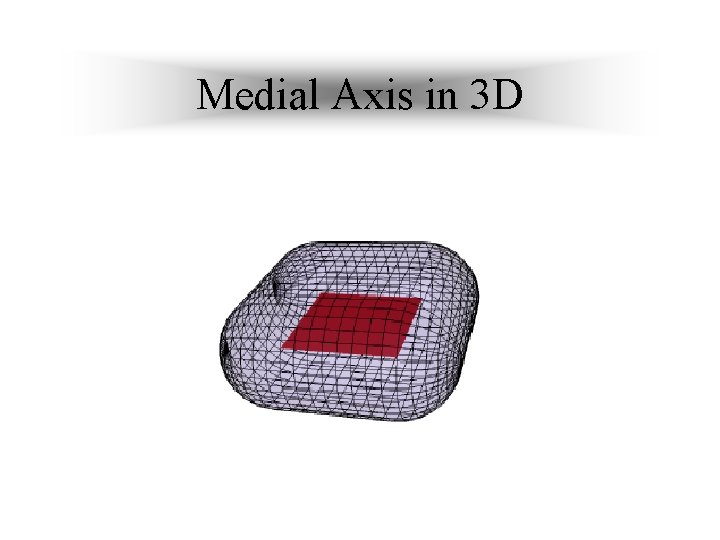
Crust: A Narrow problem Specification ØAims to reconstruct only smooth closed Manifolds in 2 D and 3 D Medial Axis: of surface F is the closure of points that have more than one closest point in F.

Definitions Local Feature Size f(p) at a point p on F is the least distance of p to the medial axis. p f(p) F S is called an r-sample of F if every point within a distance rf(p). has a sample

The Intuition behind Crust The Voronoi Cells of a dense sampling are thin and long. The Medial Axis is the extension of Voronoi Diagram for continuous surfaces in the sense that the Voronoi Diagram of S Can be defined as the set of points with more than one closest point in S. (S = Sample Point Set) The Sampling criterion of the Crust breaks down in case of non-smooth curves and surfaces.

The Crust in 2 D Input : P = Set of sample points in the plane Output: E = Set of edges connecting points in P The Algorithm Compute the Voronoi vertices of P = V Calculate the Delaunay of (P U V) Pick the edges (p, q) where both p, q are in P

Sample Output

3 D Crust: Definitions Restricted Voronoi Cells: Restricted Delaunay Triangles: A triangle is nonempty. Here S is a surface and p is a sample point. (What is a correct connection in 3 D? ? )

Medial Axis in 3 D

The Problem with 3 D • Slivers : Even very dense sampling does not guarantee that the Voronoi Vertices approximate the Medial axis which is true in case of 2 D Crust. Actually the Voronoi Vertices in 3 D can be arbitrarily far from the Medial Axis.

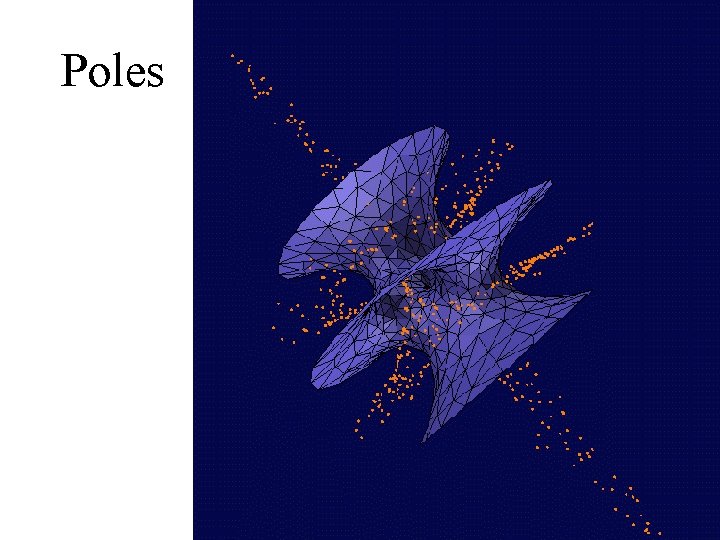
Crust in 3 D • Compute the 3 D Voronoi diagram of the sample points. • For each sample point s, pick the farthest vertex v of its Voronoi cell, and the farthest vertex v' such that angle vsv' exceeds 90 degrees. • Compute the Voronoi diagram of the sample points and the "poles", the Voronoi vertices chosen in the second step. • Add a triangle on each triple of sample points with neighboring cells in the second Voronoi diagram.

Poles

Sample Output

Problems with Crust • • • Very Slow in 3 D for large pointsets Cannot handle Boundaries Cannot deal with Sharp turns and Corners Needs computation of Delaunay Twice Theoretically requires very high density sampling in 3 D (r <=. 06)

The Hot Solutions • Spiralling Edge (P. Crossno & E. Angel, Visualization 99)* • Interactive Approach (L. P. Kobelt and M. Botsch, Euro. Graphics 2 k) • Surface Reconstruction based on Lower Dimensional Localized Delaunay Triangulation (Gopi et al. , Eurographics 2000) • Single Pass Crust(Amenta et al, So. CG 2 k)* • Graph-Based Surface Reconstruction Using Structures in Scattered Point Sets (R. Mencl and H. Müller in CGI 98)*

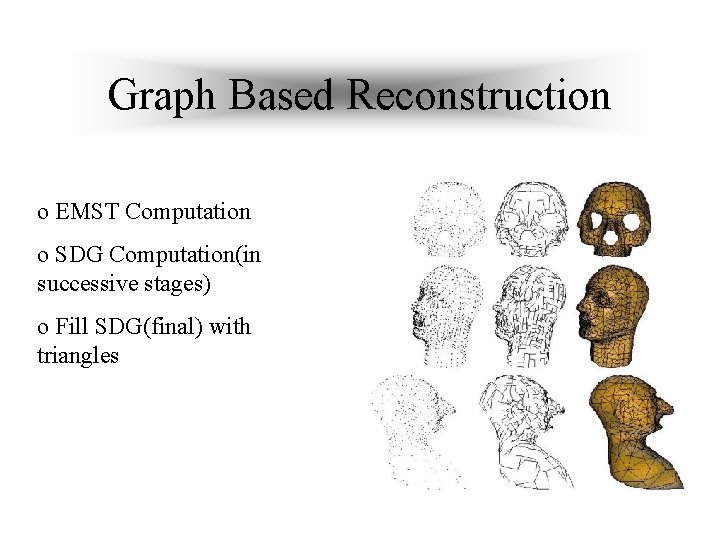
Graph Based Reconstruction o EMST Computation o SDG Computation(in successive stages) o Fill SDG(final) with triangles

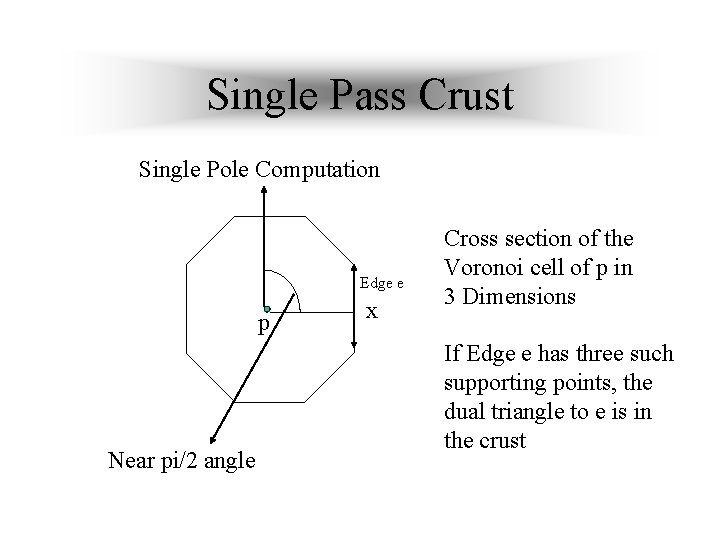
Single Pass Crust Single Pole Computation Edge e p Near pi/2 angle x Cross section of the Voronoi cell of p in 3 Dimensions If Edge e has three such supporting points, the dual triangle to e is in the crust

Spiralling Edge • Advancing Front Flavour: Uses Edge Rings. • Gabriel Graph Computation in k-nearest neighbours. • Starts with normal information. • Handles Boundary and Corner points as special cases. • No Theoretical Guarantees.

Reviver http: //reviver. homepage. com

Reviver

Problems with Reviver

Open Problems • Provable reconstruction for Manifolds with boundary and sharp turns. • Can Provable algorithms be given using subset of Delaunay instead of global Delaunay computation? • Can Unorganised points be decimated before reconstruction?