Example 1 Example 2 Example 3 Example 4

Example 1 Example 2 Example 3 Example 4 Example 5 Solve a Rational Equation Elimination of a Possible Solution Work Problem Rate Problem Solve a Rational Inequality

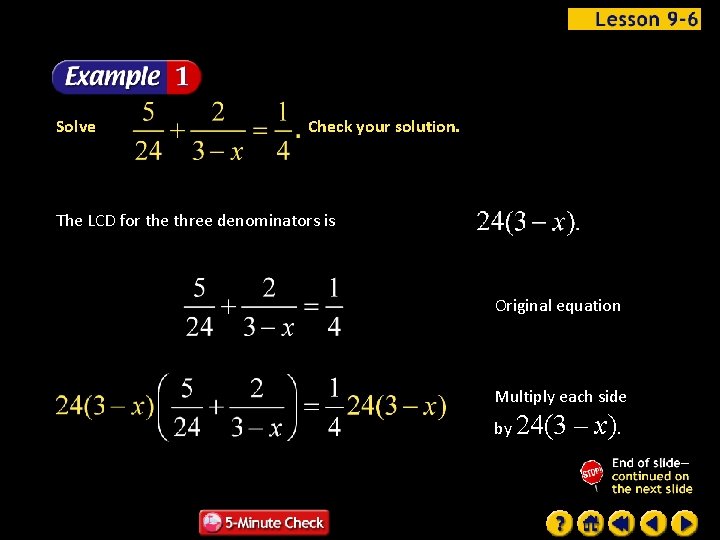
Solve Check your solution. The LCD for the three denominators is Original equation Multiply each side by 24(3 – x).

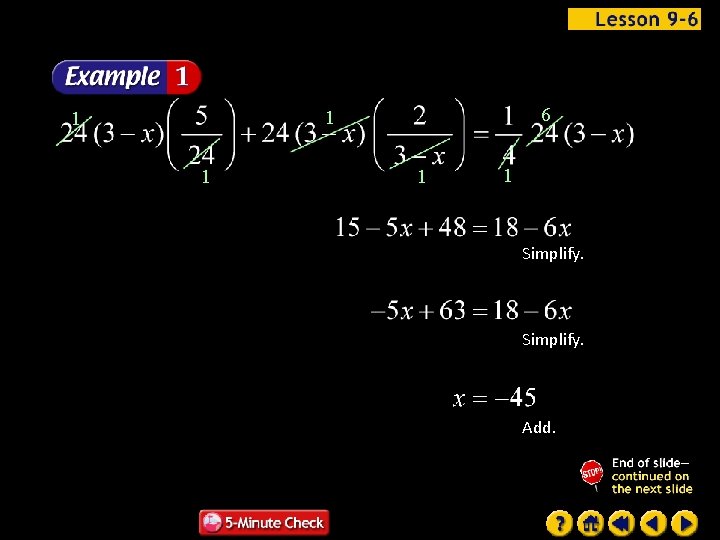
6 1 1 1 Simplify. Add.

Check Original equation Simplify. The solution is correct.

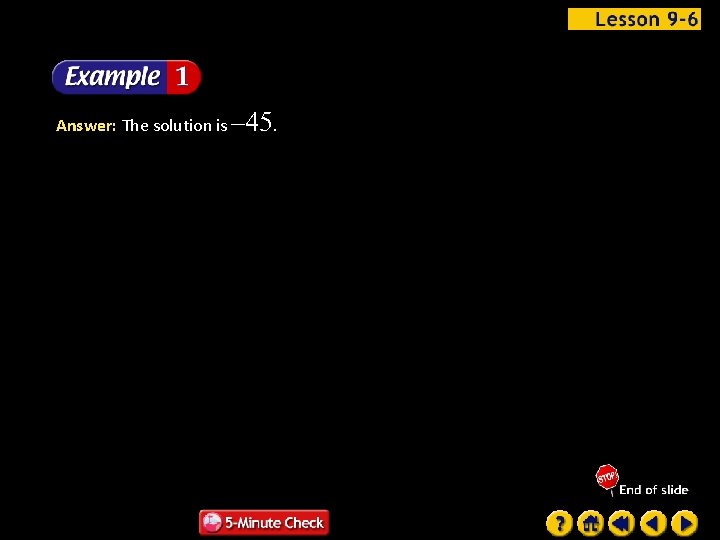
Answer: The solution is – 45.

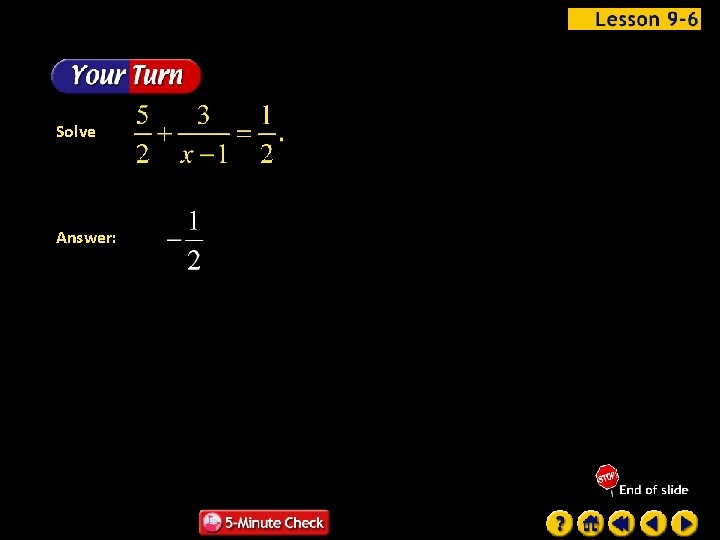
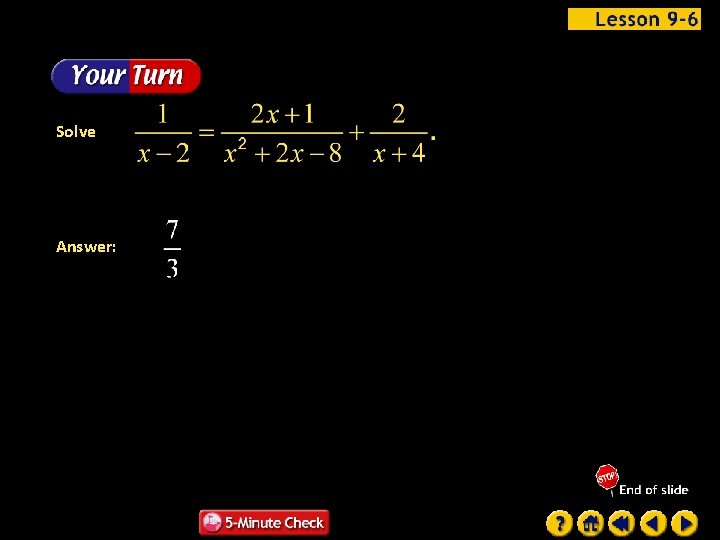
Solve Answer:

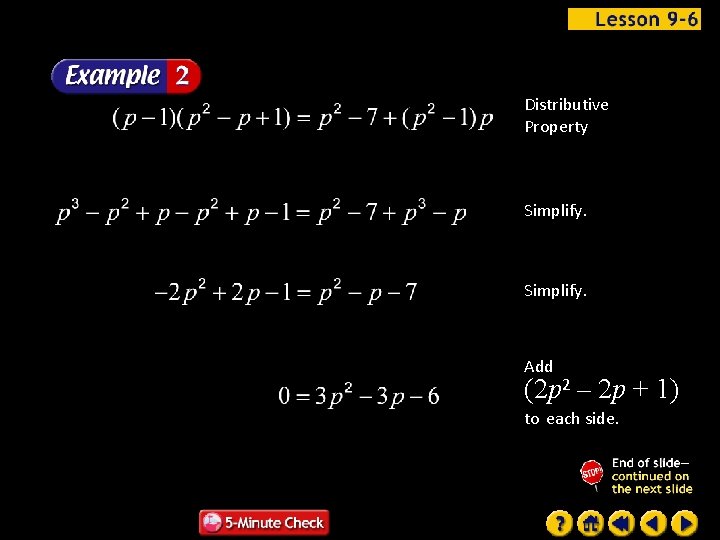
Solve Check your solution. The LCD is Original equation p– 1 1 Multiply by the LCD, (p 2 – 1).

Distributive Property Simplify. Add (2 p 2 – 2 p + 1) to each side.

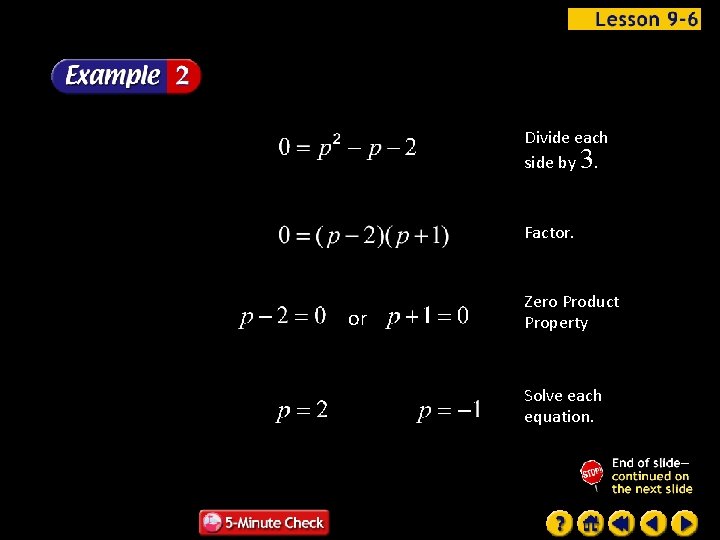
Divide each side by 3. Factor. or Zero Product Property Solve each equation.

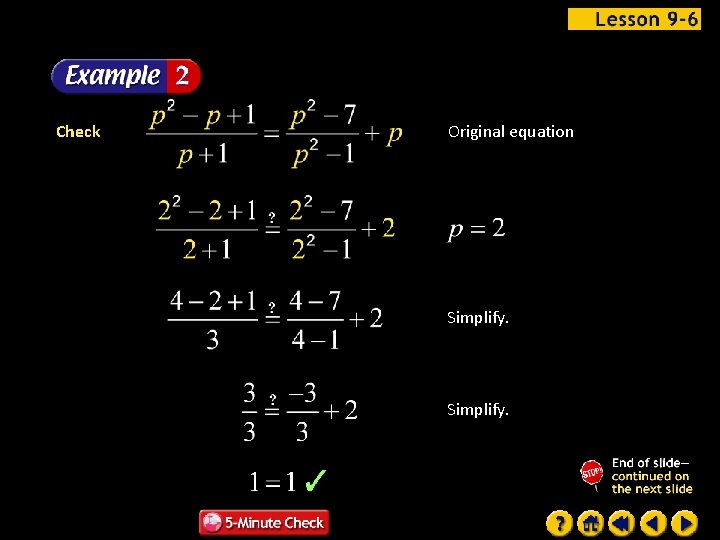
Check Original equation Simplify.

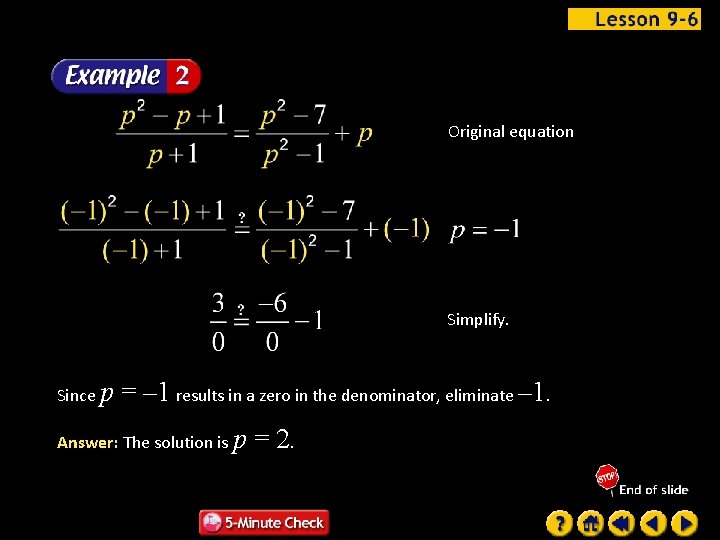
Original equation Simplify. Since p = – 1 results in a zero in the denominator, eliminate – 1. Answer: The solution is p = 2.

Solve Answer:

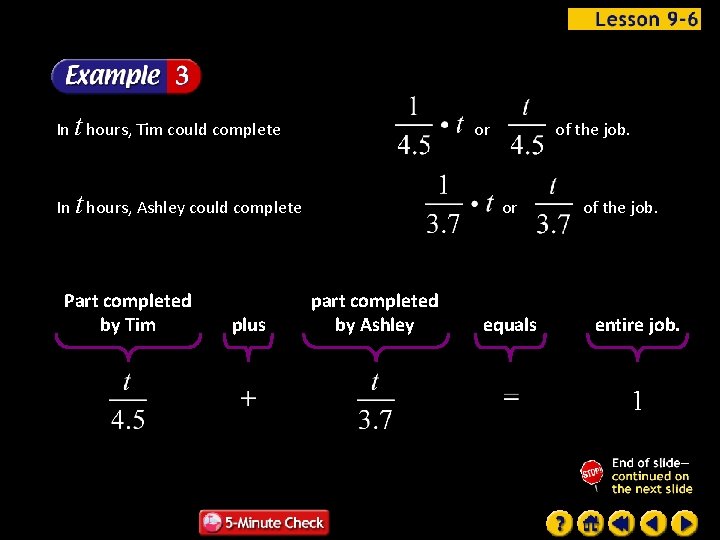
Mowing Lawns Tim and Ashley mow lawns together. Tim working alone could complete the job in 4. 5 hours, and Ashley could complete it alone in 3. 7 hours. How long does it take to complete the job when they work together? In 1 hour, Tim could complete In 1 hour, Ashley could complete of the job.

In t hours, Tim could complete or In t hours, Ashley could complete Part completed by Tim plus of the job. or part completed by Ashley equals of the job. entire job. 1

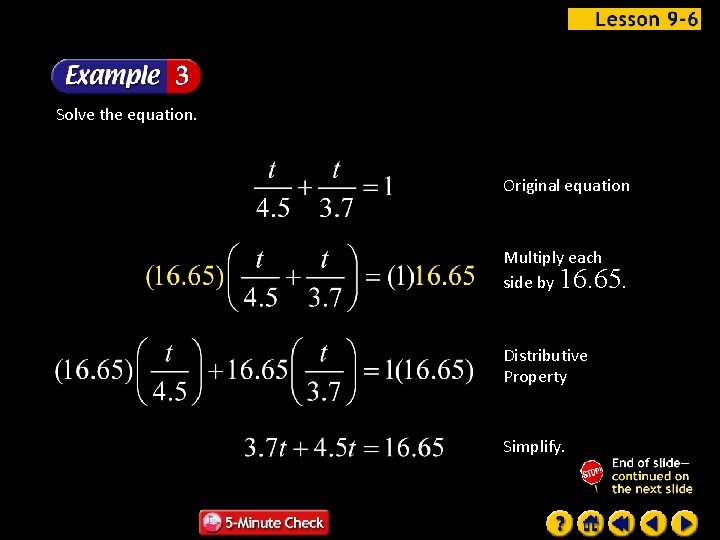
Solve the equation. Original equation Multiply each side by 16. 65. Distributive Property Simplify.

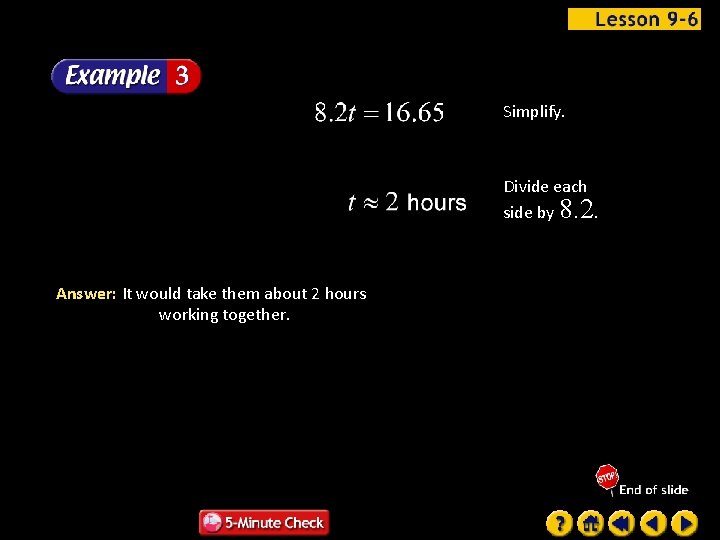
Simplify. Divide each side by 8. 2. Answer: It would take them about 2 hours working together.

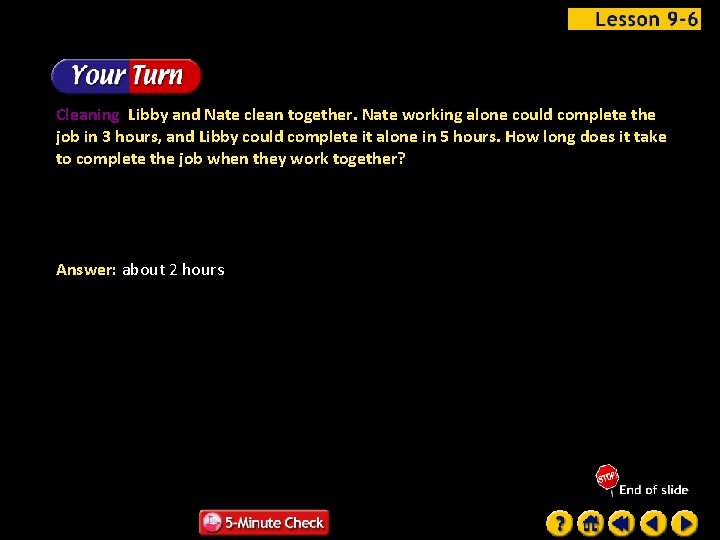
Cleaning Libby and Nate clean together. Nate working alone could complete the job in 3 hours, and Libby could complete it alone in 5 hours. How long does it take to complete the job when they work together? Answer: about 2 hours

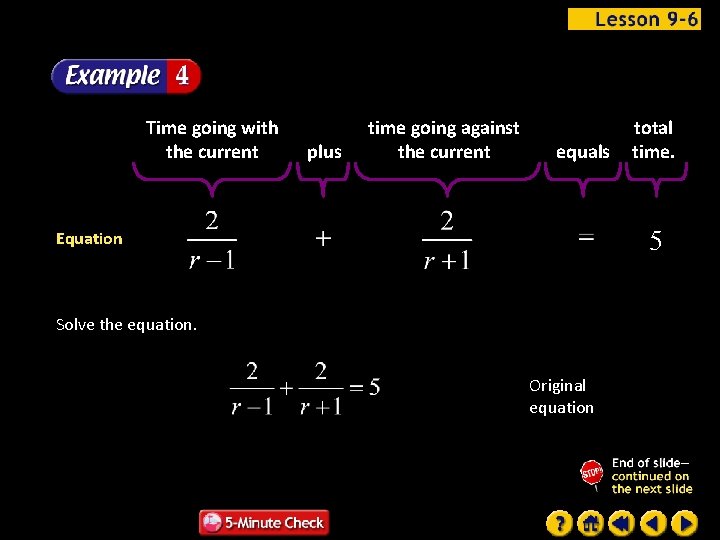
Swimming Janine swims for 5 hours in a stream that has a current of 1 mile per hour. She leaves her dock and swims upstream for 2 miles and then back to her dock. What is her swimming speed in still water? Words The formula that relates distance, time, and rate is Variables Let r be her speed in still water. Then her speed with the current is r + 1 and her speed against the current is r – 1.

Time going with the current plus time going against the current equals total time. 5 Equation Solve the equation. Original equation

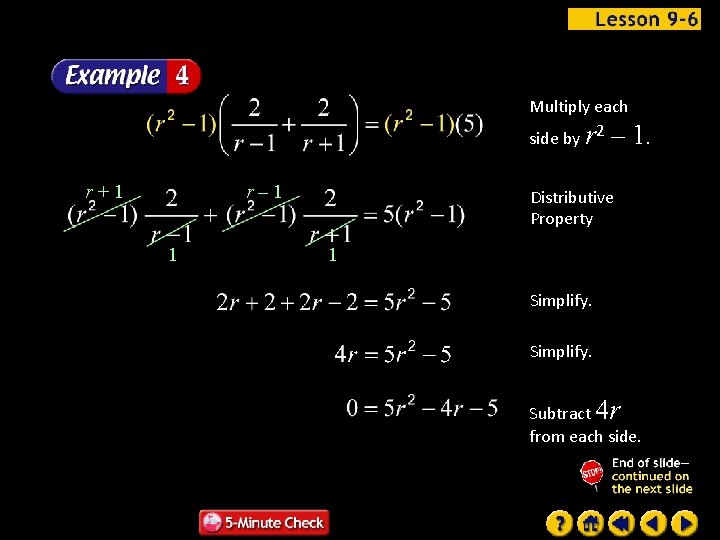
Multiply each side by r 2 – 1. r+1 r– 1 1 Distributive Property 1 Simplify. Subtract 4 r from each side.

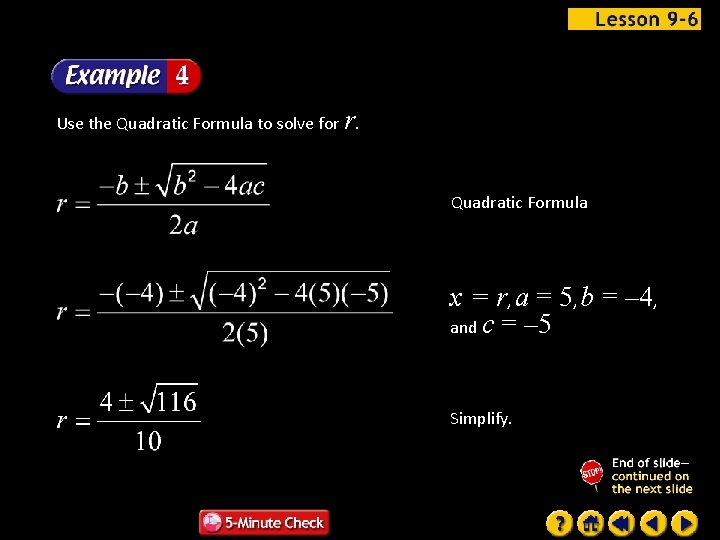
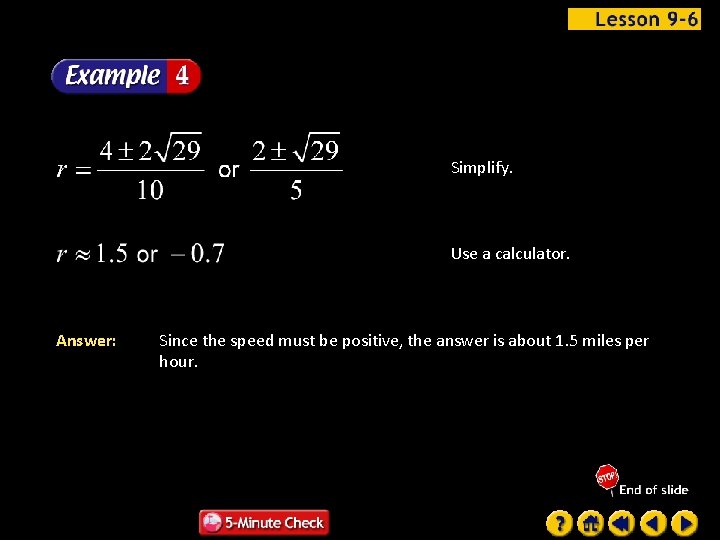
Use the Quadratic Formula to solve for r. Quadratic Formula x = r, a = 5, b = – 4, and c = – 5 Simplify.

Simplify. Use a calculator. Answer: Since the speed must be positive, the answer is about 1. 5 miles per hour.

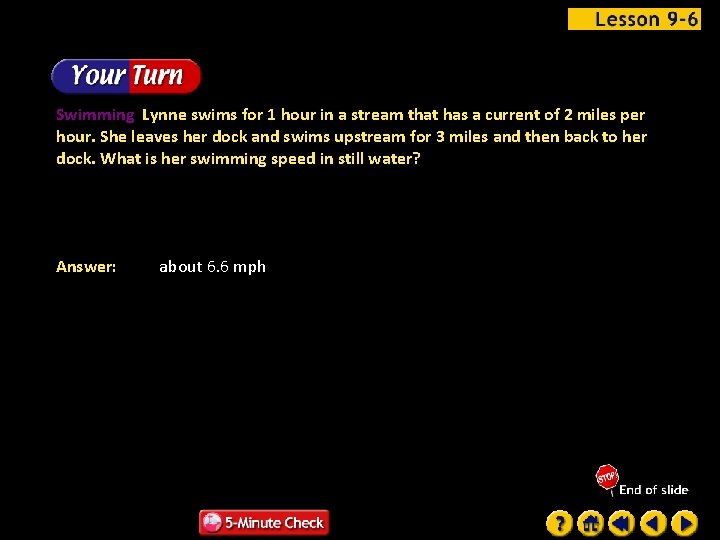
Swimming Lynne swims for 1 hour in a stream that has a current of 2 miles per hour. She leaves her dock and swims upstream for 3 miles and then back to her dock. What is her swimming speed in still water? Answer: about 6. 6 mph

Solve Step 1 Values that make the denominator equal to 0 are excluded from the denominator. For this inequality the excluded value is 0. Step 2 Solve the related equation. Related equation

Multiply each side by 9 s. Simplify. Add. Divide each side by 6.

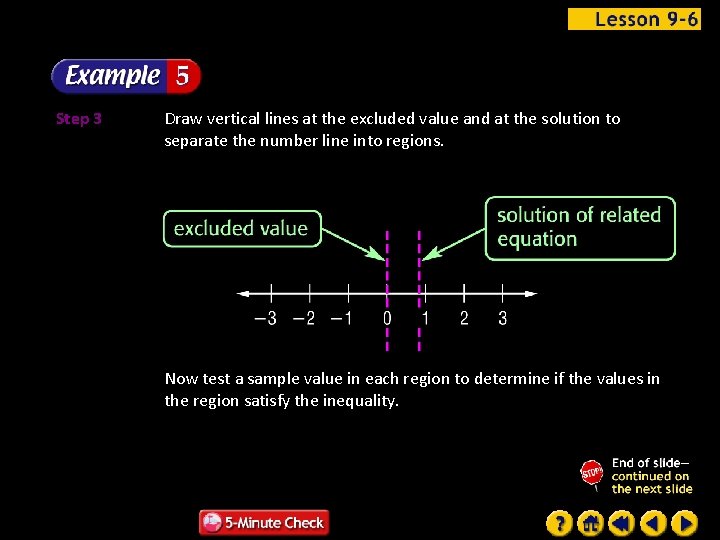
Step 3 Draw vertical lines at the excluded value and at the solution to separate the number line into regions. Now test a sample value in each region to determine if the values in the region satisfy the inequality.

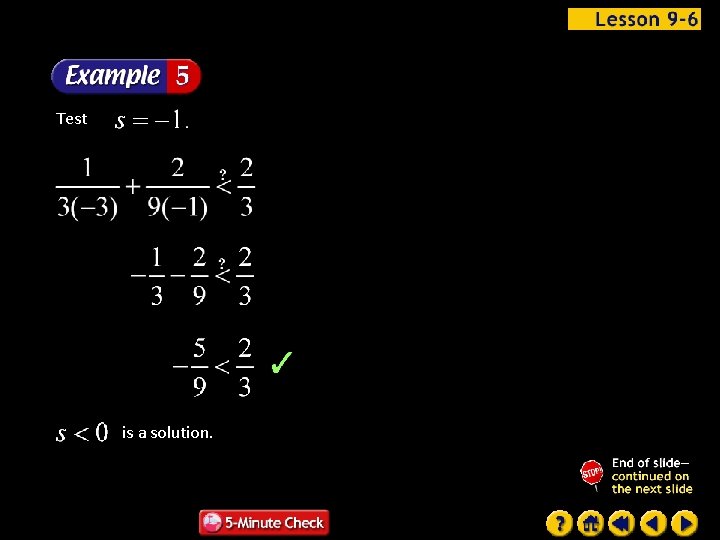
Test is a solution.

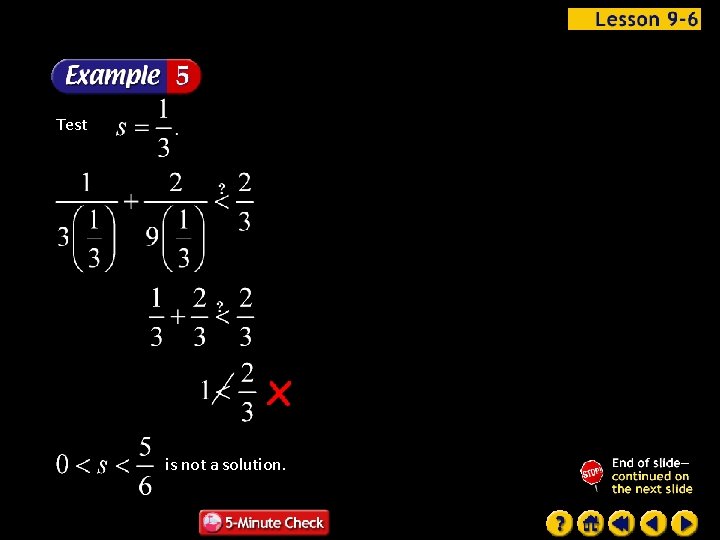
Test is not a solution.

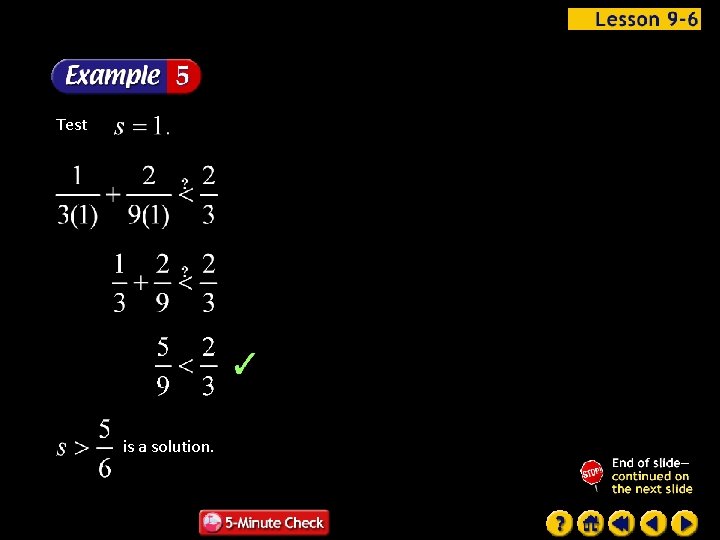
Test is a solution.

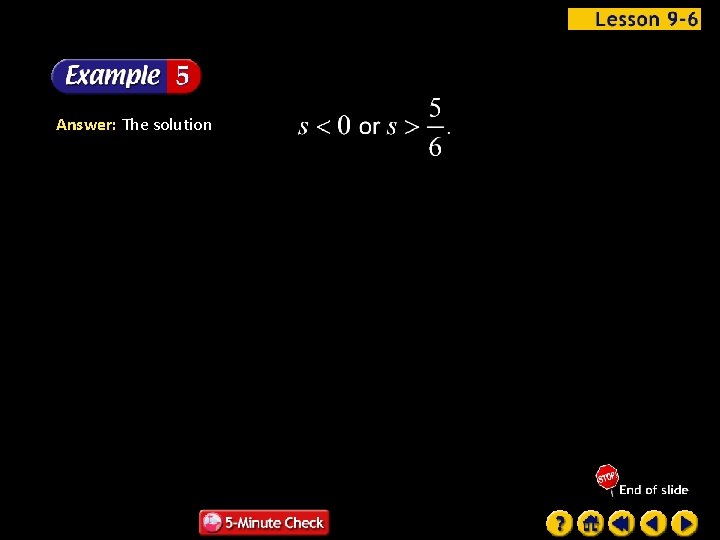
Answer: The solution

Solve Answer: