Statistical Test for Population Mean In statistical testing





















- Slides: 32

Statistical Test for Population Mean • • In statistical testing, we use deductive reasoning to specify what should happen if the conjecture or null hypothesis is true. A study is designed to collect data to challenge this hypothesis. We determine if what we expected to happen is supported by the data. • If it is not supported, we reject the conjecture. • If it cannot be rejected we (tentatively) fail to reject the conjecture. We have not proven the conjecture, we have simply not been able to disprove it with these data. 1

Logic Behind Statistical Tests Statistical tests are based on the concept of Proof by Contradiction. If P then Q = If NOT Q then NOT P Analogy with justice system Court of Law 1. Start with premise that person is innocent. (Opposite is guilty. ) 2. If enough evidence is found to show beyond reasonable doubt that person committed crime, reject premise. (Enough evidence that person is guilty. ) 3. If not enough evidence found, we don’t reject the premise. (Not enough evidence to conclude person guilty. ) Statistical Hypothesis Test 1. Start with null hypothesis, status quo. (Opposite is alternative hypothesis. ) 2. If a significant amount of evidence is found to refute null hypothesis, reject it. (Enough evidence to conclude alternative is true. ) 3. If not enough evidence found, we don’t reject the null. (Not enough evidence to disprove null. ) 2

Examples in Testing Logic CLAIM: A new variety of turf grass has been developed that is claimed to resist drought better than currently used varieties. CONJECTURE: The new variety resists drought no better than currently used varieties. DEDUCTION: If the new variety is no better than other varieties (P), then areas planted with the new variety should display the same number of surviving individuals (Q) after a fixed period without water than areas planted with other varieties. CONCLUSION: If more surviving individuals are observed for the new varieties than the other varieties (NOT Q), then we conclude the new variety is indeed not the same as the other varieties, but in fact is better (NOT P). 3

Five Parts of a Statistical Test 1. Null Hypothesis (H 0: ) 2. Alternative Hypothesis (HA: ) 3. Test Statistic (T. S. ) Computed from sample data. Sampling distribution is known if the Null Hypothesis is true. 4. Rejection Region (R. R. ) Reject H 0 if the test statistic computed with the sample data is unlikely to come from the sampling distribution under the assumption that the Null Hypothesis is true. 5. Conclusion: Reject H 0 or Do Not Reject H 0 Other HA: < 530 H 0: ≤ 530 HA: > 530 R. R. z* > z Or z* < -z Or | z*| > z /2 4

Hypotheses Research Hypotheses: The thing we are primarily interested in “proving”. Average height of the class Null Hypothesis: Things are what they say they are, status quo. (It’s common practice to always write H 0 in this way, even though what is meant is the opposite of HA in each case. ) 5

Test Statistic Some function of the data that uses estimates of the parameters we are interested in and whose sampling distribution is known when we assume the null hypothesis is true. Most good test statistics are constructed using some form of a sample mean. The Central Why? Limit Theorem Of Statistics 6

Developing a Test Statistic for the Population Mean Hypotheses of interest: Test Statistic: Sample Mean Under H 0: the sample mean has a sampling distribution that is normal with mean 0. Under HA: the sample mean has a sampling distribution that is also normal but with a mean 1 that is different from 0. 7

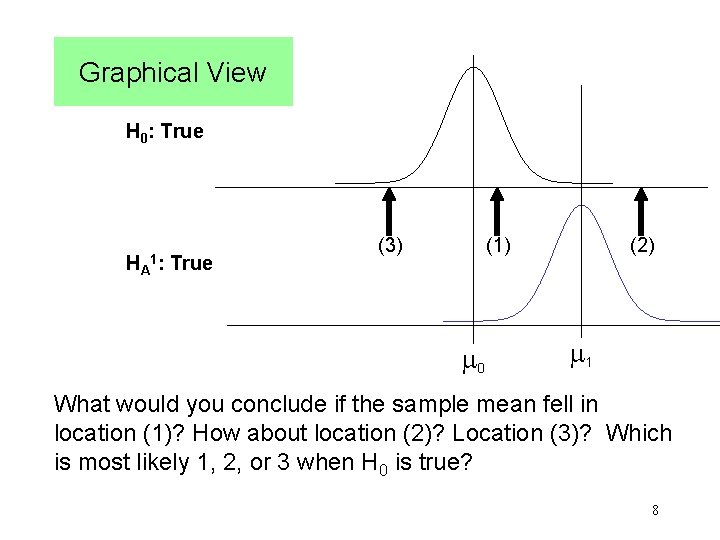
Graphical View H 0: True HA 1: True (3) (1) 0 (2) 1 What would you conclude if the sample mean fell in location (1)? How about location (2)? Location (3)? Which is most likely 1, 2, or 3 when H 0 is true? 8

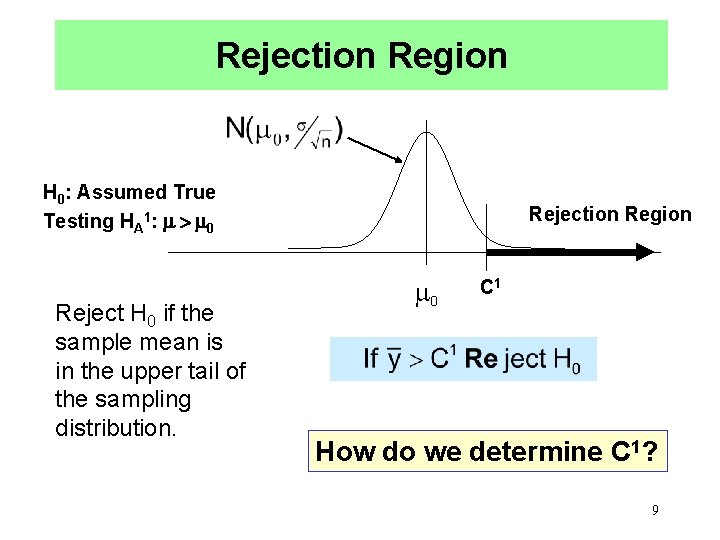
Rejection Region H 0: Assumed True Testing HA 1: > 0 Reject H 0 if the sample mean is in the upper tail of the sampling distribution. Rejection Region 0 C 1 How do we determine C 1? 9

Determining the Critical Value for the Rejection Region Reject H 0 if the sample mean is larger than “expected”. If H 0 were true, we would expect 95% of sample means to be less than the upper limit of a 90% CI for μ. From the standard normal table. In this case, if we use this critical value, in 5 out of 100 repetitions of the study we would reject Ho incorrectly. That is, we would make an error. But, suppose HA 1 is the true situation, then most sample means will be greater than C 1 and we will be making the correct decision to reject more often. 10

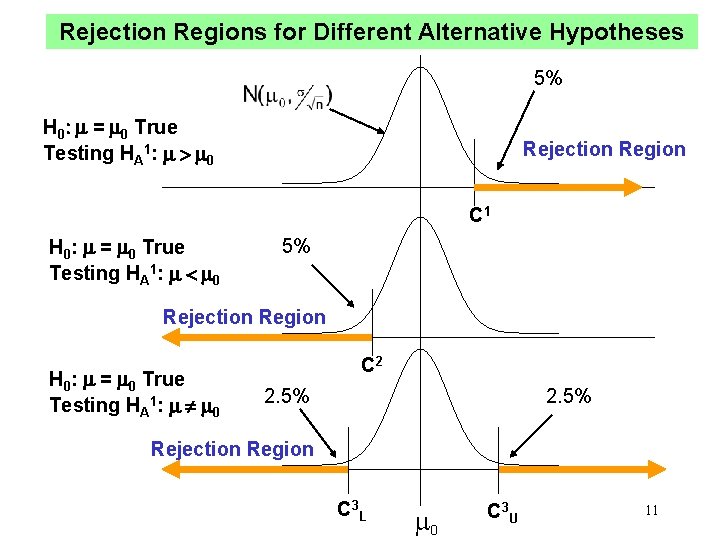
Rejection Regions for Different Alternative Hypotheses 5% H 0: = 0 True Testing HA 1: > 0 Rejection Region C 1 H 0: = 0 True Testing HA 1: < 0 5% Rejection Region H 0: = 0 True Testing HA 1: 0 C 2 2. 5% Rejection Region C 3 L 0 C 3 U 11

Type I Error H 0: True If the sample mean is at location (1) or (3) we make the correct decision. Rejection Region 0 (3) C 1 (1) (2) If the sample mean is at location (2) and H 0 is actually true, we make the wrong decision. This is called making a TYPE I error, and the probability of making this error is usually denoted by the Greek letter . = P(Reject H 0 when H 0 is is the true condition) If then = 1/20=5/100 or. 05 If then the Type I error is . 12

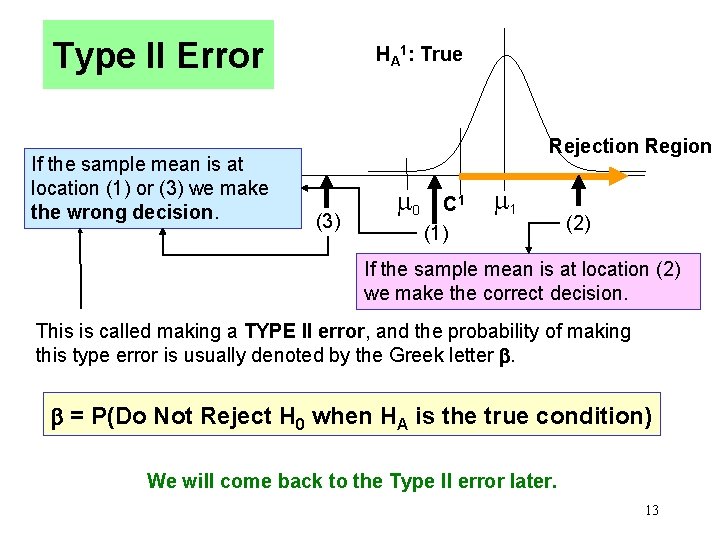
Type II Error If the sample mean is at location (1) or (3) we make the wrong decision. HA 1: True Rejection Region (3) 0 C 1 (1) 1 (2) If the sample mean is at location (2) we make the correct decision. This is called making a TYPE II error, and the probability of making this type error is usually denoted by the Greek letter . = P(Do Not Reject H 0 when HA is the true condition) We will come back to the Type II error later. 13

Type I and II Errors Type I Error Region H 0: True Type II Error Region HA 1: True • We want to minimize the Type I error, just in case H 0 is true, and we wish to minimize the Type II error just in case HA is true. • Problem: A decrease in one causes an increase in the other. • Also: We can never have a Type I or II error equal to zero! 1 0 Rejection Region C 1 14

Setting the Type I Error Rate The solution to our quandary is to set the Type I Error Rate to be small, and hope for a small Type II error also. The logic is as follows: 1. Assume the data come from a population with unknown distribution but which has mean ( ) and standard deviation ( ). 2. For any sample of size n from this population we can compute a sample mean, . 3. Sample means from repeated studies having samples of size n will have the sampling distribution of following a normal distribution with mean and a standard deviation of / n (the standard error of the mean). This is the Central Limit Theorem. 4. If the Null Hypothesis is true and = 0, then we deduce that with probability we will observe a sample mean greater than 0 + z / n. (For example, for = 0. 05, z =1. 645. ) 15

Setting Rejection Regions for Given Type I Error Following this same logic, rejection rules for all three possible alternative hypotheses can be derived. Reject Ho if: Note: It is just easier to work with a test statistic that is standardized. We only need the standard normal table to find critical values. For (1 - )100% of repeated studies, if the true population mean is 0 as conjectured by H 0, then the decision concluded from the statistical test will be correct. On the other hand, in 100% of studies, the wrong decision (a Type I error) will be made. 16

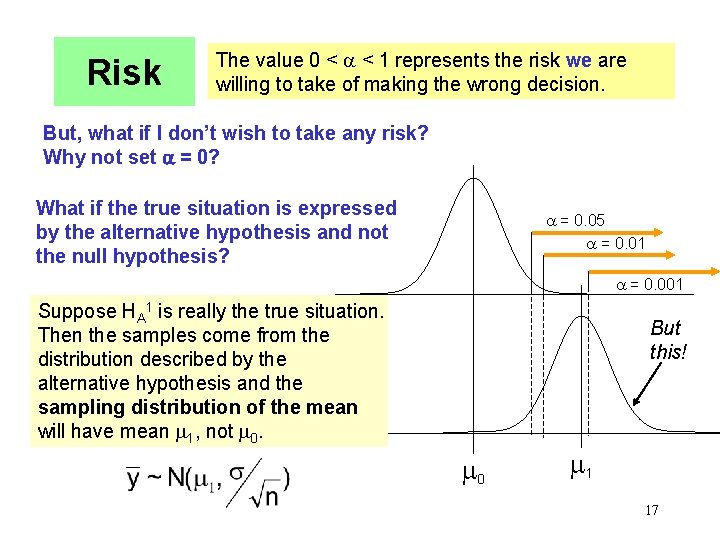
Risk The value 0 < < 1 represents the risk we are willing to take of making the wrong decision. But, what if I don’t wish to take any risk? Why not set = 0? What if the true situation is expressed by the alternative hypothesis and not the null hypothesis? = 0. 05 = 0. 01 = 0. 001 Suppose HA 1 is really the true situation. Then the samples come from the distribution described by the alternative hypothesis and the sampling distribution of the mean will have mean 1, not 0. But this! 0 1 17

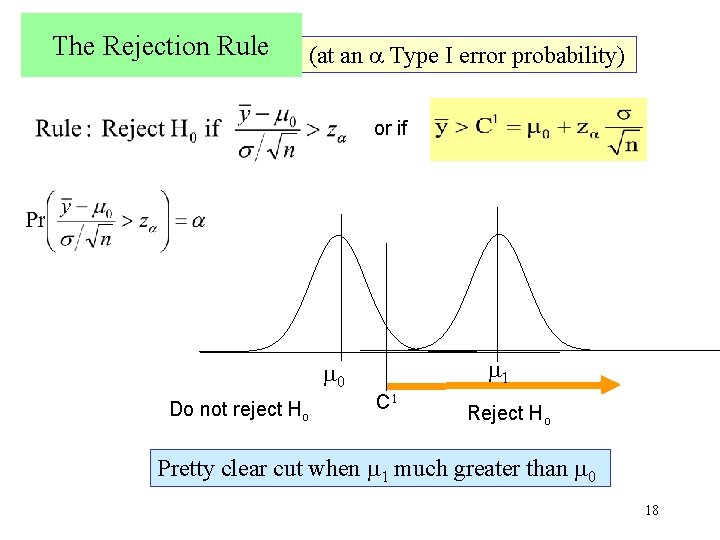
The Rejection Rule (at an Type I error probability) or if 0 Do not reject Ho 1 C 1 Reject Ho Pretty clear cut when 1 much greater than 0 18

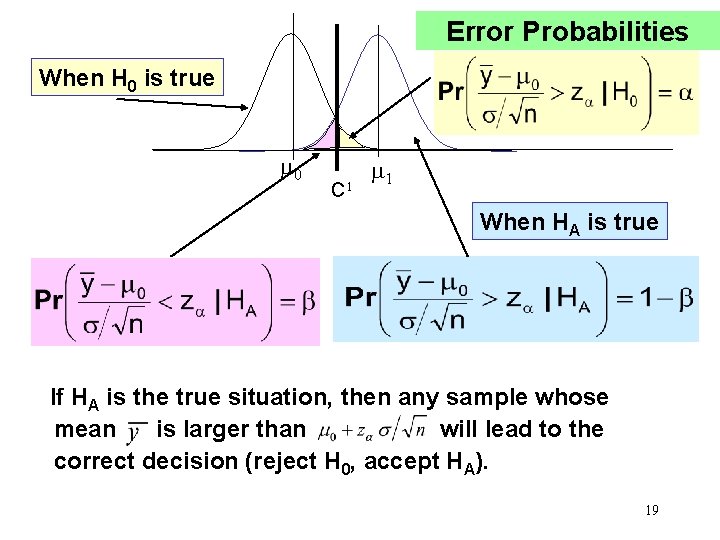
Error Probabilities When H 0 is true 0 C 1 1 When HA is true If HA is the true situation, then any sample whose mean is larger than will lead to the correct decision (reject H 0, accept HA). 19

If HA is the true situation Then any sample such that its sample mean is less than will lead to the wrong decision (do not reject H 0, reject HA). True Situation Reject HA Do not reject HA C 1 Reject H 0 Decision Accept H 0 : True HA : True Type I Error Correct 1 - Correct Type II Error 1 - 20

Computing Error Probabilities Type I Error Probability (Reject H 0 when H 0 true) Power of the test. (Reject H 0 when HA true) Type II Error Probability (Reject HA when HA true) 21

Example Size: n = 50 Sample Mean: Sample Standard deviation: s = 5. 6 H 0: = 0 = 38 HA: > 38 What risk are we willing to take that we reject H 0 when in fact H 0 is true? P(Type I Error) = =. 05 Critical Value: z. 05 = 1. 645 Rejection Region Conclusion: Reject H 0 22

Type II Error. To compute the Type II error for a hypothesis test, we need to have a specific alternative hypothesis stated, rather than a vague alternative Vague HA : > 0 HA : < 0 HA : 0 HA: 10 Specific Note: HA : = 1 > 0 As the difference between 0 and 1 gets larger, the probability of committing a Type II error ( ) decreases. HA : = 1 < 0 HA: = 5 < 10 HA: = 20 > 10 Significant Difference: = 0 - 1 23

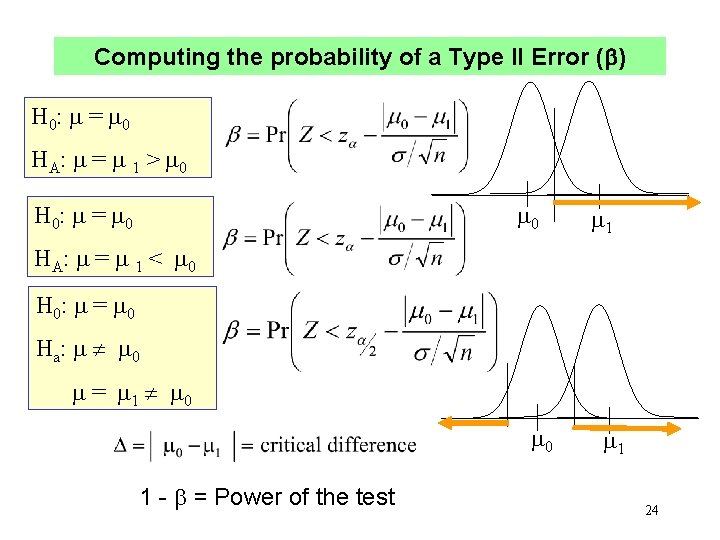
Computing the probability of a Type II Error ( ) H 0: = 0 H A: = 1 > 0 0 H 0: = 0 1 H A: = 1 < 0 H 0: = 0 Ha : 0 = 1 0 0 1 - = Power of the test 1 24

Example: Power Assuming s is actually equal to (usually what is done): 25

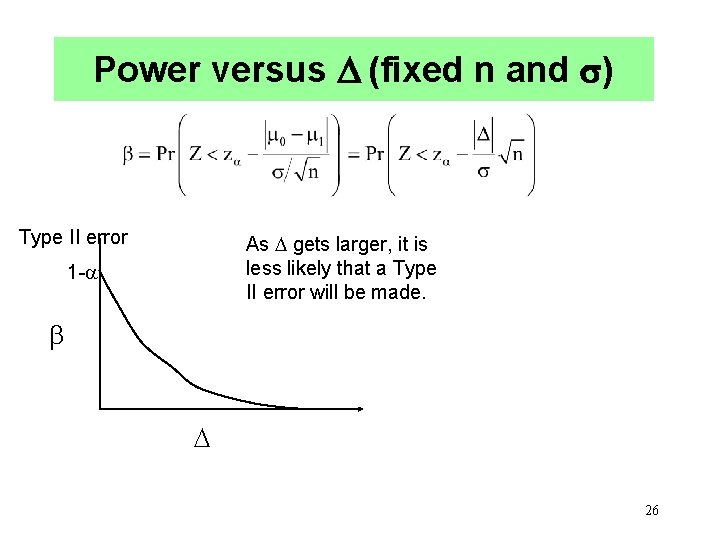
Power versus (fixed n and ) Type II error As gets larger, it is less likely that a Type II error will be made. 1 - 26

Power versus n (fixed and ) Type II error As n gets larger, it is less likely that a Type II error will be made. 1 - n What happens for larger ? 27

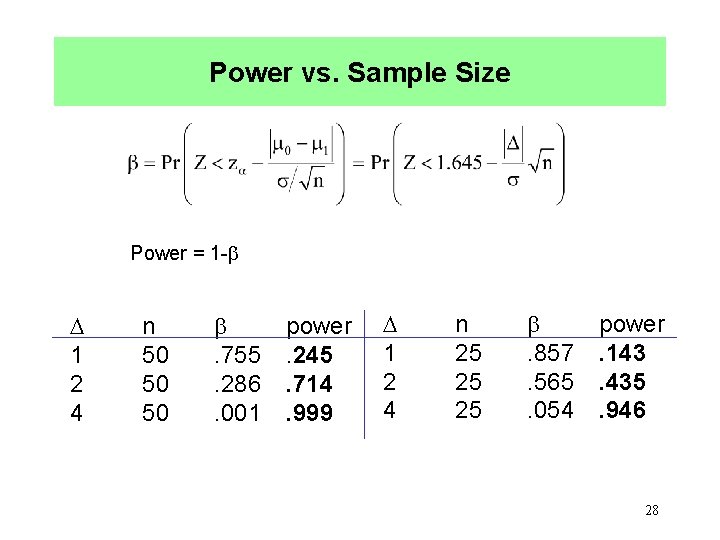
Power vs. Sample Size Power = 1 - 1 2 4 n 50 50 50 . 755. 286. 001 power. 245. 714. 999 1 2 4 n 25 25 25 . 857. 565. 054 power. 143. 435. 946 28

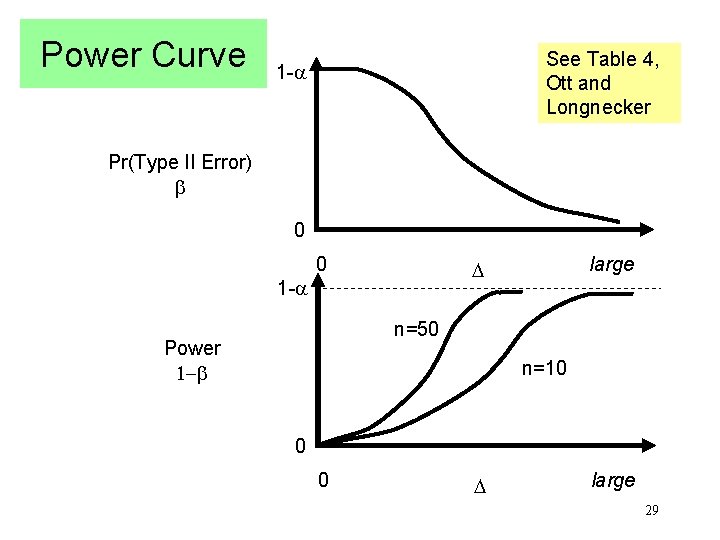
Power Curve See Table 4, Ott and Longnecker 1 - Pr(Type II Error) 0 0 large 1 - n=50 Power 1 - n=10 0 0 large 29

Summary 1) For fixed and n, decreases (power increases) as increases. 2) For fixed and , decreases (power increases) as n increases. 3) For fixed and n, decreases (power increases) as decreases. 30

N( 0, / n) Increasing Precision for fixed increases Power 1 < Decreasing decreases the spread in the sampling dist of N( 0, 1 / n) Note: z changes. Same thing happens if you increase n. Same thing happens if is increased. 31

Sample Size Determination 1) Specify the critical difference, (assume is known). 2) Choose P(Type I error) = and Pr(Type II error) = based on traditional and/or personal levels of risk. 3) One-sided tests: 4) Two-sided tests: Example: One-sided test, = 5. 6, and we wish to show a difference of =. 5 as significant (i. e. reject H 0: = 0 for HA: = 1= 0 + ) with =. 05 and =. 2. 32
 Difference population and sample
Difference population and sample How to find population mean
How to find population mean Chapter 4 population ecology section 1 population dynamics
Chapter 4 population ecology section 1 population dynamics Section 1 population dynamics
Section 1 population dynamics Population ecology section 1 population dynamics
Population ecology section 1 population dynamics Population ecology chapter 4 answers
Population ecology chapter 4 answers Hypothesis in statistics
Hypothesis in statistics Hypothesis testing for population proportion
Hypothesis testing for population proportion Importance of statistical investigation
Importance of statistical investigation Population mean
Population mean How to get population mean
How to get population mean The population mean μ is called: *
The population mean μ is called: * One sample z interval formula
One sample z interval formula Confidence interval for population mean
Confidence interval for population mean Zinterval
Zinterval Population mean example
Population mean example Example of population mean
Example of population mean Population mean
Population mean Sample standard deviation
Sample standard deviation Calculate the mean absolute deviation
Calculate the mean absolute deviation Wvu stat 211
Wvu stat 211 What is domain
What is domain Kv charts in software testing
Kv charts in software testing Data flow testing strategies in software testing
Data flow testing strategies in software testing Positive negative testing
Positive negative testing Cs3250
Cs3250 Globalization testing example
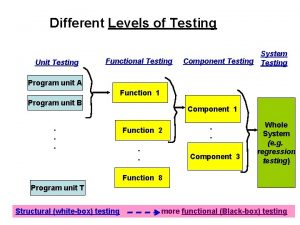
Globalization testing example Functional testing vs unit testing
Functional testing vs unit testing Decision table testing in software testing
Decision table testing in software testing Control structure testing in software engineering
Control structure testing in software engineering Decision table testing in software testing
Decision table testing in software testing Decision table technique
Decision table technique Error yang dapat diketahui dari pengujian black box adalah
Error yang dapat diketahui dari pengujian black box adalah