STATISTICAL INFERENCE PART I POINT ESTIMATION 1 STATISTICAL

STATISTICAL INFERENCE PART I POINT ESTIMATION 1

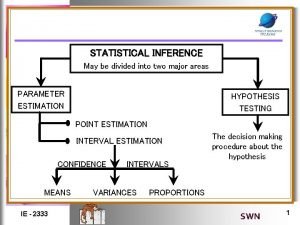
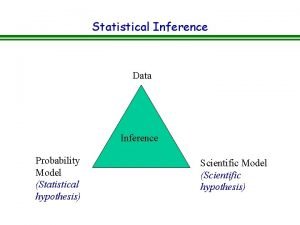
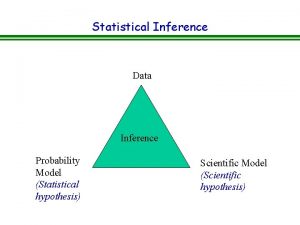
STATISTICAL INFERENCE • Determining certain unknown properties of a probability distribution on the basis of a sample (usually, a r. s. ) obtained from that distribution Point Estimation: Interval Estimation: Hypothesis Testing: ( ) 2

STATISTICAL INFERENCE • Parameter Space ( ): The set of all possible values of an unknown parameter, ; . • A pdf with unknown parameter: f(x; ), . • Estimation: Where in , is likely to be? { f(x; ), } The family of pdfs 3

STATISTICAL INFERENCE • Statistic: A function of rvs (usually a sample rvs in an estimation) which does not contain any unknown parameters. • Estimator of an unknown parameter : A statistic used for estimating . An observed value 4

METHODS OF ESTIMATION Method of Moments Estimation, Maximum Likelihood Estimation 5

METHOD OF MOMENTS ESTIMATION (MME) • Let X 1, X 2, …, Xn be a r. s. from a population with pmf or pdf f(x; 1, 2, …, k). The MMEs are found by equating the first k population moments to corresponding sample moments and solving the resulting system of equations. Population Moments Sample Moments 6

METHOD OF MOMENTS ESTIMATION (MME) so on… Continue this until there are enough equations to solve for the unknown parameters. 7

EXAMPLES • Let X~Exp( ). • For a r. s of size n, find the MME of . • For the following sample (assuming it is from Exp( )), find the estimate of : 11. 37, 3, 0. 15, 4. 27, 2. 56, 0. 59. 8

EXAMPLES • Let X~N(μ, σ²). For a r. s of size n, find the MMEs of μ and σ². • For the following sample (assuming it is from N(μ, σ²)), find the estimates of μ and σ²: 4. 93, 6. 82, 3. 12, 7. 57, 3. 04, 4. 98, 4. 62, 4. 84, 2. 95, 4. 22 9

DRAWBACKS OF MMES • Although sometimes parameters are positive valued, MMEs can be negative. • If moments does not exist, we cannot find MMEs. 10

MAXIMUM LIKELIHOOD ESTIMATION (MLE) • Let X 1, X 2, …, Xn be a r. s. from a population with pmf or pdf f(x; 1, 2, …, k), the likelihood function is defined by 11

MAXIMUM LIKELIHOOD ESTIMATION (MLE) • For each sample point (x 1, …, xn), let be a parameter value at which L( 1, …, k| x 1, …, xn) attains its maximum as a function of ( 1, …, k), with (x 1, …, xn) held fixed. A maximum likelihood estimator (MLE) of parameters ( 1, …, k) based on a sample (X 1, …, Xn) is • The MLE is the parameter point for which the observed sample is most likely. 12

EXAMPLES • Let X~Bin(n, p). One observation on X is available, and it is known that n is either 2 or 3 and p=1/2 or 1/3. Our objective is to estimate the pair (n, p). x 0 (2, 1/2) 1/4 (2, 1/3) 4/9 (3, 1/2) 1/8 (3, 1/3) 8/27 Max. Prob. 4/9 1 1/2 4/9 3/8 12/27 1/2 2 1/4 1/9 3/8 6/27 3/8 3 0 0 1/8 1/27 1/8 13

MAXIMUM LIKELIHOOD ESTIMATION (MLE) • It is usually convenient to work with the logarithm of the likelihood function. • Suppose that f(x; 1, 2, …, k) is a positive, differentiable function of 1, 2, …, k. If a supremum exists, it must satisfy the likelihood equations • MLE occurring at boundary of cannot be obtained by differentiation. So, use inspection. 14

MLE • Moreover, you need to check that you are in fact maximizing the log-likelihood (or likelihood) by checking that the second derivative is negative. 15

EXAMPLES 1. X~Exp( ), >0. For a r. s of size n, find the MLE of . 16

EXAMPLES 2. X~N( , 2). For a r. s. of size n, find the MLEs of and 2. 17

EXAMPLES 3. X~Uniform(0, ), >0. For a r. s of size n, find the MLE of . 18

INVARIANCE PROPERTY OF THE MLE • If is the MLE of , then for any function ( ), the MLE of ( ) is. Example: X~N( , 2). For a r. s. of size n, the MLE of is. By the invariance property of MLE, the MLE of 2 is 19

ADVANTAGES OF MLE • Often yields good estimates, especially for large sample size. • Usually they are consistent estimators. • Invariance property of MLEs • Asymptotic distribution of MLE is Normal. • Most widely used estimation technique. 20

DISADVANTAGES OF MLE • Requires that the pdf or pmf is known except the value of parameters. • MLE may not exist or may not be unique. • MLE may not be obtained explicitly (numerical or search methods may be required. ). It is sensitive to the choice of starting values when using numerical estimation. • MLEs can be heavily biased for small samples. • The optimality properties may not apply for small samples. 21

SOME PROPERTIES OF ESTIMATORS • UNBIASED ESTIMATOR (UE): An estimator is an UE of the unknown parameter , if Otherwise, it is a Biased Estimator of . Bias of If is UE of , for estimating 22

SOME PROPERTIES OF ESTIMATORS • ASYMPTOTICALLY UNBIASED ESTIMATOR (AUE): An estimator is an AUE of the unknown parameter , if 23

SOME PROPERTIES OF ESTIMATORS • CONSISTENT ESTIMATOR (CE): An estimator which converges in probability to an unknown parameter for all is called a CE of . For large n, a CE tends to be closer to the unknown population parameter. • MLEs are generally CEs. 24

EXAMPLE For a r. s. of size n, By WLLN, 25

MEAN SQUARED ERROR (MSE) • The Mean Square Error (MSE) of an estimator for estimating is If is smaller, estimator of . is the better 26

MEAN SQUARED ERROR CONSISTENCY • Tn is called mean squared error consistent (or consistent in quadratic mean) if E{Tn }2 0 as n . Theorem: Tn is consistent in MSE iff i) Var(Tn) 0 as n . • If E{Tn }2 0 as n , Tn is also a CE of . 27

EXAMPLES X~Exp( ), >0. For a r. s of size n, consider the following estimators of , and discuss their bias and consistency. Which estimator is better? 28