Sorted Lists CS 308 Data Structures Sorted List

Sorted Lists CS 308 - Data Structures

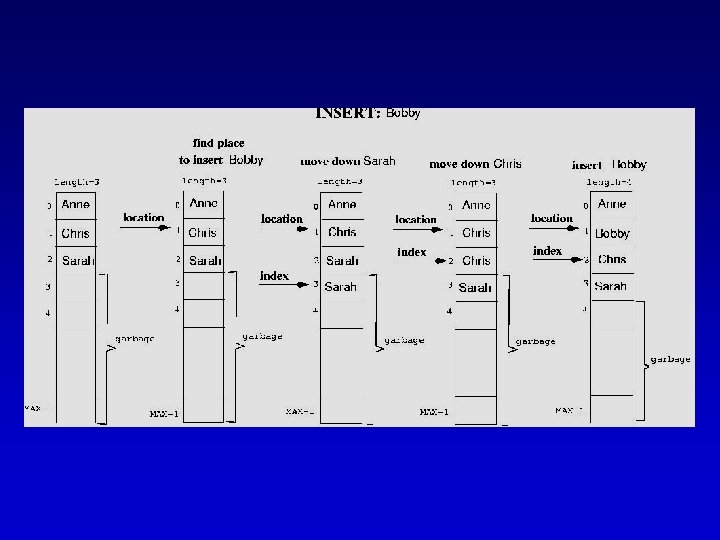
Sorted List Specification (partial) Insert. Item (Item. Type item) Function: Adds item to list Preconditions: (1) List has been initialized, (2) List is not full, (3) item is not in list (4) List is sorted by key member. Postconditions: (1) item is in list, (2) List is still sorted.

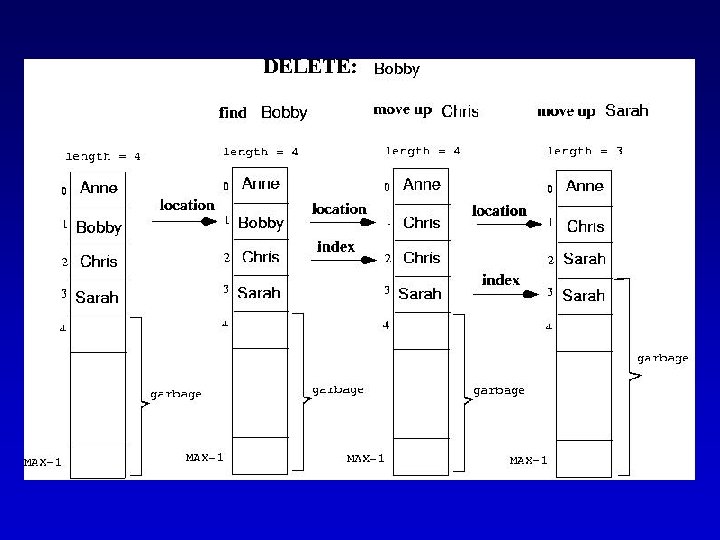
Sorted List Specification (partial) Delete. Item(Item. Type item) Function: Deletes the element whose key matches item's key Preconditions: (1) List has been initialized, (2) Key member of item has been initialized, (3) There is only one element in list which has a key matching item's key, (4) List is sorted by key member. Postconditions: (1) No element in list has a key matching item's key, (2) List is still sorted.

Sorted List Implementation template<class Item. Type> class Sorted. Type { public: void Make. Empty(); bool Is. Full() const; int Length. Is() const; void Retrieve. Item(Item. Type&, bool&); void Insert. Item(Item. Type); void Delete. Item(Item. Type); void Reset. List(); bool Is. Last. Item(); void Get. Next. Item(Item. Type&); private: int length; Item. Type info[MAX_ITEMS]; int current. Pos; };

Sorted List Implementation (cont. ) template<class Item. Type> void Sorted. Type<Item. Type>: : Insert. Item(Item. Type item) { int location = 0; bool found; found = false; while( (location < length) && !found) { } if (item < info[location]) found = true; else location++; (continues)

Sorted List Implementation (cont. ) for (int index = length; index > location; index--) info[index] = info[index - 1]; info[location] = item; length++; }

Sorted List Implementation (cont. ) template<class Item. Type> void Sorted. Type<Item. Type>: : Delete. Item(Item. Type item) { int location = 0; while (item != info[location]) location++; for (int index = location + 1; index < length; index++) info[index - 1] = info[index]; length--; }

Linear Search Algorithm (cont. ) (more efficient when the item we are searching for is not in the list)

Improving Retrieve. Item() Linear Search Algorithm: stop when you pass the place where the item would be if it were there. template<class Item. Type> void Sorted. Type<Item. Type>: : Retrieve. Item (Item. Type& item, bool& found) { int location = 0; found = false; while ( (location < length) && !found) { } if ( item > info[location]) { location++; else if(item < info[location]) location = length; // no reason to continue else { found = true; item = info[location]; }

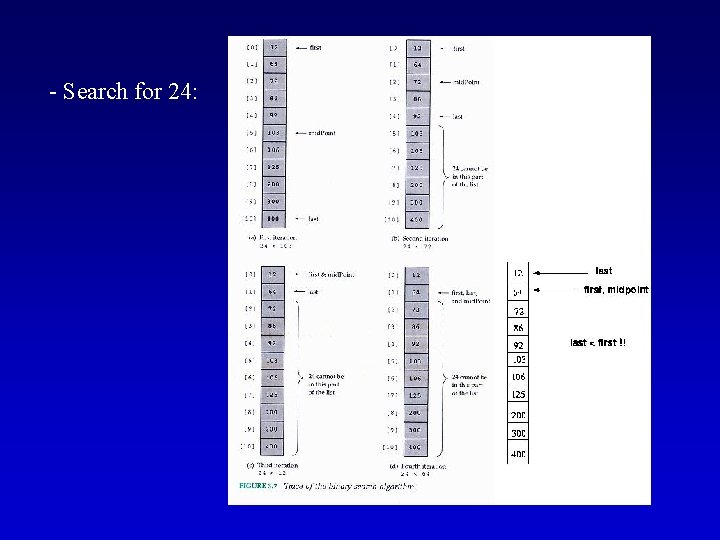
Binary Search Algorithm Split the current search area in half, and if the item is not found there, then search the appropriate half.

- Search for 24:

Binary Search Algorithm (cont. ) template<class Item. Type> void Sorted. Type<Item. Type>: : Retrieve. Item(Item. Type& item, bool found) { int mid. Point; int first = 0; int last = length - 1; found = false; while( (first <= last) && !found) { mid. Point = (first + last) / 2; if (item < info[mid. Point]) last = mid. Point - 1; else if(item > info[mid. Point]) first = mid. Point + 1; else { found = true; item = info[mid. Point]; } } }

Is Binary Search more efficient? • Number of iterations: – For a list of 11 elements, it never executed more than 4 times (e. g. , approximately log 2 11 times)!! – Linear Search, on the other hand, can execute up to 11 times !! Average Number of Iterations Length Linear Search Binary Search 10 5. 5 2. 9 100 50. 5 5. 8 1, 000 500. 5 9. 0 10, 000 5000. 5 12. 0

Is Binary Search more efficient? (cont. ) • Number of computations: – Binary search does more computations than Linear Search • Overall: – If the number of components is small (say, under 20), then Linear Search is faster. – If the number of components is large, then Binary Search is faster.

Analysis of Algorithms What is the goal? • To compare algorithms!! • How running time increases as the size of • the problem increases. Other factors can also be considered (e. g. , memory requirements, programmer's effort etc. )

How do we analyze algorithms? • We need to define a number of objective measures. (1) Compare execution times. Problem: times are specific to a particular computer !! (2) Count the number of statements executed. Problem: number of statements vary with the programming language as well as the style of the individual programmer.

How do we analyze algorithms? (cont. ) Algorithm 1 Algorithm 2 arr[0] = 0; arr[1] = 0; arr[2] = 0; . . . arr[N-1] = 0; for(i=0; i<N; i++) arr[i] = 0;

Order of magnitude • Consider the example of buying elephants and • • goldfish Cost: cost_of_elephants + cost_of_goldfish Cost cost_of_elephants (approximation) The low order terms in a function are relatively insignificant for large n n 4 + 100 n 2 + 10 n + 50 n 4 Or n 4 + 100 n 2 + 10 n + 50 and n 4 have the same rate of growth

Big-O notation • In mathematics, we approximate functions • • • using Big-O notation We say that n 4 + 100 n 2 + 10 n + 50 is of the order of n 4 or O(n 4) We say that 10 n 3 + 2 n 2 is O(n 3) We say that n 3 - n 2 is O(n 3) We say that 10 is O(1), We say that 1273 is O(1)

Big-O notation (cont. ’d) • O(f(N)) is the set of all functions g(N) such that g(N) <= cf(N)

Computing running time • Associate a "cost" with each statement and find the • "total cost“ by finding the total number of times each statement is executed. Express running time in terms of the size of the problem. Algorithm 1 Algorithm 2 Cost c 1 c 1 arr[0] = 0; arr[1] = 0; arr[2] = 0; . . . arr[N-1] = 0; c 1 -----c 1+. . . +c 1 = c 1 x N for(i=0; i<N; i++) arr[i] = 0; Cost c 2 c 1 ------(N+1) x c 2 + N x c 1 = (c 2 + c 1) x N + c 2

Computing running time (cont. ) • Both algorithms are of the same order: O(N) Cost sum = 0; c 1 for(i=0; i<N; i++) c 2 for(j=0; j<N; j++) c 2 sum += arr[i][j]; c 3 ------c 1 + c 2 x (N+1) + c 2 x N x (N+1) + c 3 x N = O(N 2)

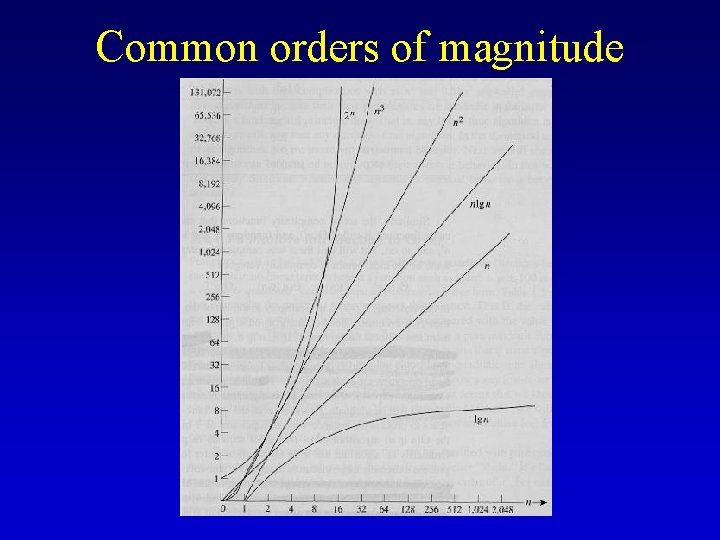
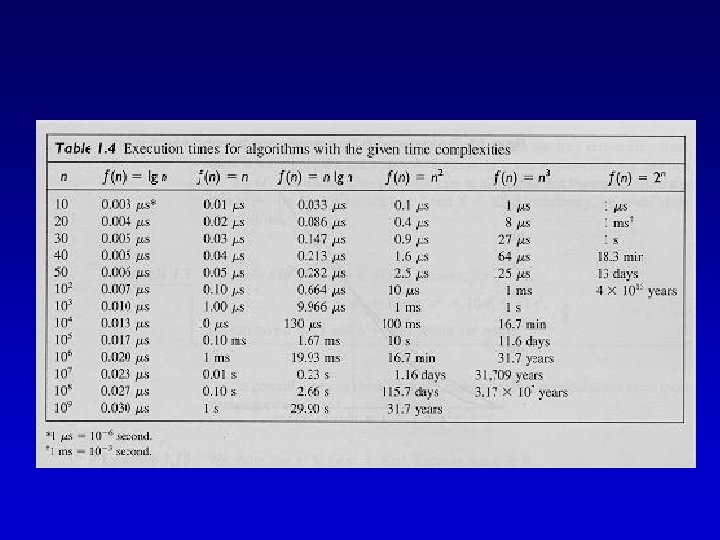
Common orders of magnitude

Running time of various statements

Examples i = 0; while (i<N) { X=X+Y; // O(1) result = mystery(X); // O(N), just an example. . . i++; // O(1) } • The body of the while loop: • Loop is executed: O(N) N times N x O(N) = O(N 2)

Examples (cont. ’d) if (i<j) for ( i=0; i<N; i++ ) X = X+i; else O(1) X=0; O(N) Max ( O(N), O(1) ) = O (N)

Analysis of the Unsorted List Implementation • Make. Empty, Length. Is, and Is. Full take O(1) time. • Reset. List and Get. Next. Item take also O(1) time. • Retrieve. Item takes O(length) time (worst case) • • O(1) time in the best case O(length/2)time in the average case O(length) time in the worst case Insert. Item takes O(1) time Delete. Item takes O(length) time (worst case) Find the item first: O(length) time (worst case) Delete the item: O(1) time

Analysis of the Sorted List Implementation • Make. Empty, Length. Is, and Is. Full take O(1) • • time. Reset. List and Get. Next. Item take also O(1) time. Retrieve. Item takes O(length) time

Linear Search Algorithm template<class Item. Type> void Sorted. Type<Item. Type>: : Retrieve. Item (Item. Type& item, bool& found) { int location = 0; found = false; while ( (location < length) && !found) { if ( item > info[location]) { location++; else if(item < info[location]) location = length; // no reason to continue else { found = true; O(length) item = info[location]; } }

Binary Search Algorithm template<class Item. Type> void Sorted. Type<Item. Type>: : Retrieve. Item(Item. Type& item, bool found) { int mid. Point; int first = 0; int last = length - 1; found = false; while( (first <= last) && !found) { mid. Point = (first + last) / 2; if (item < info[mid. Point]) last = mid. Point - 1; else if(item > info[mid. Point]) first = mid. Point + 1; O(log(length)) else { found = true; item = info[mid. Point]; } } }

- Insert. Item takes O(length) time template<class Item. Type> void Sorted. Type<Item. Type>: : Insert. Item(Item. Type item) { int location = 0; bool found; found = false; while( (location < length) && !found) { if (item < info[location]) found = true; else location++; } for (int index = length; index > location; index--) info[index] = info[index - 1]; info[location] = item; length++; }

- Delete. Item takes O(length) time template<class Item. Type> void Sorted. Type<Item. Type>: : Delete. Item(Item. Type item) { int location = 0; while (item != info[location]) location++; for (int index = location + 1; index < length; index++) info[index - 1] = info[index]; length--; }

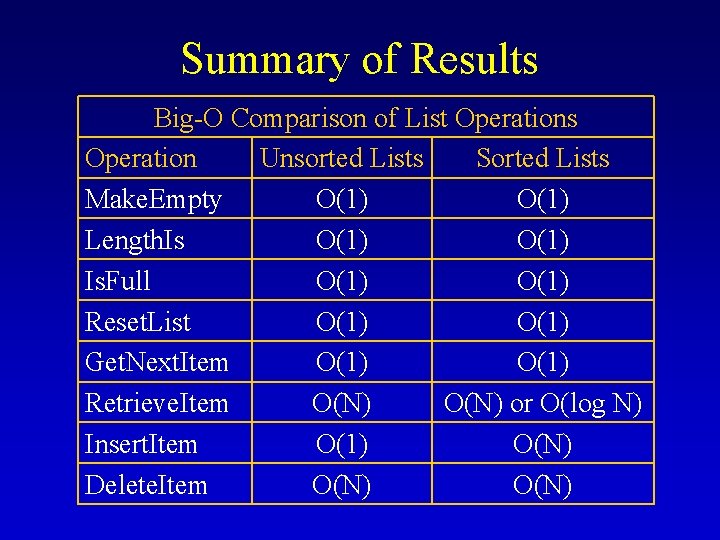
Summary of Results Big-O Comparison of List Operations Operation Unsorted Lists Sorted Lists Make. Empty O(1) Length. Is O(1) Is. Full O(1) Reset. List O(1) Get. Next. Item O(1) Retrieve. Item O(N) or O(log N) Insert. Item O(1) O(N) Delete. Item O(N)

Exercises • 6, 8, 10, 13