LINKED LISTS CSCD 216 Linked Lists Linked Lists

LINKED LISTS CSCD 216 - Linked Lists

Linked Lists • • • Definition of Linked Lists Examples of Linked Lists Operations on Linked Lists Implementations Singly-linked lists Doubly-linked lists CS 103 2

Introduction • When dealing with many problems we need a dynamic list, dynamic in the sense that the size requirement need not be known at compile time. • Thus, the list may grow or shrink during runtime. • A linked list is a data structure that is used to model such a dynamic list of data items, so the study of the linked lists as one of the data structures is important. CSCD 216 - Linked Lists

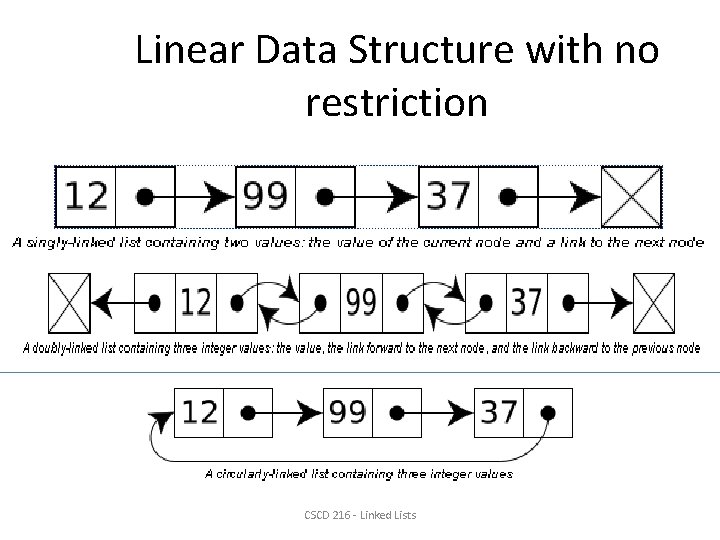
Linear Data Structure with no restriction • Linked list – consists of a sequence of nodes, each containing arbitrary data fields and one or two references ("links") pointing to the next and/or previous nodes CSCD 216 - Linked Lists

Linear Data Structure with no restriction CSCD 216 - Linked Lists

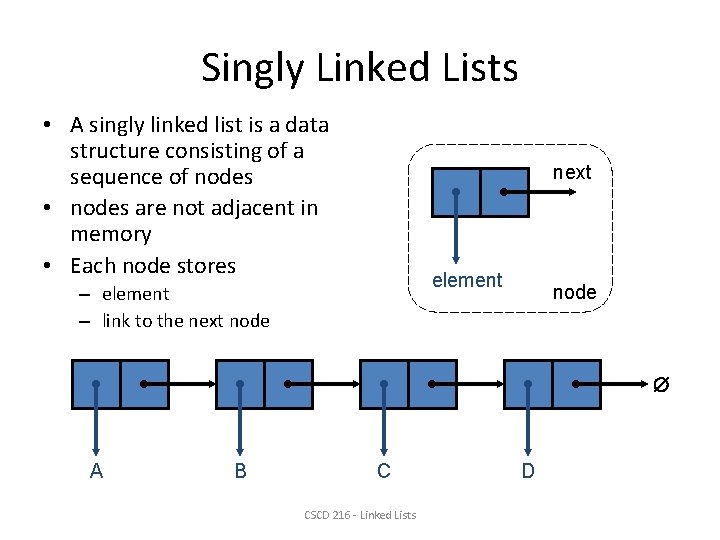
Singly Linked Lists • A singly linked list is a data structure consisting of a sequence of nodes • nodes are not adjacent in memory • Each node stores next element – link to the next node A B C CSCD 216 - Linked Lists D

Definition Details • Each item has a data part (one or more data members), and a link that points to the next item • One natural way to implement the link is as a pointer; that is, the link is the address of the next item in the list • It makes good sense to view each item as an object, that is, as an instance of a class. • We call that class: Node • The last item does not point to anything. We set its link member to NULL. CS 103 7

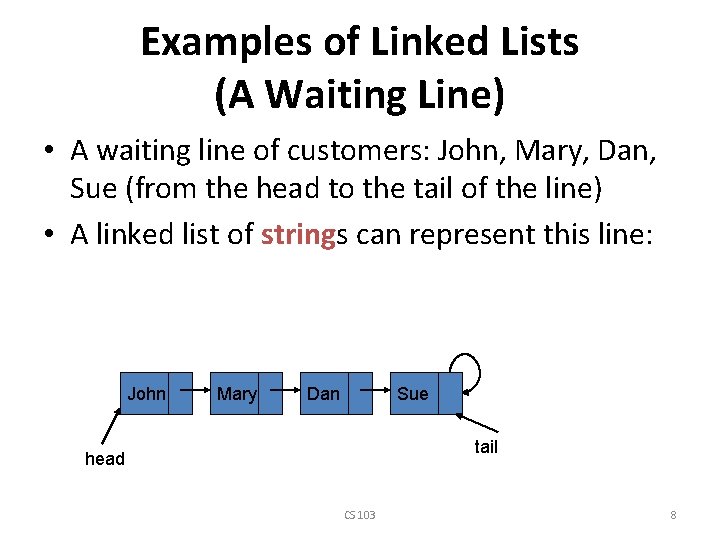
Examples of Linked Lists (A Waiting Line) • A waiting line of customers: John, Mary, Dan, Sue (from the head to the tail of the line) • A linked list of strings can represent this line: John Mary Dan Sue tail head CS 103 8

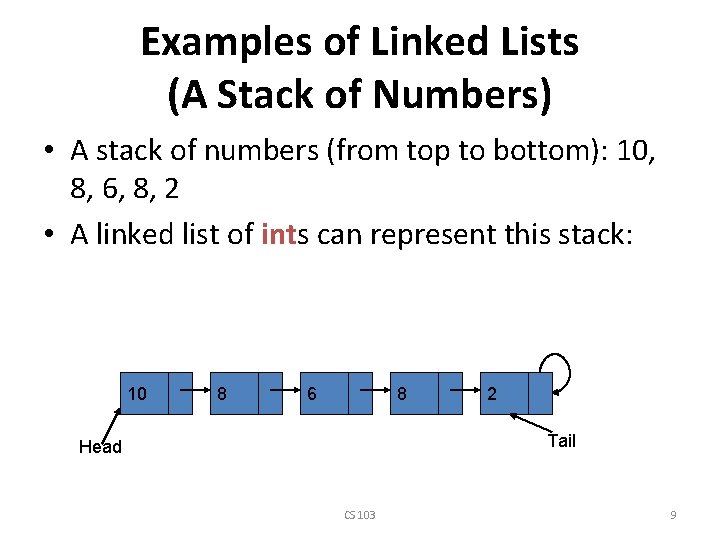
Examples of Linked Lists (A Stack of Numbers) • A stack of numbers (from top to bottom): 10, 8, 6, 8, 2 • A linked list of ints can represent this stack: 10 8 6 8 2 Tail Head CS 103 9

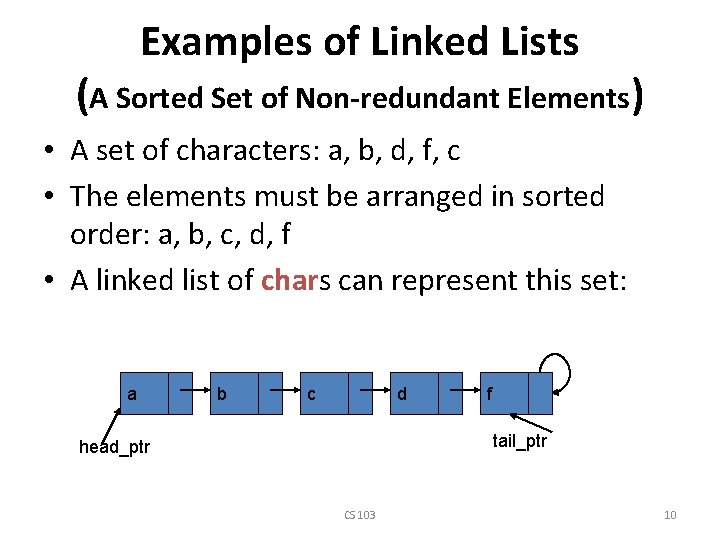
Examples of Linked Lists (A Sorted Set of Non-redundant Elements) • A set of characters: a, b, d, f, c • The elements must be arranged in sorted order: a, b, c, d, f • A linked list of chars can represent this set: a b c d f tail_ptr head_ptr CS 103 10

Examples of Linked Lists (A Polynomial) • A polynomial of degree n is the function Pn(x)=a 0+a 1 x+a 2 x 2+…+anxn. The ai’s are called the coefficients of the polynomial • The polynomial can be represented by a linked list (2 data members and a link per item): a 0, 0 a 1, 1 a 2, 2 an, n tail_ptr head_ptr CS 103 11

Operations on Linked Lists • Insert a new item – At the head of the list, or – At the tail of the list, or – Inside the list, in some designated position • Search for an item in the list – The item can be specified by position, or by some value • Delete an item from the list – Search for and locate the item, then remove the item, and finally adjust the surrounding pointers • size( ); • is. Empty( ) CS 103 12

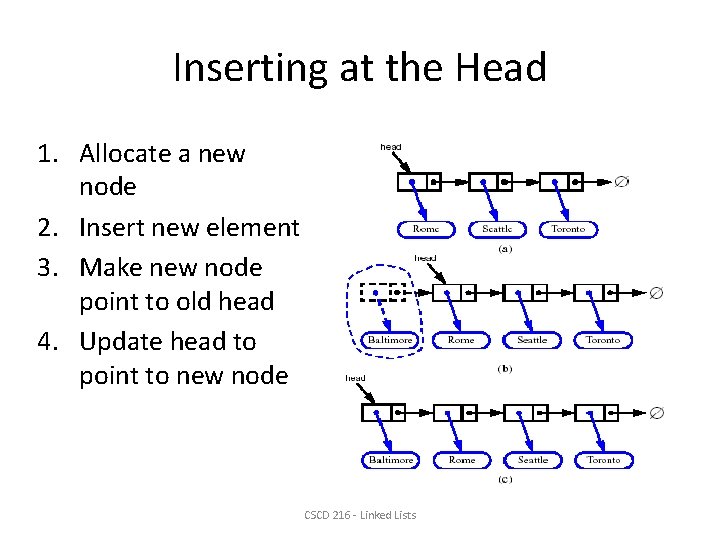
Inserting at the Head 1. Allocate a new node 2. Insert new element 3. Make new node point to old head 4. Update head to point to new node CSCD 216 - Linked Lists

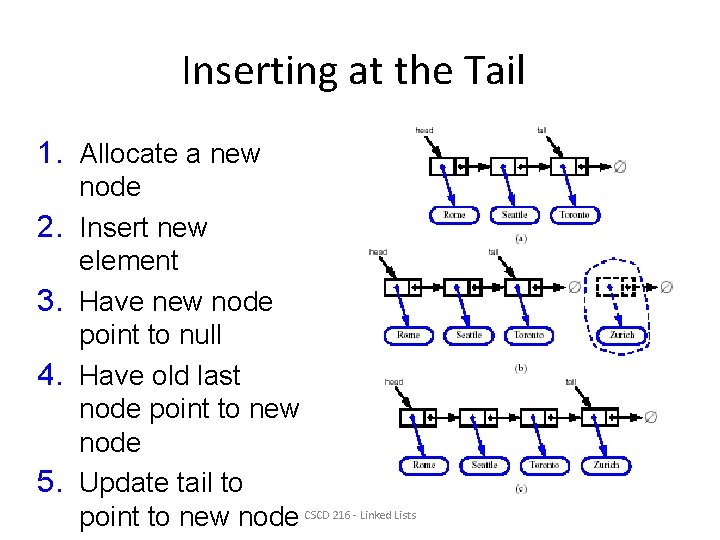
Inserting at the Tail 1. Allocate a new 2. 3. 4. 5. node Insert new element Have new node point to null Have old last node point to new node Update tail to point to new node CSCD 216 - Linked Lists

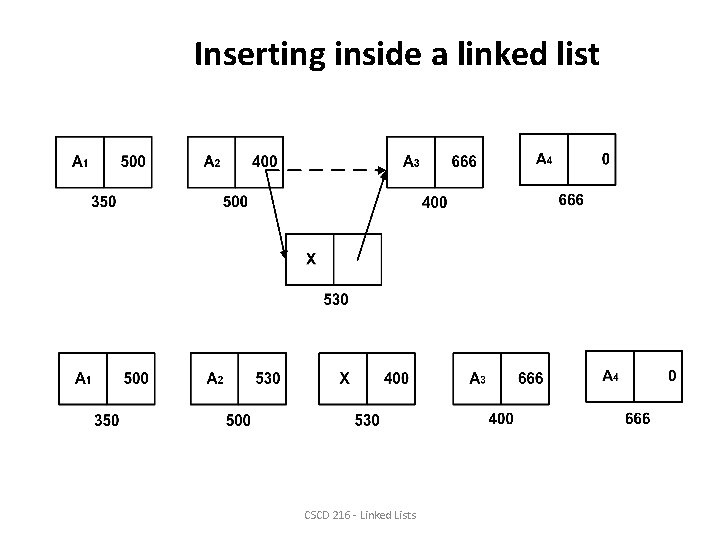
Inserting inside a linked list CSCD 216 - Linked Lists

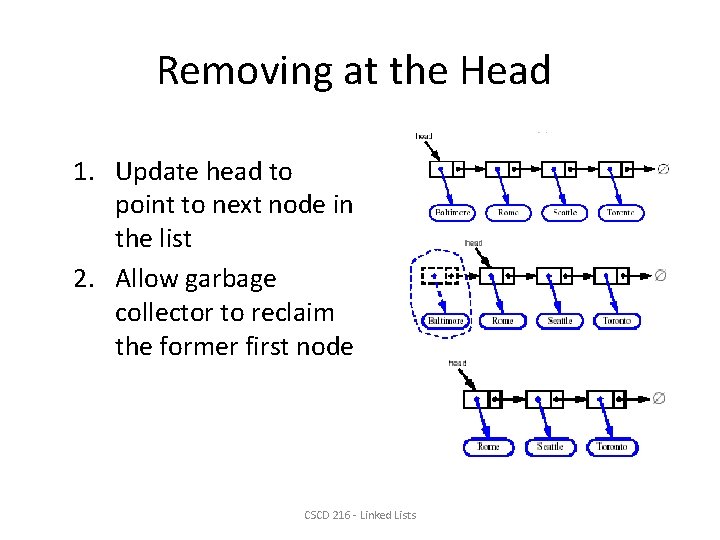
Removing at the Head 1. Update head to point to next node in the list 2. Allow garbage collector to reclaim the former first node CSCD 216 - Linked Lists

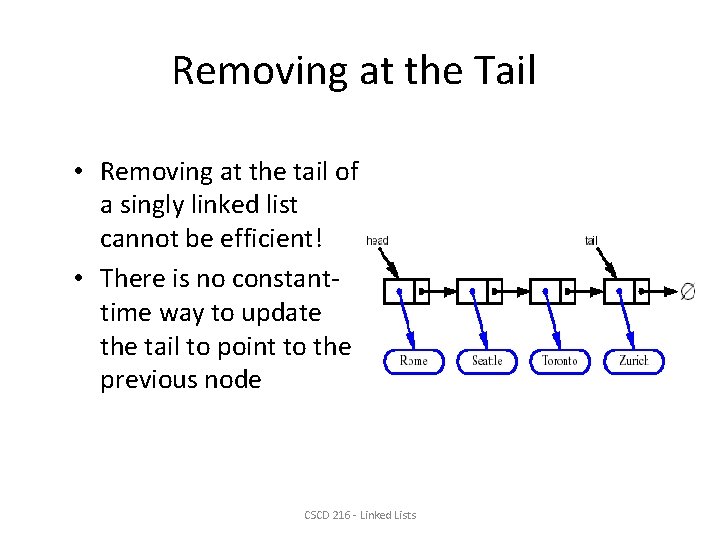
Removing at the Tail • Removing at the tail of a singly linked list cannot be efficient! • There is no constanttime way to update the tail to point to the previous node CSCD 216 - Linked Lists

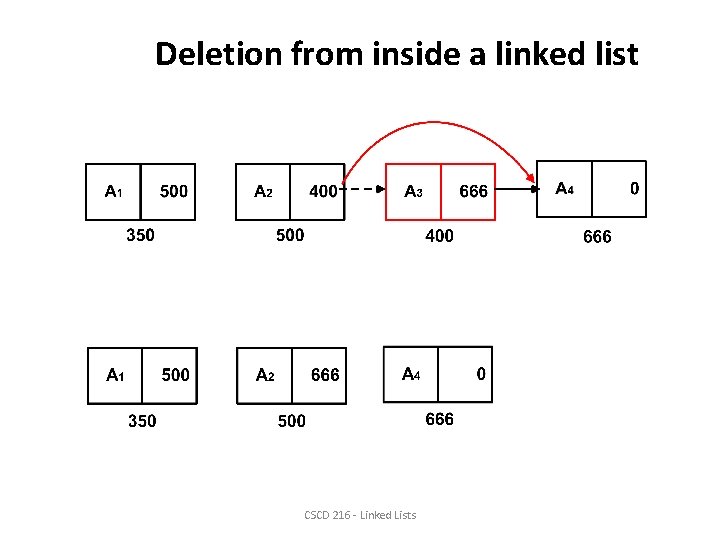
Deletion from inside a linked list CSCD 216 - Linked Lists

Linked List Implementation of Lists • Need to know where the first node is – the rest of the nodes can be accessed • No need to move the list for insertion and deletion operations • No memory waste CSCD 216 - Linked Lists

Linked List Implementation of Lists Linked List Array Traverse List Find O(N) Find. Kth (L, i) O(1) Delete Insert O(1) O(N) CSCD 216 - Linked Lists

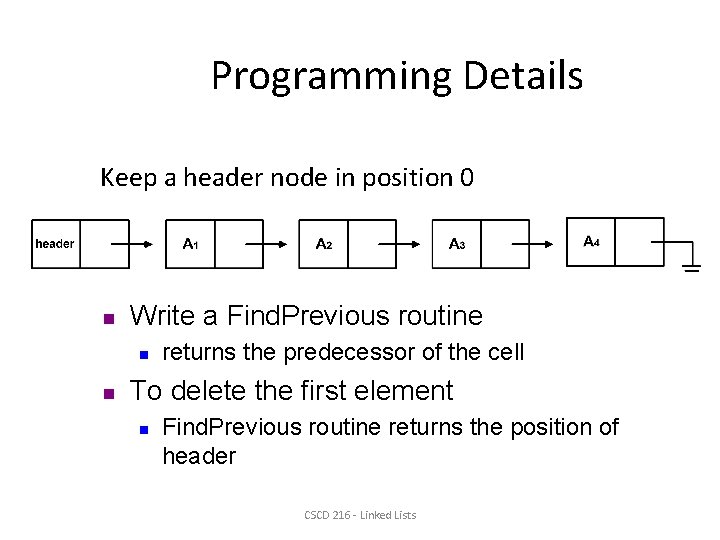
Programming Details • There are 3 special cases for linked lists – Insert an element at the front of the list • there is no really obvious way – Delete an element from the front of the list • changes the start of the list – Delete an element in general • requires to keep track of the node before the deleted one How can we solve these three problems ? CSCD 216 - Linked Lists

Programming Details Keep a header node in position 0 n Write a Find. Previous routine n n returns the predecessor of the cell To delete the first element n Find. Previous routine returns the position of header CSCD 216 - Linked Lists

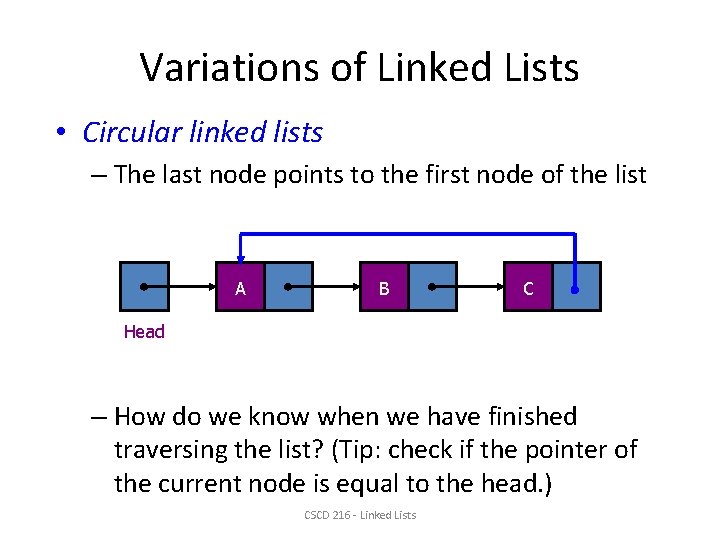
Variations of Linked Lists • Circular linked lists – The last node points to the first node of the list A B C Head – How do we know when we have finished traversing the list? (Tip: check if the pointer of the current node is equal to the head. ) CSCD 216 - Linked Lists

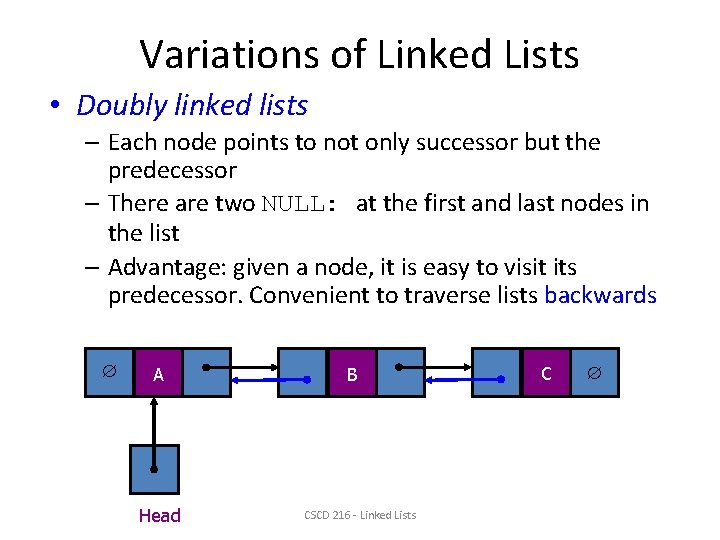
Variations of Linked Lists • Doubly linked lists – Each node points to not only successor but the predecessor – There are two NULL: at the first and last nodes in the list – Advantage: given a node, it is easy to visit its predecessor. Convenient to traverse lists backwards A Head B CSCD 216 - Linked Lists C

Doubly Linked List • Traversing list backwards – not easy with regular lists • Insertion and deletion more pointer fixing • Deletion is easier – Previous node is easy to find CSCD 216 - Linked Lists

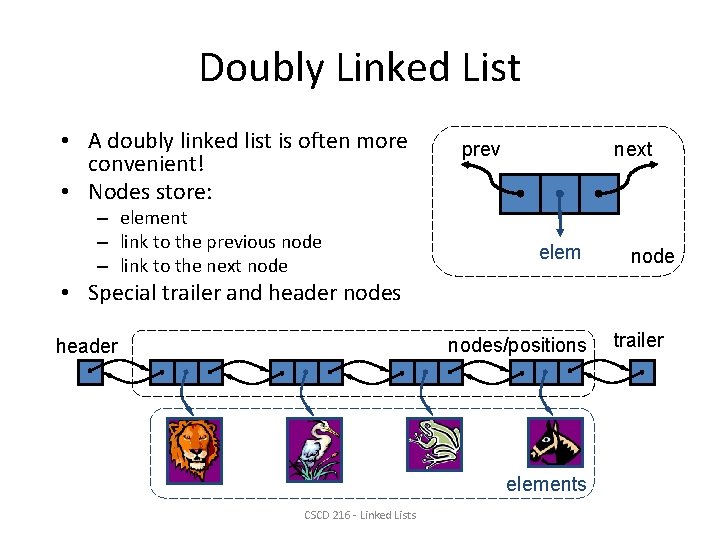
Doubly Linked List • A doubly linked list is often more convenient! • Nodes store: – element – link to the previous node – link to the next node prev next elem node • Special trailer and header nodes/positions header elements CSCD 216 - Linked Lists trailer

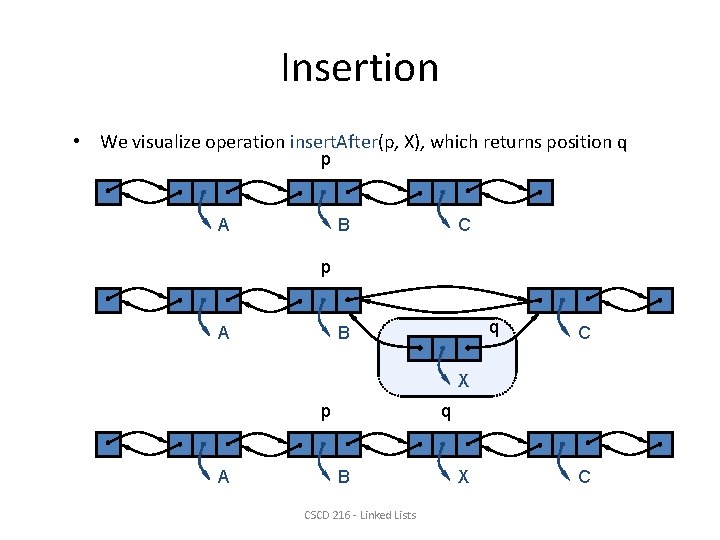
Insertion • We visualize operation insert. After(p, X), which returns position q p A B C p A q B C X p A q B CSCD 216 - Linked Lists X C

Insertion Algorithm insert. After(p, e): Create a new node v link v to its predecessor link v to its successor link p’s old successor to v link p to its new successor, v return v (the position for the element e) CSCD 216 - Linked Lists

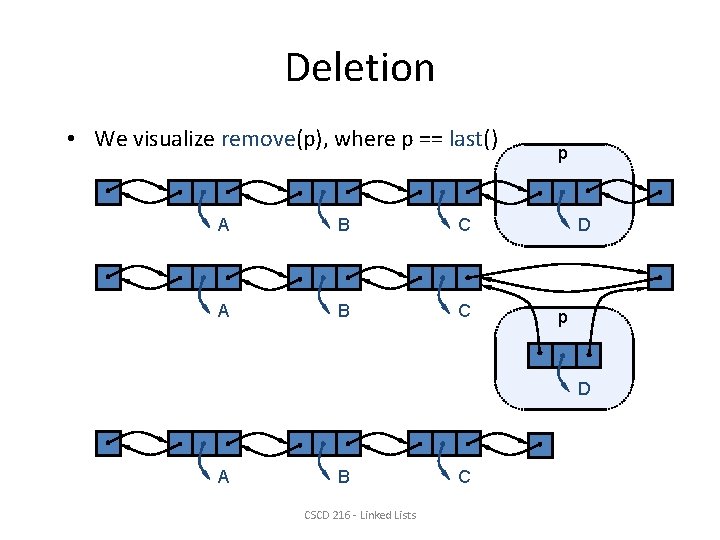
Deletion • We visualize remove(p), where p == last() A B C p D A B CSCD 216 - Linked Lists C

Deletion Algorithm remove(p): CSCD 216 - Linked Lists

Worst-case running time • In a doubly linked list + insertion at head or tail is in O(1) + deletion at either end is on O(1) -- element access is still in O(n) CSCD 216 - Linked Lists

Array versus Linked Lists • Linked lists are more complex to code and manage than arrays, but they have some distinct advantages. – Dynamic: a linked list can easily grow and shrink in size. • We don’t need to know how many nodes will be in the list. They are created in memory as needed. • In contrast, the size of an array is fixed at compilation time. – Easy and fast insertions and deletions • To insert or delete an element in an array, we need to copy to temporary variables to make room for new elements or close the gap caused by deleted elements. • With a linked list, no need to move other nodes. Only need to reset some pointers. CSCD 216 - Linked Lists