SISTEM PERSAMAAN LINIER Matematika2 Sistem Persamaan Linier Homogen

SISTEM PERSAMAAN LINIER Matematika-2

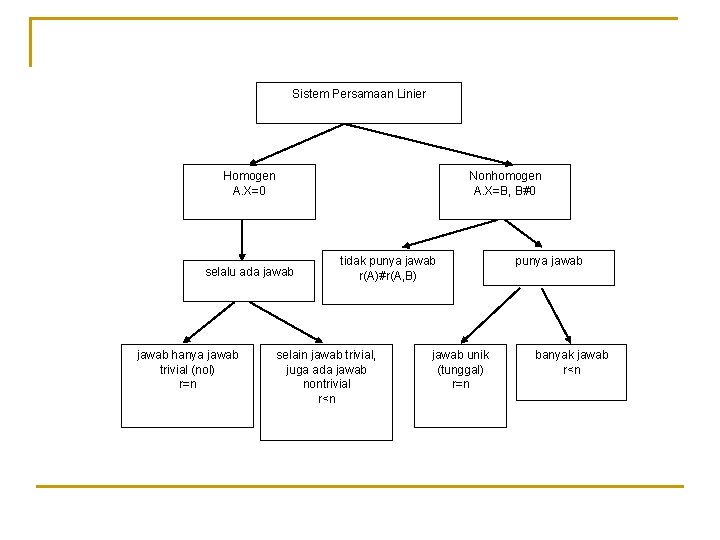
Sistem Persamaan Linier Homogen A. X=0 Nonhomogen A. X=B, B#0 selalu ada jawab hanya jawab trivial (nol) r=n tidak punya jawab r(A)#r(A, B) selain jawab trivial, juga ada jawab nontrivial r<n jawab unik (tunggal) r=n punya jawab banyak jawab r<n

a 11 x 1 + a 12 x 2 + … + a 1 nxn = b 1 a 21 x 1 + a 22 x 2 + … + a 2 nxn = b 2 … … … an 1 x 1 + an 2 x 2 + … + annxn = bn Jika diubah dalam bentuk matriks: A. X = b

X dapat dicari dengan : n X = A-1. b n Cara Cramer n Metode eliminasi Gauss-Jordan n Metode iteratif Jacobi n Metode iteratif Gauss-Seidel

Matriks Invers (A-1) Suatu matriks mempunyai invers jika determinannya # 0. Sifat yang berlaku: n A. A-1 = A-1. A = I n (A-1)-1 = A n (AB)-1 = B-1. A-1

Cara Cramer

Metode Eliminasi Gauss n n n Matriks dari koefisien-koefisien pada sistem persamaan linier dibuat menjadi matriks segitiga atas atau matriks segitiga bawah Jika dibuat matriks segitiga atas, harga x dapat dicari mulai dari xn Jika dibuat matriks segitiga bawah, harga x dapat dicari mulai dari x 1

Metode Eliminasi Gauss-Jordan n n Matriks dari koefisien-koefisien pada sistem persamaan linier dibuat menjadi matriks identitas Harga x 1 sampai xn dapat langsung diketahui

Metode Iteratif Jacobi Misal : a 11 x 1 + a 12 x 2 + a 13 x 3 = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 = b 2 a 31 x 1 + a 32 x 2 + a 33 x 3 = b 3 atau : x 1 = (b 1 – a 12 x 2 –a 13 x 3) / a 11 x 2 = (b 2 – a 21 x 1 – a 23 x 3) / a 22 x 3 = (b 3 – a 31 x 1 – a 32 x 2) / a 33

Penyelesaian n Harga x 1, x 2, dan x 3 awal dihitung dengan memasukkan variabel lainnya = 0 Harga x 1, x 2 dan x 3 tsb. menjadi variabel untuk menghitung harga x 1, x 2, dan x 3 berikutnya Iterasi perhitungan berakhir setelah x 1 n-1 ~ x 1 n; x 2 n-1 ~ x 2 n; x 3 n-1 ~ x 3 n

x 11 = (b 1 – a 12 x 20 –a 13 x 30) / a 11 x 21 = (b 2 – a 21 x 10 – a 23 x 30) / a 22 x 3 1= (b 3 – a 31 x 10 – a 32 x 20) / a 33

Metode Iteratif Gauss-Seidel n n n Harga x 1 awal dihitung dengan memasukkan variabel lainnya = 0 Harga x 2 dihitung dengan harga x 1 baru dan x 3=0 Harga x 3 dihitung dengan harga x 1 dan x 2 baru x 11 = (b 1 – a 12 x 20 –a 13 x 30) / a 11 x 21 = (b 2 – a 21 x 11 – a 23 x 30) / a 22 x 3 1= (b 3 – a 31 x 11 – a 32 x 21) / a 33