Regresi Linear Sederhana dan Korelasi Analisis Regresi Linear

Regresi Linear Sederhana dan Korelasi

Analisis Regresi Linear Sederhana Kegunaan: Model Regression dapat digunakan untuk memprediksi nilai variabel dependen yang dinyatakan sebagai fungsi dari variabel independen setelah model lolos dari analisis. variabel dependen: dinyatakan dengan Y variabel independen : dinyatakan dengan X 1, X 2, …, Xk Jika hanya menggunakan satu variabel independen , model regresi disebut regresi linear sederhana Data sampel digunakan untuk menduga β 0 dan β 1.

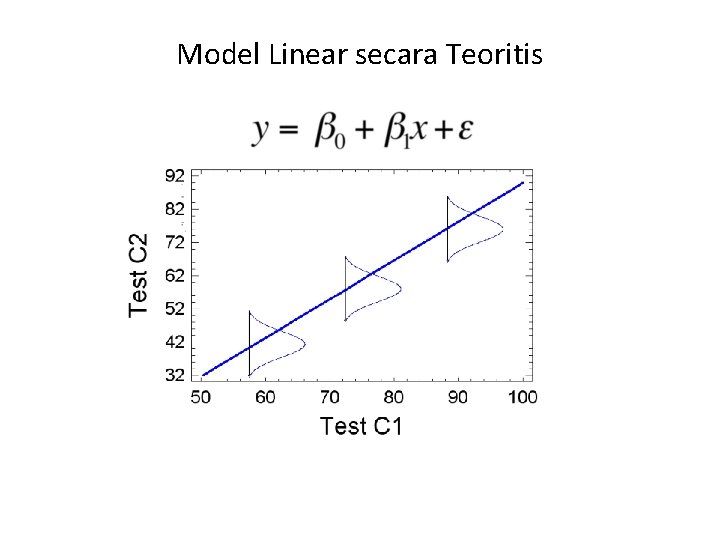
Model Regresi Linear Sederhana variabel : X = variabel independen (dapat ditentukan dari awal) Y = variabel dependen(didapat berdasarkan observasi) Parameters: β 0 = titik potong sumbu Y β 1 = slop/ kemiringan galat ε ~ variabel acak bersebaran normal (με = 0, σε = konstan)

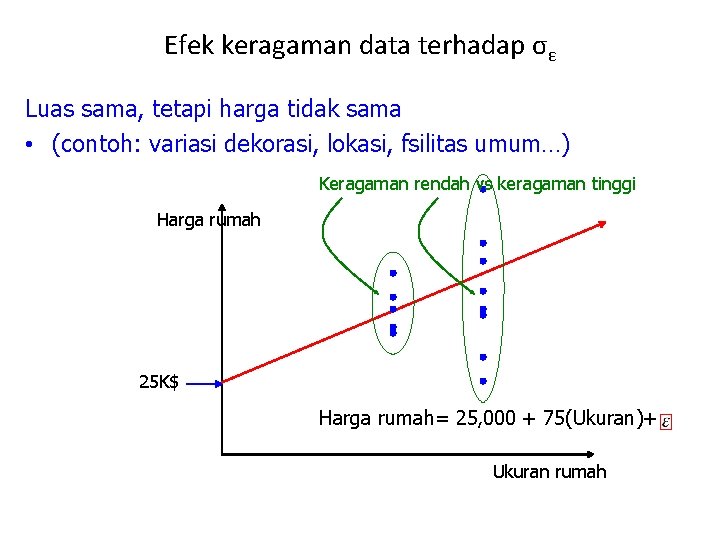
Efek keragaman data terhadap σε Luas sama, tetapi harga tidak sama • (contoh: variasi dekorasi, lokasi, fsilitas umum…) Keragaman rendah vs keragaman tinggi Harga rumah 25 K$ Harga rumah= 25, 000 + 75(Ukuran)+ Ukuran rumah

Model Linear secara Teoritis

Tahapan Analisis Regresi– Pengumpulan Data Ranking Test 2 = β 0 + β 1*(Ranking Test 1) Dari data diduga nilai parameter: β 0 β 1 σε

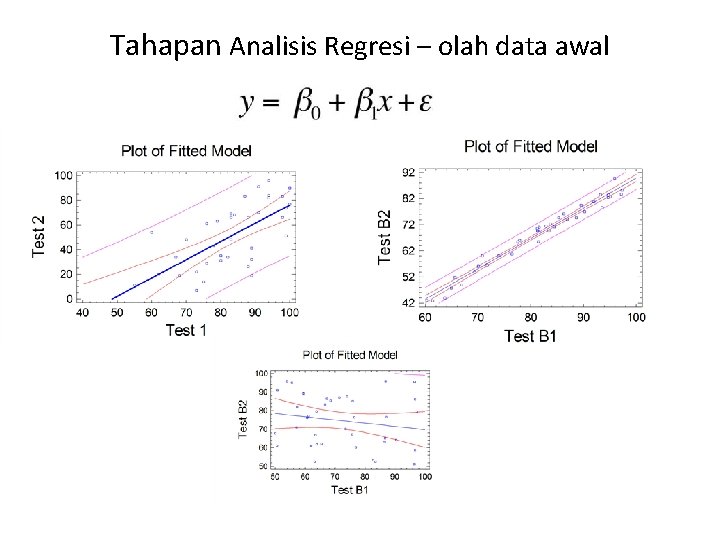
Tahapan Analisis Regresi – olah data awal

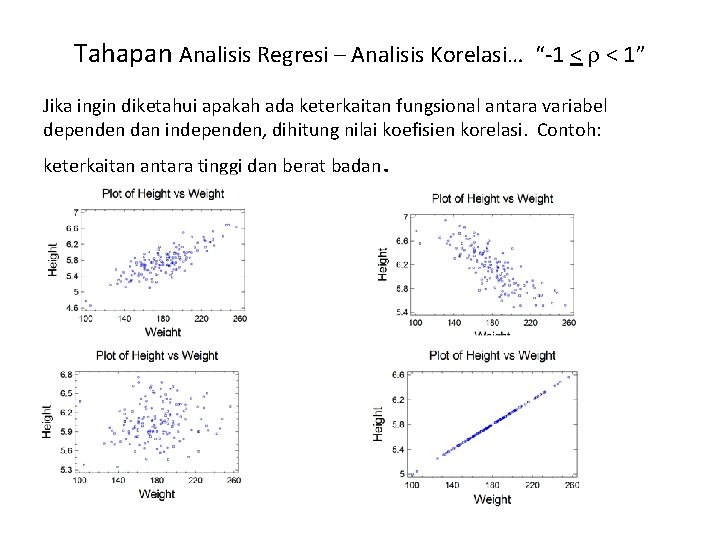
Tahapan Analisis Regresi – Analisis Korelasi… “-1 < < 1” Jika ingin diketahui apakah ada keterkaitan fungsional antara variabel dependen dan independen, dihitung nilai koefisien korelasi. Contoh: keterkaitan antara tinggi dan berat badan .

Tahapan Analisis Regresi – Analisis Korelasi… Jika koefisien korelasi mendekati +1 berarti terdapat keterkaitan antara dua variabel secara searah. Jika koefisien korelasi mendekati -1 berarti terdapat keterkaitan antara dua variabel secara berlawanan arah. Jika koefisien korelasi mendekati 0 berarti tidak terdapat keterkaitan antara dua variabel. Untuk menilai apakah korelasi antar variabel signifikan dapat digunakan pengujian hipothesis.

Model Deterministik Nilai variabel dependen hanya dikaitkan dengan nilai variabel independen dalam bentuk sebuah persamaan linear y = 25, 000 + (75/m 2)(x) Model Probabilistik : Nilai variabel dependen dikaitkan dengan nilai variabel independen dan suatu variabel acak dalam bentuk sebuah persamaan linear –Variabel acak mengakomodasi fenomena realitas data. y = 25, 000 + 75 x + ε Contoh: Tidak semua rumah dengan luasan sama dijual dengan harga sama

Model Regresi Linear Sederhana… Arti dari dan > 0 [kemiringan positif] < 0 [kemiringan negatif] y tegak datar = slope (=tegak/datar) =titik potong garis regresi thd y x

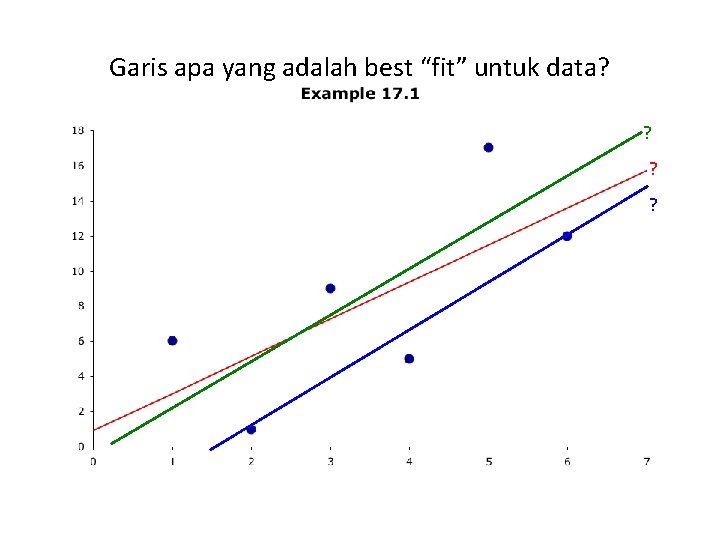
Garis apa yang adalah best “fit” untuk data? ?

Estimasi Koefisien Regresi… Sama halnya dengan sebelumnya, nilai tengah populasi diduga menggunakan rerata sampel. Intersep diduga oleh b 0 dan dengan b 1 least squares garis regresi diberikan oleh: Metode least squares menghasilkan garis lurus yang meminimalkan jumlah kuadrat beda antara data y dan nilai y hat)

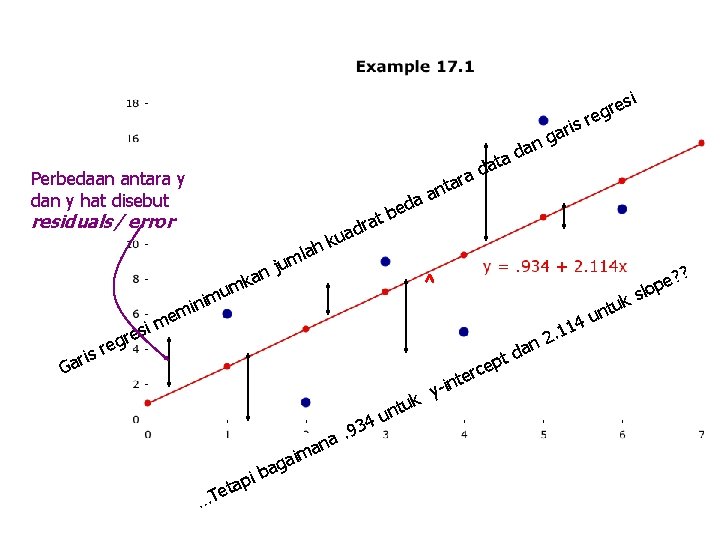
Least Squares Regresi… si Perbedaan antara y dan y hat disebut at d ara nt residuals/ error an k m la m u j h rat d a ku aa d e b an d a is r a g u im min e G aris im s e r reg ep rc inte n yk tu n u 4 3 a. 9 a ma i a g e …T ib p a t re g e r an d t 14 1. 2 uk t n u ? s ? e p lo

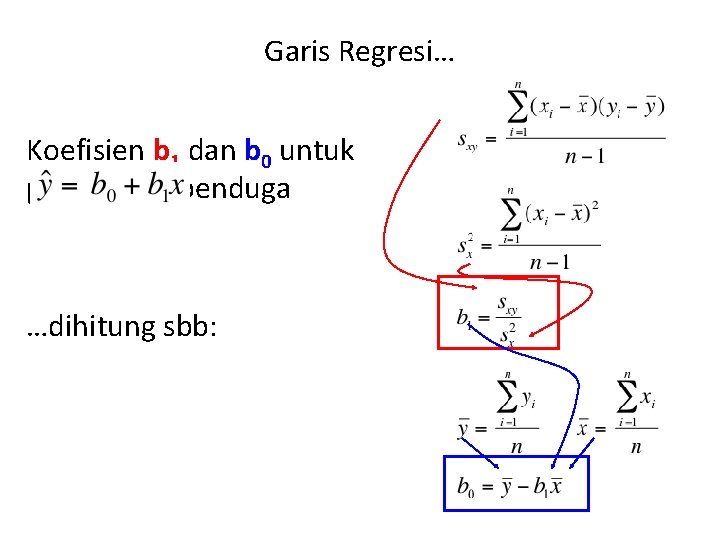
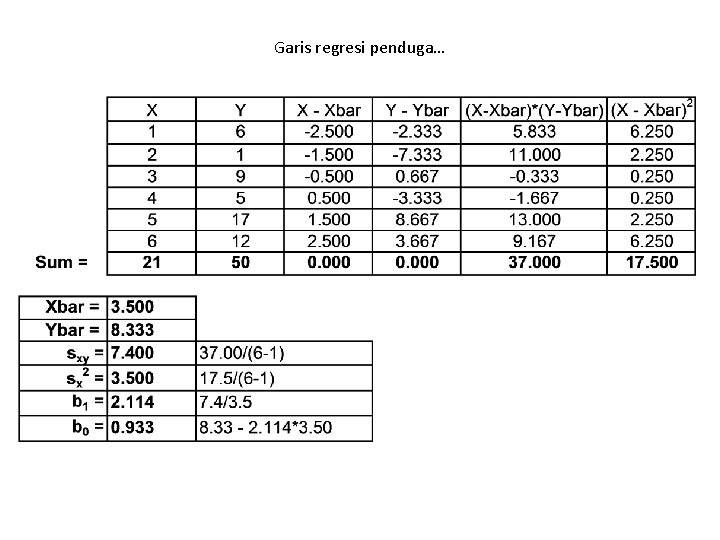
Garis Regresi… Koefisien b 1 dan b 0 untuk persamaan penduga …dihitung sbb:

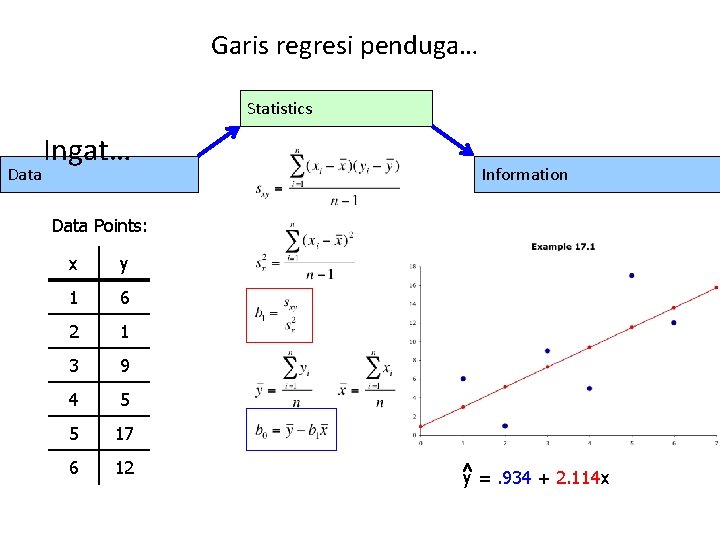
Garis regresi penduga… Statistics Data Ingat… Information Data Points: x y 1 6 2 1 3 9 4 5 5 17 6 12 y =. 934 + 2. 114 x

Garis regresi penduga…

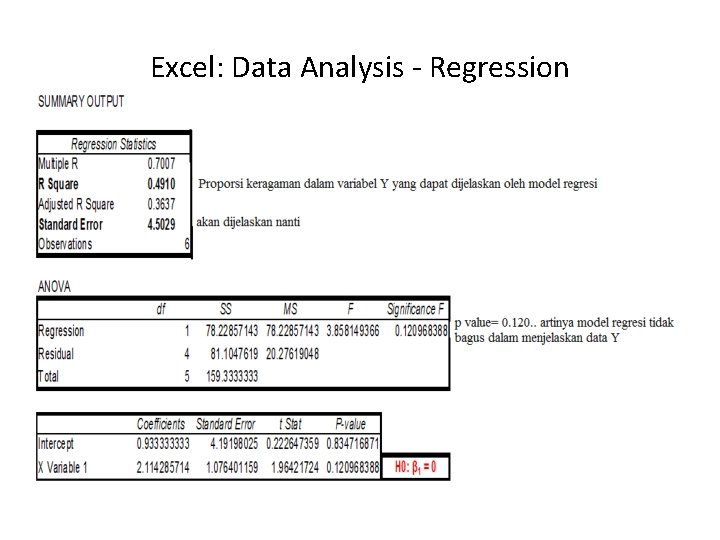
Excel: Data Analysis - Regression

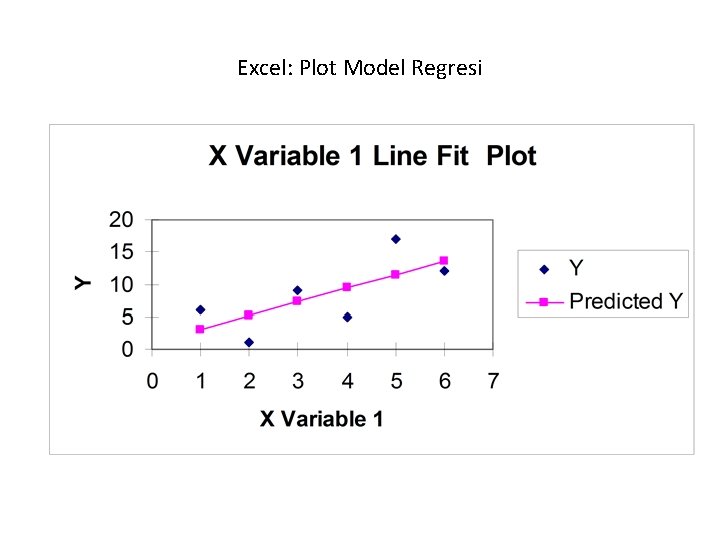
Excel: Plot Model Regresi

Kondisi validitas model regresi… Model regresi akan valid jika empat kondisi dipenuhi: • Sebaran peluang residual normal. • Mean sebaran residual 0. • Simpangan baku residual konstan terhadap nilai variabel independen • Residual independen terhadap nilai variabel dependen y

Menilai model Regresi… Metode least squares akan selalu menghasilkan persamaan garis lurus, sekalipun tidak ada korelasi antara dua macam variabel atau relasi antar variabelnya nonlinear. Sehingga hasil estimasi garis regresi memerlukan penilaian, untuk mengetahui seberapa baik model menjelaskan data. Penilaian menggunakan jumlah kuadrat Error (SSE).

Jumlah Kuadrat Galat (SSE)… SSE dapat dihitung dengan rumus: Digunakan untuk penghitungan simpangan baku garis regresi: Jika nol, semua data menempel pada garis regresi.

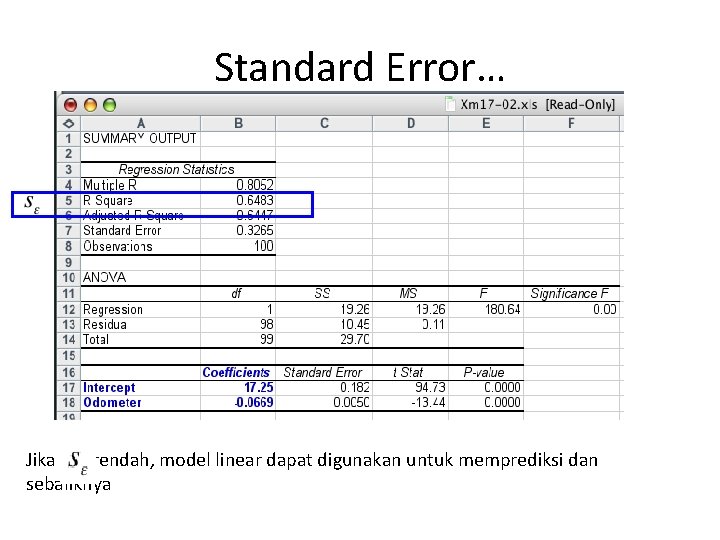
Standard Error… Jika rendah, model linear dapat digunakan untuk memprediksi dan sebaliknya

Standard Error… Pada contoh ini, standard error =. 3265 dan y = 14. 841 Sehingga model regresi linear dari harga mobil sebagai fungsi dari penunjuk nilai pada odometer cukup baik.

Uji untuk Slope…. Jika tidak ada hubungan linear diantara variabel y dan x, maka garis regresi nampak sebagai garis horizontal atau nilai slope = 0. Sebalikanya jika ada hubungan linear diantara variabel y dan x, maka slope ( ) tidak sama dengan 0. Sehingga dapat digunakan uji hipotesis : H 0 : = 0 H 1 : ≠ 0

Uji untuk Slope… Statistik uji untuk pengujian koefisien regresi: H 0: β 1 = 0 Dengan adalah deviasi standard dari b 1: Jika residual ( ) tersebar secara normal, Statistik uji mengikuti sebaran Student t dengan derajat bebas n– 2. Prosedur uji hipotesis 2 arah lebih sering digunakan.

Contoh … Gunakan uji hipotesis statistika untuk menentukan apakah nilai slope berbeda nyata dari 0 pada level signifikan 5%. Uji hipotesis: H 0 : = 0 H 1 : ≠ 0 (Dengan kata lain jika hipotesis nol diterima maka tidak ada bukti bahwa terdapat hubungan linear Daerah penolakan H 0 Atau lihat “p-value” pada output program.

Contoh … Perhatikan output Excel … p-value Nampak statistik t untuk bandingkan “odometer” (slope, b 1) adalah – 13. 49 Lebih rendah dari nilai kritis t. Critical = – 1. 984. Terlihat p-value = 0. 000. Terdapat bukti adanya keterkaitan secara linear antara variabel dependen (harga mobil) dan independen (nilai odometer

Uji untuk Slope… Pendugaan interval dengan tingkat keyakinan tertentu untuk parameter slope , menggunakan konsep IK yang sama. Prakiraan titik untuk menggunakan data sampel adalah b 1. IK (1 -alfa) adalah: Sehingga: Interval ini menduga slope berada dalam selang: –. 0768 dan –. 0570

Koefisien Determinasi… Ukuran seberapa kuat keterkaitan secara linear antara variabel dependen dan independen dihitung dengan koefisien determinasi R 2. Koefisien Determinasi = kuadrat dari koefisien korelasi (r), atau R 2 = (r)2

Koefisien Determinasi Jika R 2 =. 6483, Berarti model regresi yang digunakan dapat menjelaskan 64. 83% total keragaman harga jual rumah (y). Sedangkan 35. 17% merupakan keragaman yang tidak dapat dijelaskan oleh model (error) Koefisien Determinasi tidak mempunyai nilai kritis, sehingga tidak dapat dilakukan uji hipotesis nilai statistiknya. Secara umum makin besar R 2, semakin baik kesesuaian model dengan data. R 2 = 1: Data menempel pada garis regresi. R 2 = 0: tidak ada hubungan linear antara x dan y.

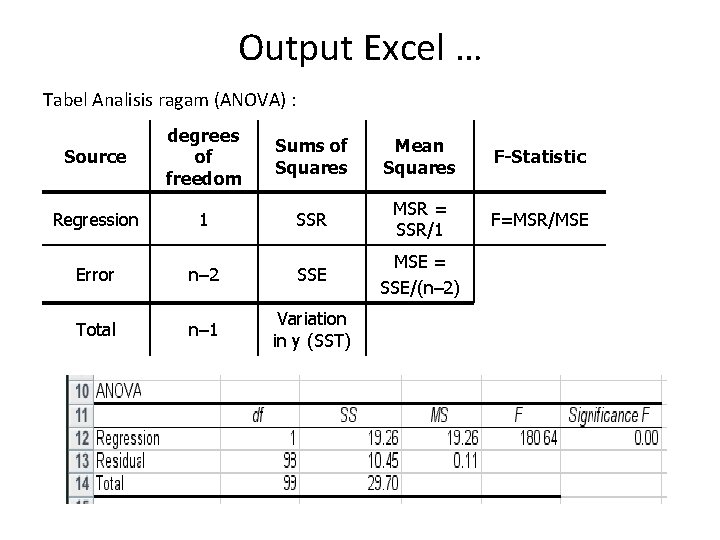
Output Excel … Tabel Analisis ragam (ANOVA) : Source degrees of freedom Sums of Squares Mean Squares F-Statistic Regression 1 SSR MSR = SSR/1 F=MSR/MSE Error n– 2 SSE MSE = SSE/(n– 2) Total n– 1 Variation in y (SST)

Penggunaan Persamaan Regresi… Persamaan regresi : y = 17. 250 –. 0669 x Dapat digunakan untuk predikasi harga jual mobil dengan odometer 40 (40, 000) km: y = 17. 250 –. 0669 x = 17. 250 –. 0669(40) = 14, 574 Nilai ($14, 574) adalah estimasi titik. Interval konfidensi dapat digunakan untuk predikasi tersebut karena harga jual sering berbeda untuk kondisi sama.

Interval Predikasi Interval predikasi digunakan jika diinginkan untuk memprediksi suatu nilai dari variabel dependen, berdasarkan suatu nilai variabel independen (xg = nilai variabel independen x di mana nilai variabel dependen y ingin diramalkan)

Pendugaan Interval Konfidensi untuk Nilai Tengah Y… Penduga interval konfidensi untuk nilai tengah y (Mean dari Y) digunakan jika diinginkan prakiraan sebuah selang dalam tingkat keyakinan (1 - alfa) di mana garis regresi terdapat di dalamnya. Estimasi mean y, untuk suatu nilai x adalah: (Secara teory, formula di atas digunakan untuk jumlah data populasi tak hingga. Namun dari hasil ini dapat diintepretasikan, sebagai harga jual rerato mobil tipe “XXX” dengan odometer menunjuk nilai 40, 000

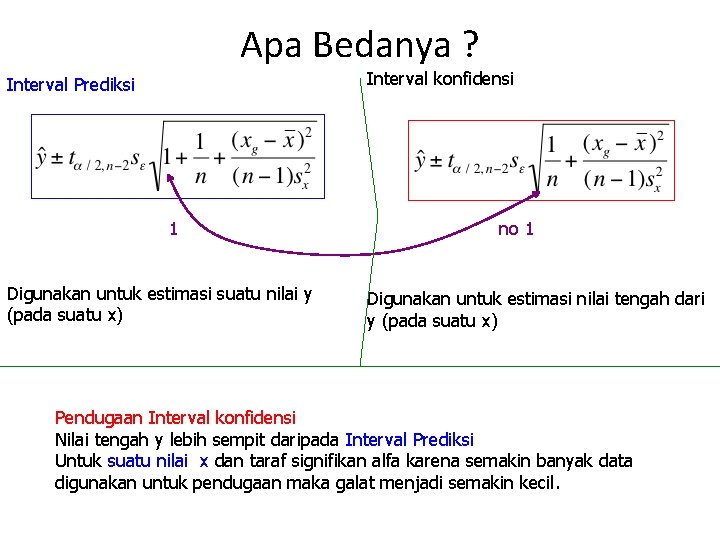
Apa Bedanya ? Interval konfidensi Interval Prediksi 1 Digunakan untuk estimasi suatu nilai y (pada suatu x) no 1 Digunakan untuk estimasi nilai tengah dari y (pada suatu x) Pendugaan Interval konfidensi Nilai tengah y lebih sempit daripada Interval Prediksi Untuk suatu nilai x dan taraf signifikan alfa karena semakin banyak data digunakan untuk pendugaan maka galat menjadi semakin kecil.

Penilaian Model Regresi… Tiga hal dalam melakukan analisis model regresi: • Variabel error harus menyebar normal, • ragam Variabel error harus konstan, • Variabel error harus saling bebas. Untuk memeriksa apakah tiga kondisi terpenuhi dilakukan Analysis Residual, untuk melihat apakah sebaran variabel acak residual memenuhi ketiga kriteria tersebut

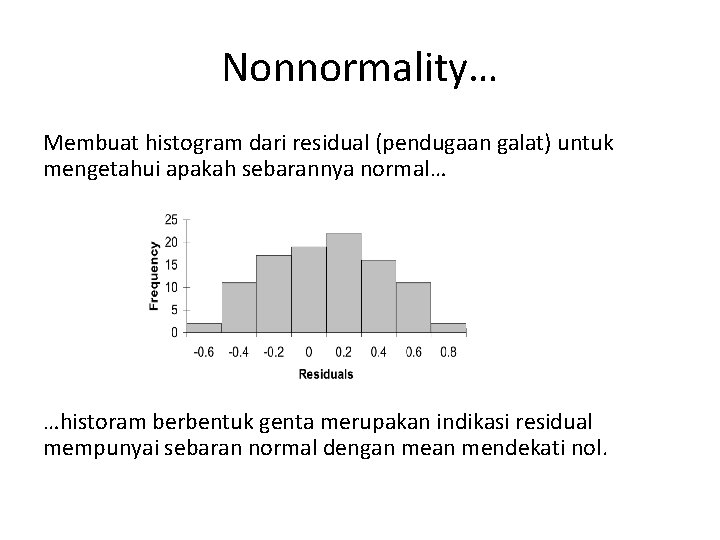
Nonnormality… Membuat histogram dari residual (pendugaan galat) untuk mengetahui apakah sebarannya normal… …historam berbentuk genta merupakan indikasi residual mempunyai sebaran normal dengan mendekati nol.

Heteroskedastisitas… Jika asumsi keragaman residual yang konstan tidak dipenuhi, hal ini disebut heteroskedastisitas. Heteroskedastisitas dapat terjadi jika plot antara residual dan nilai prediksi y-hat yang semakin melebar seiring bertambahnya nilai y-hat pada sumbu datar.

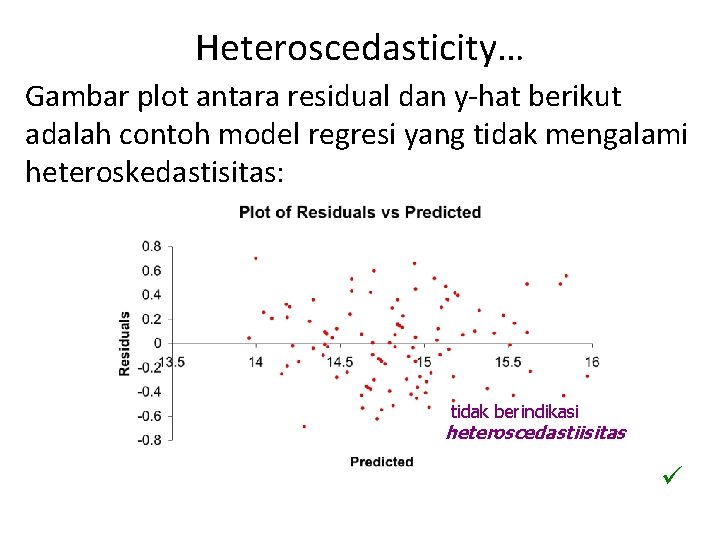
Heteroscedasticity… Gambar plot antara residual dan y-hat berikut adalah contoh model regresi yang tidak mengalami heteroskedastisitas: tidak berindikasi heteroscedastiisitas

Otokorelasi Residual Jika data residual diurutkan menurut waktu maka akan diperoleh data time series. Untuk data time series, sering dijumpai error saling berkorelasi, disebut autocorrelated atau serially correlated. Deteksi autocorrelation dengan membuat grafik nilai residuals terhadap waktu. Pola beraturan (trend, siklus) mengindikasi asumsi otokorelasi dilanggar.

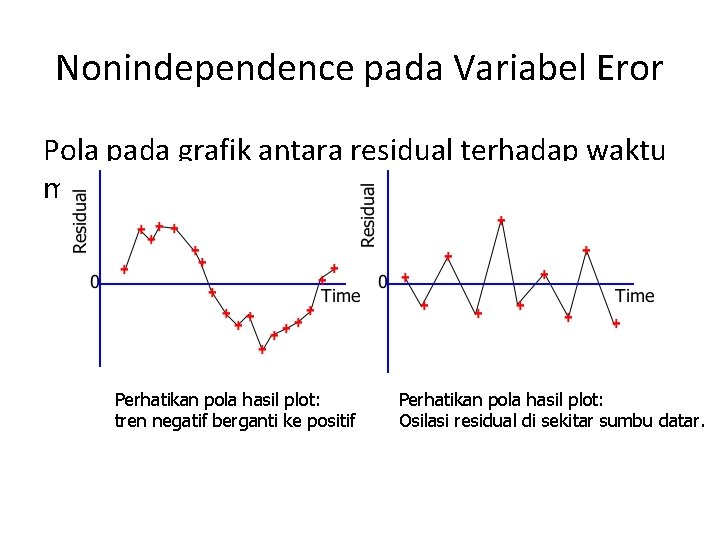
Nonindependence pada Variabel Eror Pola pada grafik antara residual terhadap waktu menunjukkan adanya otokorelasi Perhatikan pola hasil plot: tren negatif berganti ke positif Perhatikan pola hasil plot: Osilasi residual di sekitar sumbu datar.

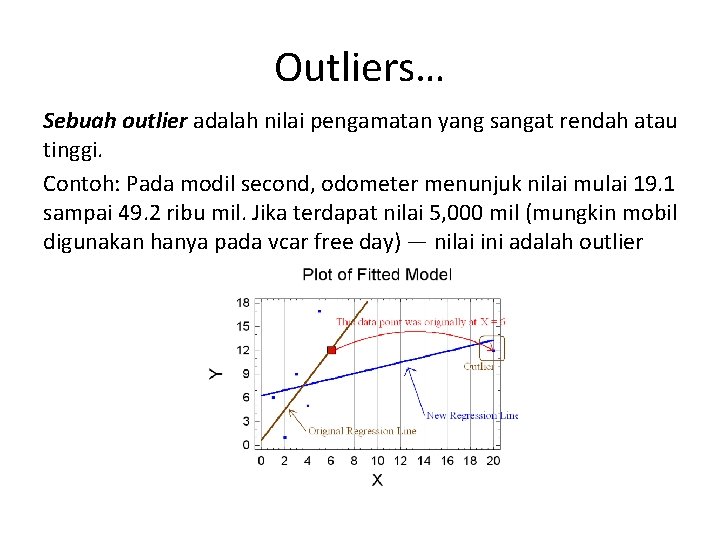
Outliers… Sebuah outlier adalah nilai pengamatan yang sangat rendah atau tinggi. Contoh: Pada modil second, odometer menunjuk nilai mulai 19. 1 sampai 49. 2 ribu mil. Jika terdapat nilai 5, 000 mil (mungkin mobil digunakan hanya pada vcar free day) — nilai ini adalah outlier

Outliers… Data Outlier terjadi karena: • Kesalahan dalam input data (operator keliru) • Data seharusnya bukan elemen populasi sehingga tidak dapat digunakan sebagai sampel * Mungkin memang data valid. Outliers dapat dideteksi menggunakan scatter plot. Outlier memerlukan penanganan khusus karena kalau tidak sangat memengaruhi hasil estimasi regresi

Prosedur untuk mementukan Model Regresi… 1. 2. 3. 4. 5. 6. 7. Pengembangan Model yang didukung teori. Pengumpulan data untuk mendapat sampel dua macam variabel. Membuat diagram pencar untuk melihat apakah model linear sesuai untuk data tersebut. Tandai apakah terdapat pengamatan terpencar jauh (outliers). Estimasi parameter model regresi. Hitung residual (selisish antara data y dan y-hat) dan periksa apakah empat kondisi residual dipenuhi Uji signifikansi parameter model, dan kemampuan model dalam menjelaskan keragaman data variabel tidak bebas Jika model lulus uji pada langkah (6) maka persamaan regresi dapat digunakan untuk melakukan prediksi.

Cara menggunakan Excel untuk Regresi Sederhana • Pada instalasi excel yang dikerjakan secara lengkap, Untuk dapat menggunakan fungsi regresi secara cepat/otomatis dapat digunakan menu adds-ins dengan meng-klik simbol windows pada windows 7, yaitu dengan meng-klik “excel options” dan kemudian memilih opsi “add-ins” dan tekan tombol “go” pada opsi “excel add-ins. Kemudian pilih “tool-pak” pada menu tersebut. • Jika instalasi excel tidak lengkap, maka hanya dapat dilakukan secara manual menggunakan fungsi “Statistical” pada menu “formulas” untuk opsi “more functions”

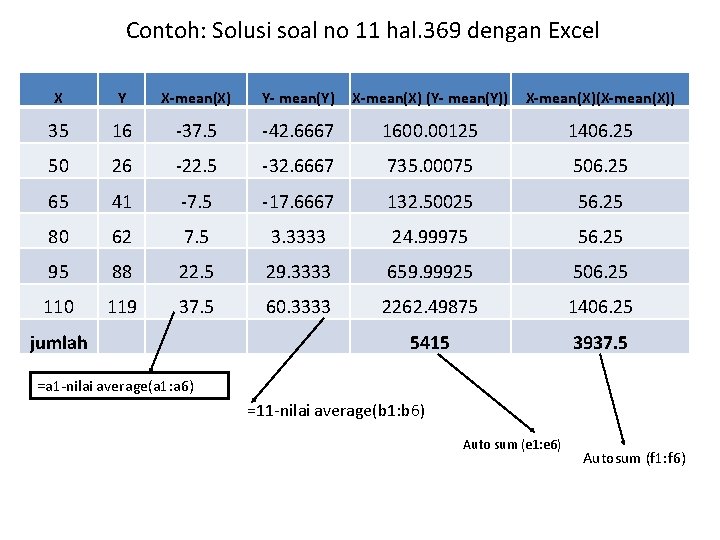
Contoh: Solusi soal no 11 hal. 369 dengan Excel X Y X-mean(X) Y- mean(Y) X-mean(X) (Y- mean(Y)) X-mean(X)(X-mean(X)) 35 16 -37. 5 -42. 6667 1600. 00125 1406. 25 50 26 -22. 5 -32. 6667 735. 00075 506. 25 65 41 -7. 5 -17. 6667 132. 50025 56. 25 80 62 7. 5 3. 3333 24. 99975 56. 25 95 88 22. 5 29. 3333 659. 99925 506. 25 110 119 37. 5 60. 3333 2262. 49875 1406. 25 5415 3937. 5 jumlah =a 1 -nilai average(a 1: a 6) =11 -nilai average(b 1: b 6) Auto sum (e 1: e 6) Autosum (f 1: f 6)

mean(X) Mean(Y) Sxy Sx 2 b a Rsqr Std Error Lanjutan solusi dg. excel 72. 5 58. 66666667 1083 787. 5 1. 375238095 -41. 03809524 0. 965710334 Gunakan formula slope atau fungsi ‘slope’ Gunakan formula intersep atau fungsi ‘intercept’ 98. 1705028 Std Error = sqr(SSE/n-2) dengan SSE=(n-1)*((Y-mean(Y))*(Y-mean(Y)) - slope(b 1: b 6; a 1: a 6))