Simulationsound NIZK Proofs for a Practical Language and

Simulation-sound NIZK Proofs for a Practical Language and Constant Size Group Signatures Jens Groth University of California Los Angeles Presenter: Eike Kiltz, CWI

Overview Group signatures Simulation-extractable NIZK for PPEs Digital signatures RCCA-secure encryption NIZK proofs for Pairing Product Equations Groups with bilinear map

Bilinear groups G, GT cyclic groups of prime order p g generator for G Bilinear map e: G G GT e(ga, gb) = e(g, g)ab e(g, g) generator for GT

El. Gamal encryption fails Public key: g, h Encrypt message m: (u, v) = (gr, hrm) Not semantically secure, can for instance tell whether ciphertext (u, v) contains 1: e(u, h) = e(gr, h) = e(g, h)r= e(g, hr) e(g, v) = e(g, hrm)

BBS-encryption [BBS 04] Public key: f, h, g Secret key: x, y so f = gx, h= gy Encrypt message m: (u, v, w) = (fr, hs, gr+sm) Decrypt (u, v, w): m = w u-1/x v-1/y

Security assumption Decisional linear assumption [BBS 04]: f, h, g, fr, hs, gt Hard to distinguish tuples with t = r+s from tuples with t random Generalization of DDH (s = 0)

Example: verifiable encryption Public key: f, h, g Encryption of message m: (u, v, w) = (fr, hs, gr+sm) Statement ”m is plaintext of (u, v, w)”: e(u, h) = e(f, x) e(wm-1, h) = e(g, xv) Witness for satisfiability: x = hr

Pairing product equations Equation over variables x 1, . . . , xn eki fki ke(ak ixi , bk ixi ) = 1 for constants ak, bk G , eki, fki Zp Length of pairing product equation: k=1, . . . , l Earlier example, equation over x: e(u, h) = e(f, x) ↔ e(ux 0, hx 0)e(fx 0, x-1) = 1

Satisfiability of pairing product equations Given a set of pairing product equations S = {eq 1, . . . , eqm} over variables x 1, . . . , xn Satisfiability of pairing product equations: Does there exist a choice of x 1, . . . , xn G so all m equations are satisfied?

Satisfiability of pairing product equations • Relations between group elements • Direct expression, no reduction to Circuit SAT ! • At the same time very general: From S 1, . . . , SL can construct SAND: All Si simultaneously satisfiable SOR: Exists Si that is satisfiable NP-complete

NIZK Proofs Common reference string: crs Statement: S satisfiable Witness x 1, . . . xn Prover Soundness: NP-language valid proof →S satisfiable Zeroknowledge: S satisfiable, but I learned Verifier nothing else

NIZK proof for satisfiability of pairing product equations n n Perfect completeness, perfect soundness and computational zero-knowledge Common reference string: 6 group elements NIZK proof for set S = {eq 1, . . . , eqm} with total length L = l 1+. . . +lm over variables x 1, . . . , xn: 4 n + 228 L - 3 m group elements In other words: O(1) size crs, O(n+L) size proofs

Main technical contribution NIZK proof for a practical language: Satisfiability of pairing product equations Consequences: Efficient simulation-extractable NIZK proofs Group signatures with constant

Overview Group signatures Simulation-extractable NIZK for PPEs Digital signatures RCCA-secure encryption NIZK proofs for Pairing Product Equations Groups with bilinear map

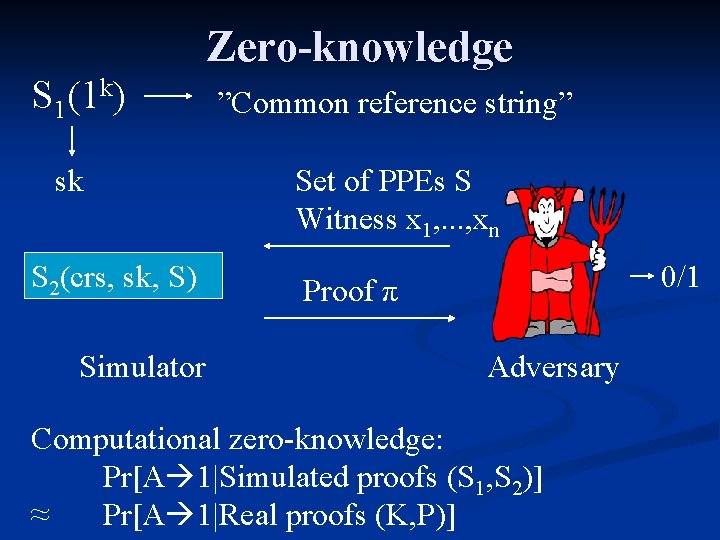
Zero-knowledge S 1(1 k) ”Common reference string” sk Set of PPEs S Witness x 1, . . . , xn S 2(crs, sk, S) Simulator 0/1 Proof π Adversary Computational zero-knowledge: Pr[A 1|Simulated proofs (S 1, S 2)] ≈ Pr[A 1|Real proofs (K, P)]

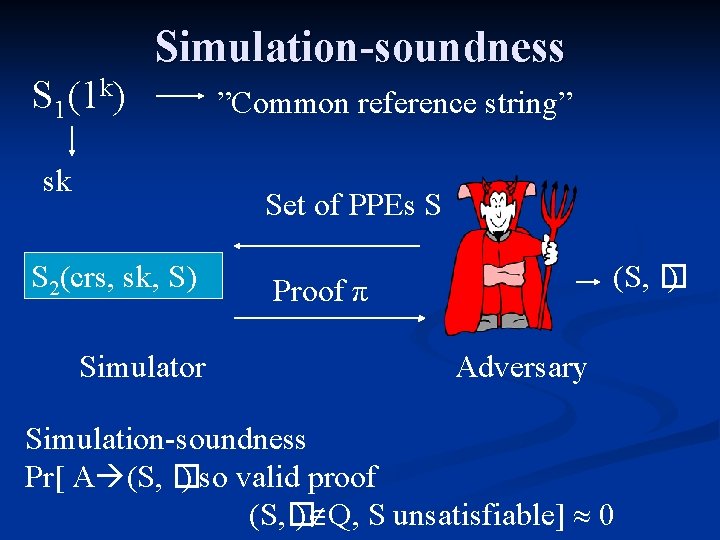
Simulation-soundness S 1(1 k) sk ”Common reference string” Set of PPEs S S 2(crs, sk, S) Simulator (S, � ) Proof π Adversary Simulation-soundness Pr[ A (S, � ) so valid proof (S, � ) Q, S unsatisfiable] 0

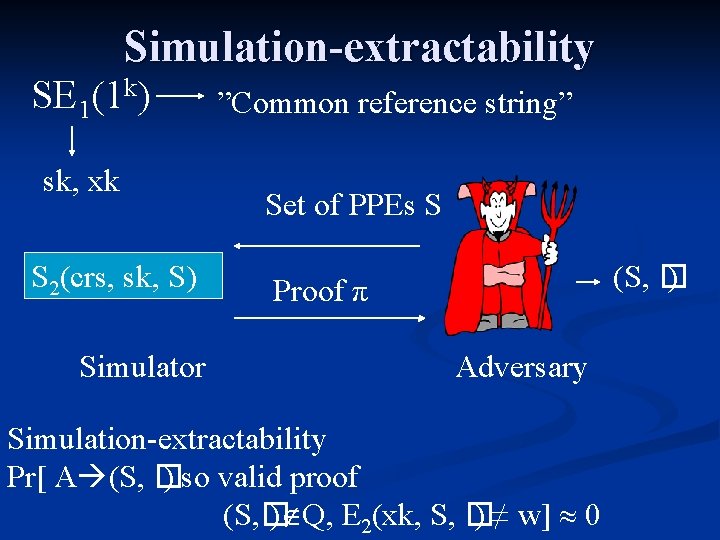
Simulation-extractability SE 1(1 k) sk, xk S 2(crs, sk, S) Simulator ”Common reference string” Set of PPEs S (S, � ) Proof π Adversary Simulation-extractability Pr[ A (S, � ) so valid proof (S, � ) Q, E 2(xk, S, � ) ≠ w] 0

Simulation-extractable NIZK n n Simulation-extractable NIZK proof for satisfiability of pairing product equations CRS: O(1) group elements Proofs: O(n+L) group elements Comparison for Circuit SAT: Our proof size: O(|C|k) bits Previous: O(|C|k + poly(k)) bits

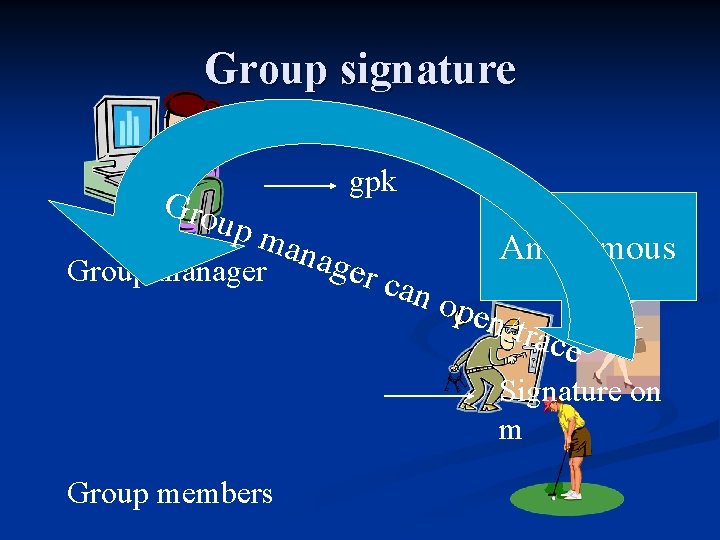
Group signature gpk Gro up m anag Anonymous er c Group manager an o pen/ trac e Signature on m Group members

Group signature Group public key: vkcert, pkcpa, crs Group manager’s join key: skcert Group manager’s open key: dkcpa Join user i: User: keys GM: (vki, ski) ← CMA-secure signature certi ← signskcert(vki) User i’s public key: vki, certi

Group signature Group public key: vkcert, pkcpa, crs Group signature by member i on message m: keys (vksots, sksots) ← strong one-time signature c ← Epk (vki, certi, signsk (vksots)) cpa i �← Simulation-extractable NIZK proof for ”c has certified vki and signature on vksots” sig ← signsksots(m, vksots, c, � )

Group signature n n n Key sizes: O(1) group elements Group signature: O(1) group elements (huge) Strong security: [BMW 03, BSZ 05] Dynamic group: join members Full-anonymity: anonymous under adaptive opening attack Full-traceability: GM can track user, no framing Assumption: decisional linear assumption Compare with BSZ 05: general construction, poly-size proofs BW 06: O(log n) group elements, static group, CPA-security ACHd. M 05: O(1) group elements, key exposure

Thanks Acknowledgment: Rafail Ostrovsky, Amit Sahai and Brent Waters for helpful discussions and comments I do apologize for not being here myself today. Questions can be sent to jg@cs. ucla. edu Thanks a lot to Eike for presenting!