New Techniques for NIZK Jens Groth Rafail Ostrovsky

New Techniques for NIZK Jens Groth Rafail Ostrovsky Amit Sahai University of California Los Angeles

Motivation OK, I will make a zero I’m a-knowledge woman. proof Prove it! Circuit C = ”I’m a woman” Proof π

Completeness Common reference string K(1 k) Circuit C Witness w so C(w)=1 Proof π Accept Prover Verifier Perfect completeness: Pr[Accept] = 1

Soundness Common reference string K(1 k) Unsatisfiable C Proof π Adversary Reject Verifier Perfect soundness: Pr[Reject] = 1

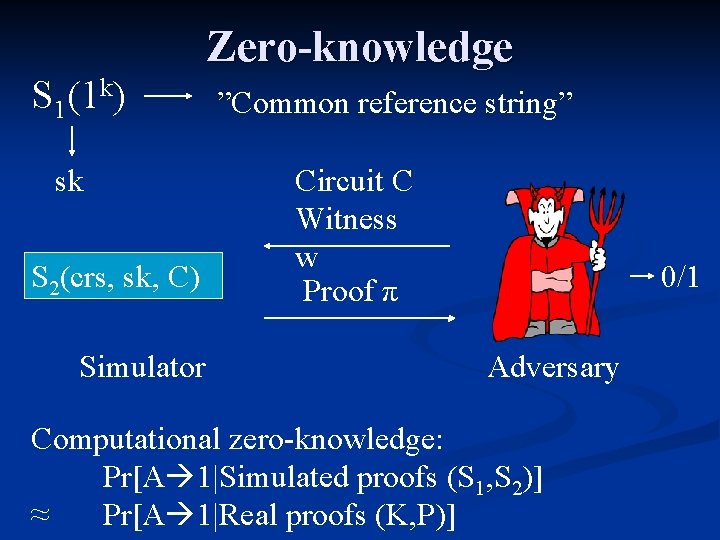
Zero-knowledge S 1(1 k) sk S 2(crs, sk, C) Simulator ”Common reference string” Circuit C Witness w Proof π 0/1 Adversary Computational zero-knowledge: Pr[A 1|Simulated proofs (S 1, S 2)] ≈ Pr[A 1|Real proofs (K, P)]

NIZK proof for Circuit SAT 1 NAND Circuit SAT is NP complete w 4 NAND w 1 w 2 w 3

Homomorphic proof commitment Two types of indistinguishable public keys: n Perfect trapdoor (pk, tk) ← Khiding(1 k) n Perfect binding pk ← Kbinding(1 k) Homomorphic Message space size at least 4 (3 also ok) Witness indistinguishable proof that commitment contains 0 or 1 n Perfect soundness on perfect binding key n Perfect WI on perfect trapdoor key

Bilinear group of order n G, GT cyclic groups of order n = pq g generator for G bilinear map e: G G GT e(ua, vb) = e(u, v)ab e(g, g) generates GT Decision subgroup problem ord(h) = q or ord(h) = n ?

BGN-based commitment Perfect binding key: ord(g) = n, ord(h) = q Perfect hiding key: ord(g) = ord(h) = n and g=hx Commitment: Com(m; r) = gmhr Homomorphic: gm+Mhr+R = gmhr g. Mh. R where r Zn

WI proof for commit to 0 or 1 Wish to prove c commitment to 0 or 1 Write c = gmhr (m mod p unique if h order q) e(c, g-1 c) = e(gmhr, gm-1 hr) = e(g, g)m(m-1) e(hr, g 2 m-1 hr) = e(h, (g 2 m-1 hr)r ) = e(h, π) Proof is: π = (g 2 m-1 hr)r Soundness when h has order q: e(g, g)m(m-1) e(hr, g 2 m-1 hr) = e(h, π) so m = 0, 1 mod p Witness indistinguishability when h has order n: Unique π so e(c, g-1 c) = e(h, π)

NIZK proof for Circuit SAT WI proof w 4 = (w 1 w 2) com(1) NAND WI proof 1 = (w 4 w 3) c = com(w ) 4 4 NAND WI proof c 1 commit to 0 or 1 WI proof c 2 commit to 0 or 1 WI proof c 3 commit to 0 or 1 WI proof c 4 commit to 0 or 1 c 1 = com(w 1) c 3 = com(w 3) c 2 = com(w 2)

WI proof for NAND-gate Given c 0, c 1, c 2 commitments containing bits b 0, b 1, b 2 wish to prove b 2 = (b 0 b 1) if and only if b 0 + b 1 + 2 b 2 - 2 {0, 1} WI proof c 0 c 1 c 22 com(-2) commitment to 0 or 1

NIZK proof for Circuit SAT Commit to all wires wi as ci = com(wi) n For each i make WI proof that ci contains 0 or 1 n For each NAND-gate make WI proof that c 0 c 1 c 22 com(-2) contains 0 or 1 n Perfect completeness Perfect binding key - perfect soundness Perfect trapdoor key - perfect zero-knowledge

Perfect NIZK on perfect trapdoor key Simulation: Make trapdoor commitments Trapdoor-open relevant commitments to 0 and WI prove Proof that simulation works on C with w so C(w)=1: Can trapdoor-open commitments to wi’s and WI prove By perfect witness-indistinguishability of the WI proofs indistinguishable from simulation Can from the start make commitments to wi’s By perfect hiding of the commitments indistinguishable from previous method Corresponds to real proof on trapdoor key

First result Use Kbinding to generate pk NIZK proof with perfect completeness perfect soundness computational ZK CRS size: O(k) bits Proof size: O(|C|k) bits Compare with: O(|C|k 2) proofs [KP]

Second result Use Khiding to generate pk NIZK argument with perfect completeness computational co-soundness perfect zero-knowledge CRS size: O(k) bits Proof size: O(|C|k) bits Compare with: None

Adaptive co-soundness common reference string C, wco Proof π Khiding Reject wco witness for C unsatisfiable Computational co-soundness: Pr[Reject] ≈ 1

Third result Protocol: Non-interactive Statistical ZK UC NIZK proof secure against adaptive adversary Compare with: Interactive UC ZK proofs [DN, CLOS] UC NIZK proofs secure against nonadaptive adversary [DDOPS]

Non-interactive zaps for Circuit SAT No common reference string n Perfect completeness: (C, w) so C(w)=1 π ← P(1 k, C, w) : V(1 k, C , π)=1 n Perfect soundness: (C, π) with C unsatisfiable V(1 k, C, π)=0 n Computational witness-indistinguishability: (C, w 0, w 1) so C(w 0)=1 and C(w 1)=1 P(1 k, C, w 0) ≈ P(1 k, C, w 1) n

Naïve idea: Non-interactive zaps Prover chooses public key and makes NIZK proof Problem: Can choose trapdoor key and prove anything Better idea: Prover chooses two public keys and makes an NIZK proof with each of them Makes choice so: One is trapdoor, one is perfect binding Verifiable that at least one key is perfect binding Verifier cannot tell which key is trapdoor

Witness-indistinguishability Circuit C and two witnesses w 0, w 1 • Generate pk 0 perfect trapdoor and pk 1 perfect binding • NIZK proof using w 0 on pk 0 NIZK proof using w 0 on pk 1 • Simulate proof on trapdoor pk 0 NIZK proof using w 0 on pk 1 • NIZK proof using w 1 on pk 0 NIZK proof using w 0 on pk 1 • Switch to pk 0 perfect binding and pk 1 perfect trapdoor • NIZK proof using w 1 on pk 0 Simulate proof on trapdoor pk 1 • NIZK proof using w 1 on pk 0 NIZK proof using w 1 on pk 1 • Switch back to pk 0 perfect trapdoor and pk 1 perfect binding

Fourth result Use verifiable pairs of public keys At least one of two keys is perfect binding The other is trapdoor Indistinguishable which one is trapdoor Non-interactive ZAP Proof size O(|C|k) bits Compare with: 2 -move zaps [DN] Non-interactive zaps [BOV] huge proofs, non-standard assumption

Bilinear groups G, GT cyclic groups of prime order p g generator for G bilinear map e: G G GT e(ga, gb) = e(g, g)ab e(g, g) generator for GT Decisional linear problem [BBS] f, h, g, u = f. R, v = h. S, w = g. T T = R+S or T random ?

Commitment scheme Public key f = gx, h = gy, u = f. R, v = h. S, w = g. T pk = (p, G, GT, e, g, f, h, u, v, w) Commitment to m Zp c = (umfr, vmhs, wmgr+s) Perfect hiding trapdoor if T = R+S = (fm. R+r, hm. S+s, gm(R+S)+r+s)

Commitment scheme Commitment to m Zp c = (umfr, vmhs, wmgr+s) Perfect binding if T ≠ R+S = (c 1, c 2, c 3) because c 3 c 2 -1/xc 1 -1/y = (wu-1/xv-1/y)m = g(T/(R+S))m uniquely defines m

Commitment scheme Commitment to m Zp c = (umfr, vmhs, wmgr+s) Homomorphic (umfr, vmhs, wmgr+s) (u. Mf. R, v. Mh. S, w. Mg. R+S) = (um+Mfr+R, vm+Mhs+S, wm+Mgr+R+s+S) Witness indistinguishable proof of commitment to message 0 or 1 - Perfect sound on perfect binding key - Perfect WI on perfect trapdoor key

Choosing two keys Elliptic curve E: y 2 = x 3 +1 mod q, where q smallest suitable prime so E has order p subgroup. Easy to verify p is prime, p defines (G, GT, e), easy to verify that g is order p point on curve. Choose x, y ← Zp*, R, S ← Zp and set f = gx, h = gy, u = f. R, v = h. S, w = g. R+S Output two public keys (p, G, GT, e, g, f, h, u, v, w) (p, G, GT, e, g, f, h, u, v, wg) At least one must be perfectly binding, but by decisional linear assumption hard to tell which one