Sequential Timing Optimization Long path timing constraints Data

Sequential Timing Optimization

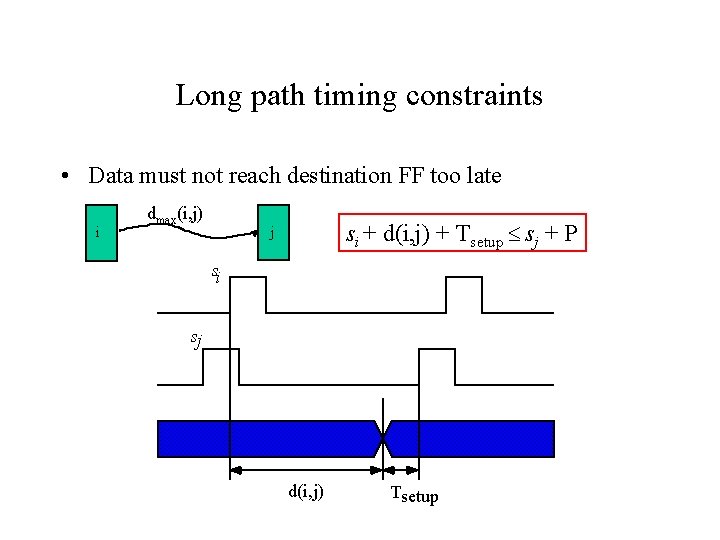
Long path timing constraints • Data must not reach destination FF too late i dmax(i, j) si + d(i, j) + Tsetup sj + P j si sj d(i, j) Tsetup

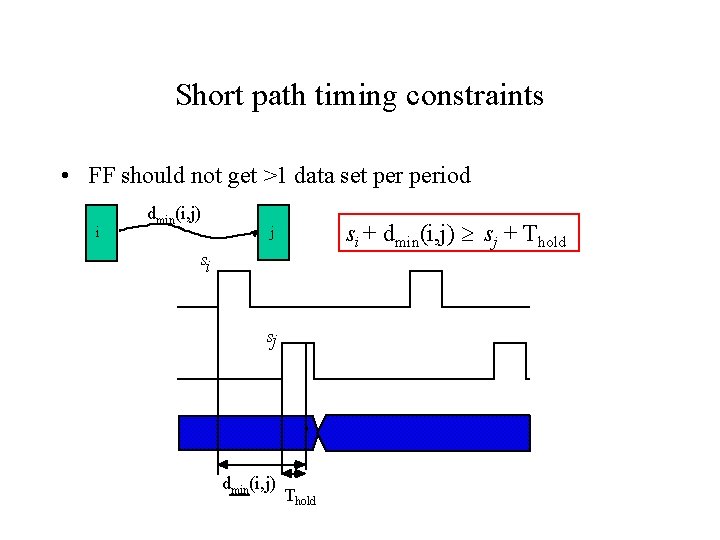
Short path timing constraints • FF should not get >1 data set period i dmin(i, j) si + dmin(i, j) sj + Thold j si sj dmin(i, j) Thold

Clock skew optimization • Another approach for sequential timing optimization • Deliberately change the arrival times of the clock at various memory elements in a circuit for cycle borrowing – For zero skew, delay from clock source to all FF’s = T – Positive skew of at FFk • Change delay from clock source to FFk to T + – Negative skew of at FFk • Change delay from clock source to FFk to T – • Problem statement: set skews for optimized performance

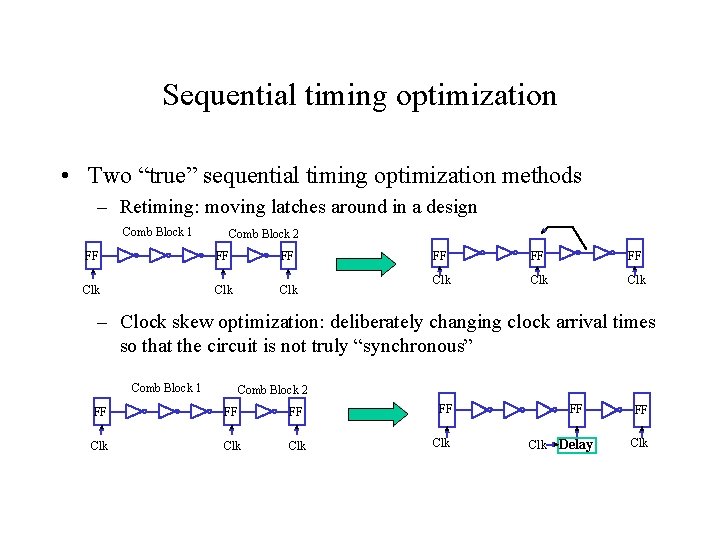
Sequential timing optimization • Two “true” sequential timing optimization methods – Retiming: moving latches around in a design Comb Block 1 Comb Block 2 FF FF FF Clk Clk Clk – Clock skew optimization: deliberately changing clock arrival times so that the circuit is not truly “synchronous” Comb Block 1 Comb Block 2 FF FF Clk Clk Clk FF FF Delay Clk

Finding the optimal clock period using skews • Represented by the optimization problem below - solve for P and optimal skews minimize P subject to (for all pairs of FF’s (i, j) connected by a combinational path) si + dmin(i, j) sj + Thold si + dmax(i, j) + Tsetup sj + P • If dmax(i, j) and dmin(i, j) are constant – linear program in the variables si and P

Graph-based approaches • For a constant clock period P, the linear program = system of difference constraints sp - sq constant • As before, perform a binary search on P • For each value of P build an equivalent constraint graph i f(P) j • Shortest path in the constraint graph gives a set of skews for a given value of P • If P is infeasible, there will be a negative cycle in the graph that will be detected during shortest-path calculations

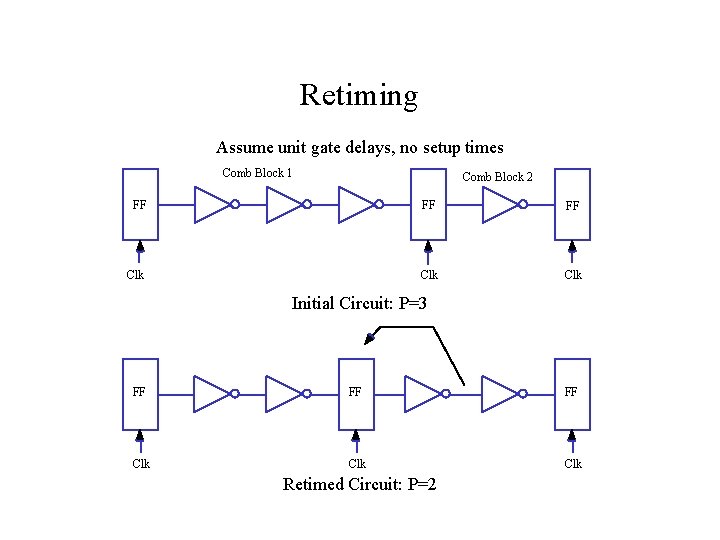
Retiming Assume unit gate delays, no setup times Comb Block 1 Comb Block 2 FF FF FF Clk Clk Initial Circuit: P=3 FF FF FF Clk Clk Retimed Circuit: P=2

Retiming: Definition • Relocation of flip-flops (FF’s) and latches (usually to achieve lower clock periods) • Maintain the latency of all paths in circuit, i. e. , number of FF stages on any input-output path must remain unchanged

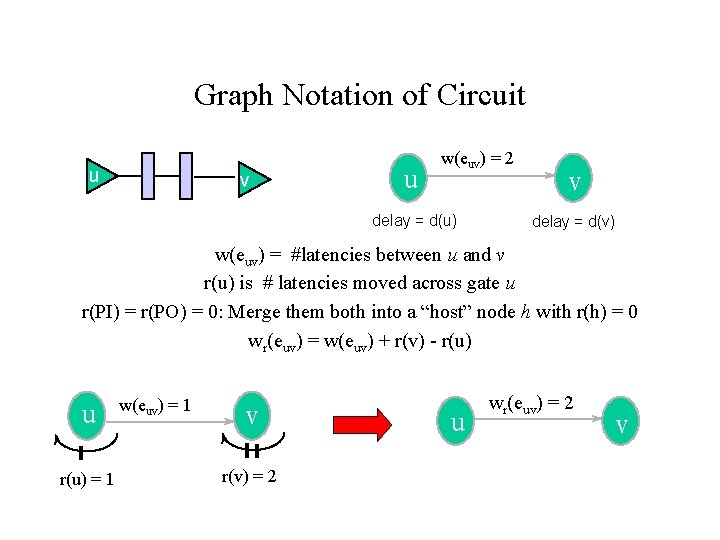
Graph Notation of Circuit u v u w(euv) = 2 delay = d(u) v delay = d(v) w(euv) = #latencies between u and v r(u) is # latencies moved across gate u r(PI) = r(PO) = 0: Merge them both into a “host” node h with r(h) = 0 wr(euv) = w(euv) + r(v) - r(u) u r(u) = 1 w(euv) = 1 v r(v) = 2 u wr(euv) = 2 v

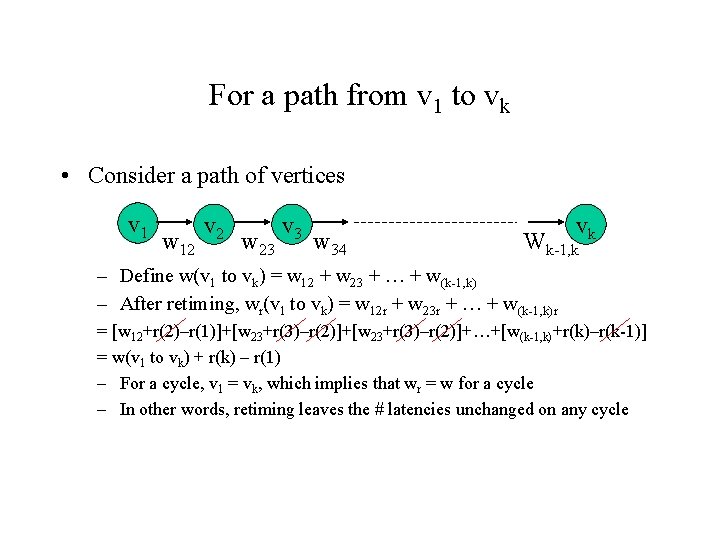
For a path from v 1 to vk • Consider a path of vertices v 1 w 12 v 2 w 23 v 3 w 34 vk Wk-1, k – Define w(v 1 to vk) = w 12 + w 23 + … + w(k-1, k) – After retiming, wr(v 1 to vk) = w 12 r + w 23 r + … + w(k-1, k)r = [w 12+r(2)–r(1)]+[w 23+r(3)–r(2)]+…+[w(k-1, k)+r(k)–r(k-1)] = w(v 1 to vk) + r(k) – r(1) – For a cycle, v 1 = vk, which implies that wr = w for a cycle – In other words, retiming leaves the # latencies unchanged on any cycle

Constraints for retiming • Non-negativity constraints (cannot have negative latencies) – wr on each edge must be non-negative – For any edge from vertex u to vertex v, wr(u, v) = w(u, v) + r(v) – r(u) 0 i. e. , r(u) – r(v) w(u, v) • Period constraints (need a latency if path delay period) – (or more precisely, path delay + Tsetup period) – For any path from vertex v 1 to vertex vk, under clock period P, wr(v 1 to vk) = w(v 1 to vk) + r(vk) – r(v 1) 1 if delay(v 1 to vk) > P i. e. , r(v 1) – r(vk) w(v 1 to vk) – 1 if delay(v 1 to vk) > P

Comb Block 1 FF Example G 2 G 1 • – Vertex weights = gate delays – Edge weights = # latencies 0 h 0 0 0 G 2 1 1 0 1 G 3 G 4 Non-negativity constraints 1. 2. 3. 4. 5. • 1 G 4 G 1 1 G 3 FF Clk • Circuit graph: Comb Block 2 r(h) – r(G 1) 0 r(G 1) – r(G 2) 0 r(G 2) – r(G 3) 0 r(G 3) – r(G 4) 1 r(G 4) – r(h) 0 Period constraints for P = 2 6. 7. 8. 9. r(h) – r(G 3) -1 r(G 1) – r(G 3) -1 r(G 2) – r(G 4) 0 r(G 2) – r(h) 0 FF Clk

Graph-based approaches • System of difference constraints r(u) – r(v) c • Equivalent constraint graph v c u • Shortest path in the constraint graph gives a set of valid r values for a given value of P (note that period constraints change for different values of P) • If P is infeasible, there will be a negative cycle in the graph that will be detected during shortest-path calculations

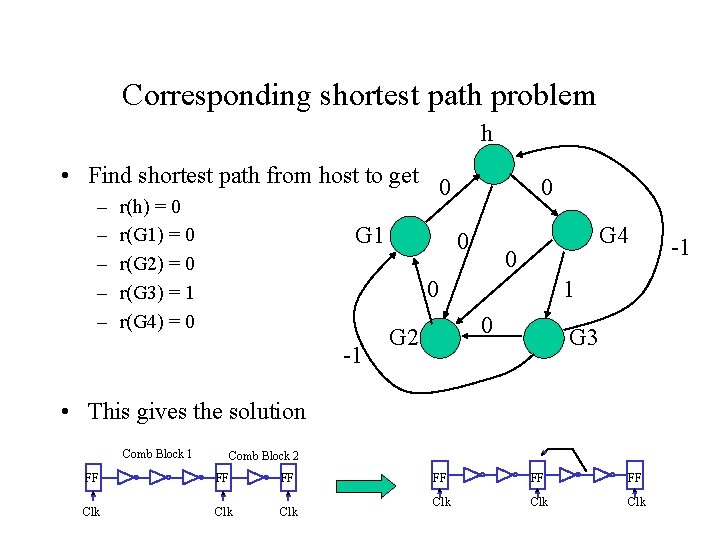
Corresponding shortest path problem h • Find shortest path from host to get 0 – – – r(h) = 0 r(G 1) = 0 r(G 2) = 0 r(G 3) = 1 r(G 4) = 0 G 1 0 0 G 4 0 0 -1 1 0 G 2 G 3 • This gives the solution Comb Block 1 Comb Block 2 FF FF FF Clk Clk Clk -1

Overall scheme for minimum period retiming • Objective: to find a retiming that minimizes the clock period (the assignment of r values may not be unique due to slack in the shortest path graph!) – – Binary search over P = [0, Punretimed] Punretimed = period of unretimed circuit = upper bound on optimal P Range in some iteration of the search = [Pmin, Pmax] Build shortest path graph with non-negativity constraints (independent of P) – At each value of P • Add period constraints to shortest path graph (related to W, D matrices discussed in class – will not describe here) • Solve shortest path problem • If negative cycle found, set Pmin = P; else set Pmax = P • Iterate until range of P is sufficiently small

Finding shortest paths • Dijkstra’s algorithm – O(Vlog. V + E) for a graph with V vertices and E edges – Applicable only if all edge weights are non-negative – The latter condition does not hold in our case! • Bellman-Ford algorithm – O(VE) for a graph with V vertices and E edges – Outline for I = 1 to V – 1 for each edge (u, v) E update neighbor’s weights as r(v) = min[r(u) + d(u, v), r(v)] for each edge (u, v) E if r(u) + d(u, v) > r(v) then a negative cycle exists • Basic idea: in iteration I, update lowest cost path with I edges • After V – 1 iterations, if any update is still required, a negative cycle exists

“Relaxation” algorithm for retiming • • Perform a binary search on clock period P as before At each value of P check feasibility as follows – Repeat V-1 times (where V = # vertices) 1. 2. 3. 4. 5. Set r(u) = 0 for each vertex Perform timing analysis to find clock period of the circuit For any vertex u with delay > P, r(u)++ If no such vertex exists, P is feasible Else, retime the circuit using these values of r; update the circuit and go to step 1 – If Clock period > P after V – 1 iterations, then P is infeasible

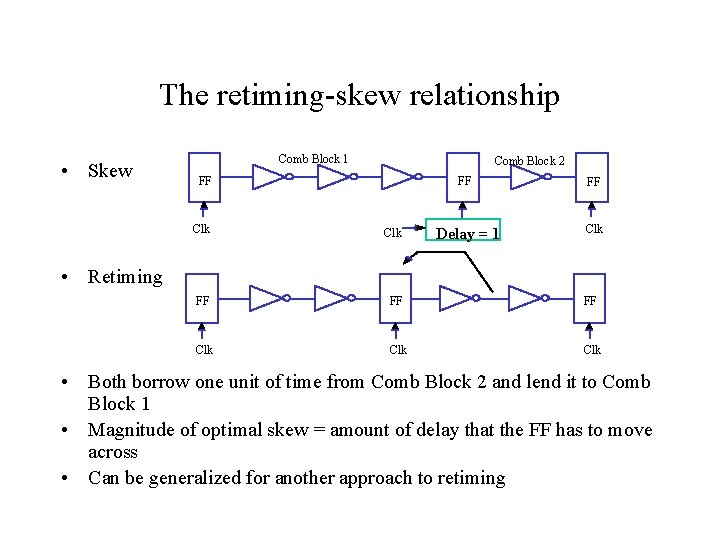
The retiming-skew relationship • Skew Comb Block 1 Comb Block 2 FF FF FF Delay = 1 Clk Clk FF FF FF Clk Clk • Retiming • Both borrow one unit of time from Comb Block 2 and lend it to Comb Block 1 • Magnitude of optimal skew = amount of delay that the FF has to move across • Can be generalized for another approach to retiming

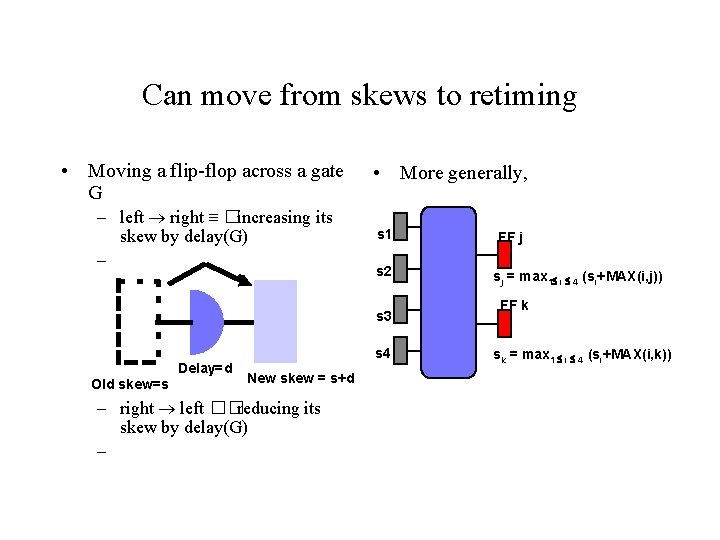
Can move from skews to retiming • Moving a flip-flop across a gate G – left right �increasing its skew by delay(G) – • More generally, s 1 s 2 s 3 Delay=d Old skew=s s 4 New skew = s+d – right left ��reducing its skew by delay(G) – FF j sj = max 1 i 4 (si+MAX(i, j)) FF k sk = max 1 i 4 (si+MAX(i, k))

Another approach to retiming • Two-phase approach – Phase A: Find optimal skews (complexity depends on the number of FF’s, not the number of gates) – Phase B: Relocate FF’s to retime circuit (since most FF movements are seen to be local in practice, this does not take too long) – Not provably better than earlier approach in terms of complexity, but practically works very well