Sec 1 2 Roundoff Errors and Computer Arithmetic

Sec: 1. 2 Round-off Errors and Computer Arithmetic

Sec: 1. 2 Round-off Errors and Computer Arithmetic The purpose of this section is to study how errors in numbers can propagate through mathematical functions. Example: Why? round-off errors are directly related to the manner in which numbers are stored in a computer. *numbers on the computer are represented with a binary, or base-2, system. Error = 0. 00000004 >> format short >> pi 3. 1416 >> format long >> pi 3. 141592653589793

Sec: 1. 2 Round-off Errors and Computer Arithmetic Binary Machine Numbers (floating-point number) In a computer, only a relatively small subset of the real number system is used for the representation of all the real numbers. Real line A 64 -bit (binary digit) representation c s Example: 0 1000011 10111001000000000000000000000 1 st 11 -bit sign characteristic exponent In 1985, the IEEE (Institute for Electrical and Electronic Engineers) published a report called Binary Floating Point Arithmetic Standard 754– 1985. f 52 -bit mantissa fraction Example: 0 1000011 10111001000000000000000000000 This provides standards for binary and decimal floating point numbers, formats for data interchange, algorithms for rounding arithmetic operations, and for the handling of exceptions. single, double, precisions 1000011

Sec: 1. 2 Round-off Errors and Computer Arithmetic 11 -bit exponent 1000011 A 64 -bit (binary digit) representation s sign c 11 -bit exponent f 52 -bit fraction Example: 0 1000011 10111001000000000000000000000 52 -bit fraction 10111001000000000000000000000 0 1000011 10111001000000000000000000000 S=0 c = 1027

Sec: 1. 2 Round-off Errors and Computer Arithmetic Example: (similar to 15 a/29) Use the 64 -bit long real format to find the decimal equivalent of the following floating-point machine number. 0 0111110 100100110000000000000000000000 S=0 c = 2^9+2^8+2^7+2^6+2^5+2^4+2^3+2^2+2^1= 1022 = 0. 57421875 0 0111110 100100110000000000000000000000 Example: 1 0111110 100100110000000000000000000000

Sec: 1. 2 Round-off Errors and Computer Arithmetic Largest floating point 0 11111111111111111111111111111111 S =0 c = 2046 = 0. 1797693134862316 e+309 >> 2^1023*(2 -2^(-52)) 1. 797693134862316 e+308 >>2^1024 -2^971 Inf Numbers greater than result in overflow (Inf)

Sec: 1. 2 Round-off Errors and Computer Arithmetic 0 smallest normalized positive number S=0 c=1 = 2. 225073858507201 e-308 Numbers occurring in calculations that have a magnitude less than result in underflow and are generally set to zero

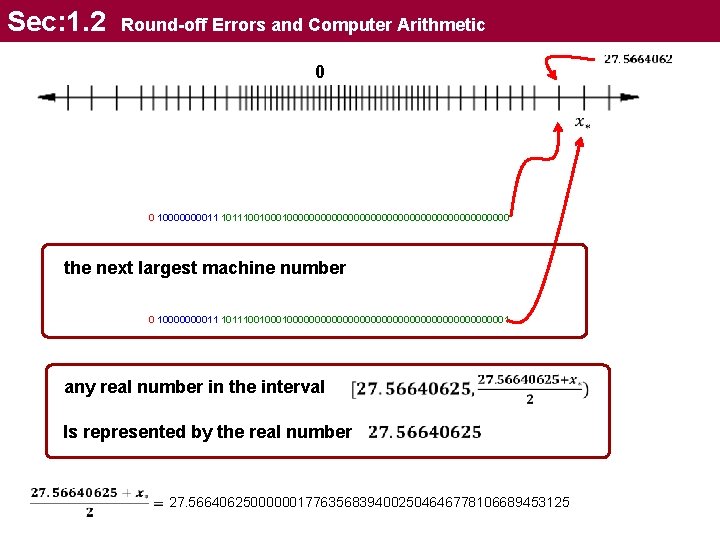
Sec: 1. 2 Round-off Errors and Computer Arithmetic 0 0 1000011 10111001000000000000000000000 the next largest machine number 0 1000011 10111001000000000000000000001 any real number in the interval Is represented by the real number 27. 5664062500000017763568394002504646778106689453125

Sec: 1. 2 Round-off Errors and Computer Arithmetic Decimal Machine Numbers we assume that machine numbers are represented in the normalized decimal floating-point form Binary Machine Numbers (floating-point number) s Example: 5 -digit decimal machine numbers The floating-point form of y, denoted fl(y), is obtained by terminating the mantissa of y at k decimal digits. two common ways of termination chopping rounding Example: chopping rounding c f

Sec: 1. 2 Round-off Errors and Computer Arithmetic Example: Determine the absolute and relative errors chopping rounding two methods for measuring approximation errors Remark As a measure of accuracy, the absolute error can be misleading and the relative error more meaningful, because the relative error takes into consideration the size of the value. significant digits (or figures)

Sec: 1. 2 Round-off Errors and Computer Arithmetic significant digits (or figures) Example: Determine the significant digits

Sec: 1. 2 Round-off Errors and Computer Arithmetic Finite-Digit Arithmetic Source of round-off error: number repersentations, arithmetic operations Example: x ⊕ y = fl(fl(x) + fl(y)), Example:

Sec: 1. 2 Round-off Errors and Computer Arithmetic Nested Arithmetic round-off error can also be reduced by rearranging calculations Example: Evaluate f (x) at x = 4. 71 using three-digit arithmetic. Exact: f (4. 71)= − 14. 263899 Remark The relative errors Three-digit (chopping): f (4. 71) = − 13. 5 0. 05 Three-digit (rounding): 0. 06 f (4. 71)= − 13. 4 Three-digit (chopping): f (4. 71) = − 14. 2 0. 0045 Three-digit (rounding): 0. 0025 f (4. 71)= − 14. 3 The decreased error in this example is due to the reduction in computations from four multiplications and three additions to two multiplications and three additions. One way to reduce round-off error is to reduce the number of computations. Polynomials should always be expressed in nested form

Sec: 1. 2 Round-off Errors and Computer Arithmetic rationalizing the numerator round-off error can also be reduced by rearranging calculations Example: The relative errors Remark 0. 24 0. 00062 1) the subtraction of nearly equal numbers, 2) the division by small number (x 2)