Salvador Amaya 9 5 Polygons Polygons A polygon













































- Slides: 73

Salvador Amaya 9 -5 Polygons

Polygons �A polygon is a closed figure that has no curved sides. Therefore, it needs to have at least three sides. Not a polygon Yes, a polygon

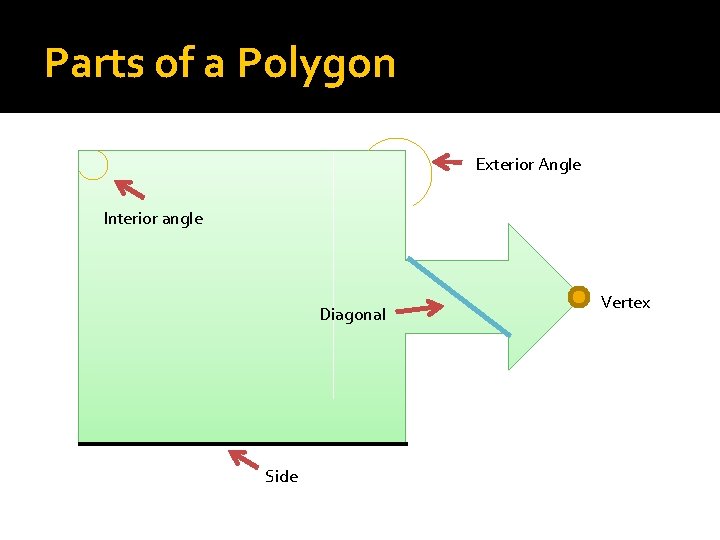
Parts of a Polygon Exterior Angle Interior angle Diagonal Side Vertex

Parts of a Polygon (ctd) �Interior angle: angle in the inside of a polygon �Exterior angle: angle in the outside of a polygon �Vertex: point where two lines meet �Diagonal: segment that connects two vertices of a polygon �Side: segment in a polygon

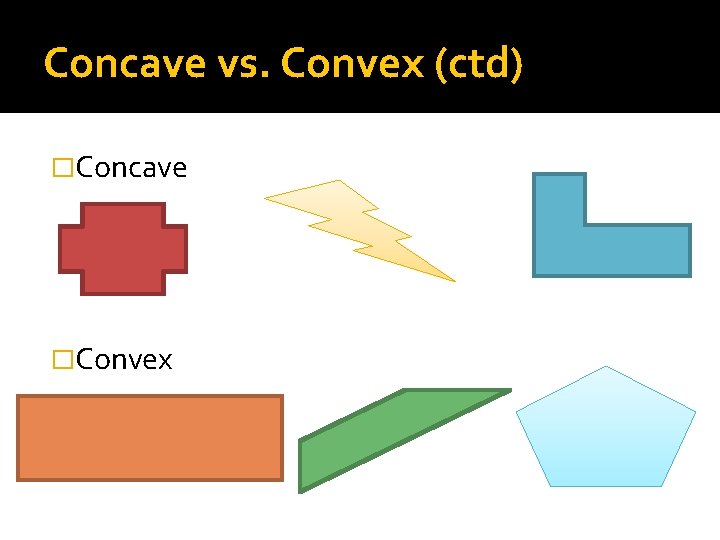
Concave vs. Convex �Concave polygon: polygon that has a vertex that points in �Convex polygon: polygon that has all vertices pointing out.

Concave vs. Convex (ctd) �Concave �Convex

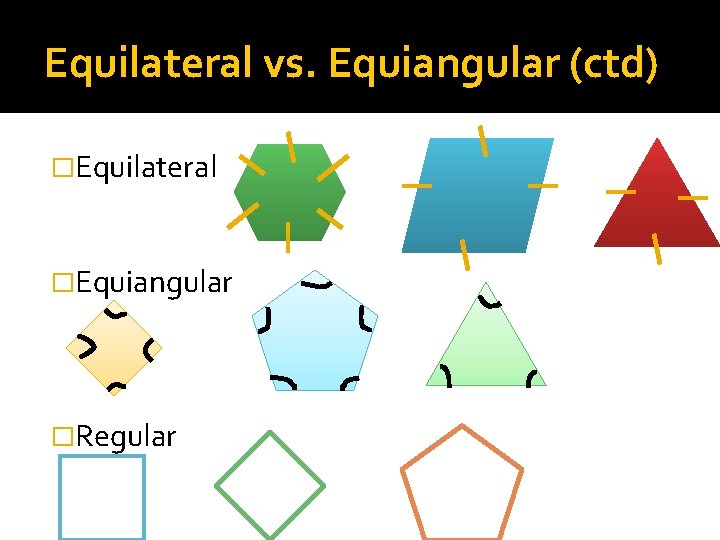
Equilateral vs. Equiangular �Equilateral: All sides measure the same. �Equiangular: All the angles measure the same. �Equilateral and Equiangular = Regular Polygon

Equilateral vs. Equiangular (ctd) �Equilateral �Equiangular �Regular

Interior Angles Theorem for Polygons �The sum of the interior angles of a polygon is (n-2) x 180, being n the number of sides in the polygon.

Interior Angles Theorem for Polygons (ctd) �What is the sum of interior angles for a nonagon? �(n-2) x 180 �(9 -2) x 180 � 7 x 180 � 1260

Interior Angles Theorem for Polygons (ctd) �What is the measure of an angle in a regular hexagon? �[(n-2) x 180] / n �[(6 -2) x 180] / 6 �(4 x 180) / 6 � 720 / 6 � 120

Interior Angles Theorem for Polygons (ctd) �What is the sum of the interior angles for a pentagon? �(n-2) x 180 �(5 -2) x 180 � 3 x 180 � 540

Theorems for Parallelograms: Sides �If a quadrilateral is a parallelogram, then opposite sides are congruent.

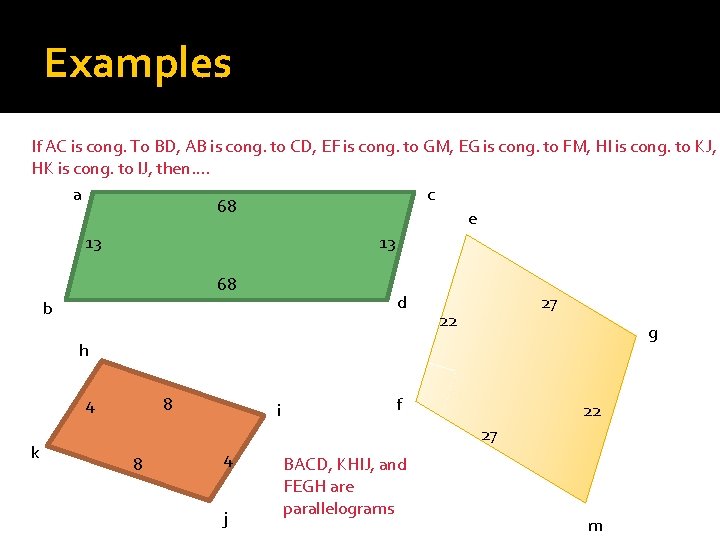
Examples If BACD, KHIJ, and FEGH are parallelograms, then…. a c e d b AC is cong. To BD, AB is cong. to CD, EF is cong. to GM, EG is cong. to FM, HI is cong. to KJ, HK is cong. to IJ. g h i f k j m

Theorems for Parallelograms , converse : Sides �If opposite sides in a quadrilateral are congruent, then the quadrilateral is a parallelogram.

Examples If AC is cong. To BD, AB is cong. to CD, EF is cong. to GM, EG is cong. to FM, HI is cong. to KJ, HK is cong. to IJ, then…. a c 68 e 13 13 68 d b 27 22 g h 4 k 8 i f 22 27 8 4 j BACD, KHIJ, and FEGH are parallelograms m

Theorems for Parallelograms: Angles �If a quadrilateral is a parallelogram, then opposite angles are congruent.

Examples If BACD, KHIJ, and FEGH are parallelograms, then…. a c e <a is cong. to <d, <c is cong. to <b, <e is cong. to <m, <f is cong. to < g, <h is cong. to <j, <k is cong. to <i d b g h i f k j m

Theorems for Parallelograms, converse: Angles �If opposite angles are congruent in a quadrilateral, then the quadrilateral is a parallelogram.

Examples If <a is cong. to <d, <c is cong. to <b, <e is cong. to <m, <f is cong. to < g, <h is cong. to <j, <k is cong. to <i, then…. a 128 52 c e 36 52 128 b d 144 h 97 k 83 83 97 j i f 144 BACD, KHIJ, and FEGH are parallelograms 36 m g

Theorems for Parallelograms: Angles 2 �If a quadrilateral is a parallelogram, then the consecutive angles add up to 180.

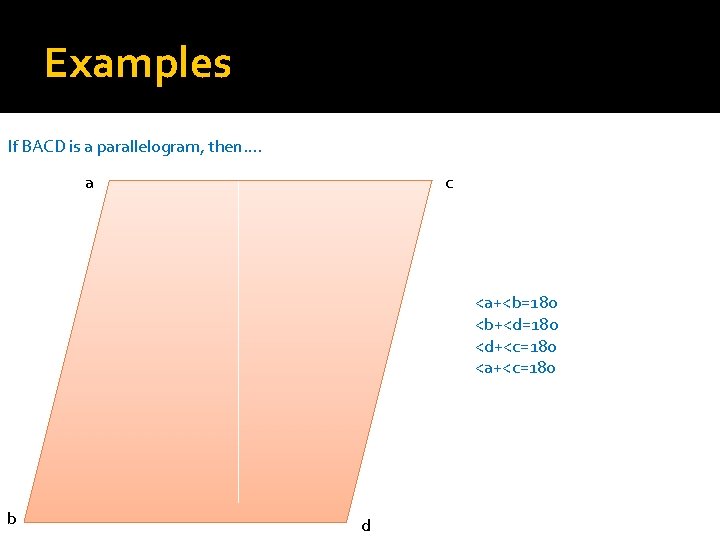
Examples If BACD is a parallelogram, then…. a c <a+<b=180 <b+<d=180 <d+<c=180 <a+<c=180 b d

Theorems for Parallelograms, converse: Angles 2 �If the consecutive angles in a quadrilateral add up to 180, then the quadrilateral is a parallelogram

Examples If <a+<b=180, <a+<c=180, <b+<c=180, <d+<c=180, <e+<g=180, <e+<f=180, <g+<m=180, <m+<f=180, <h+<i=180, <h+<k=180, <k+<j=180, <j+<i=180, then…. a 135 65 c e 24 65 135 b d 156 h 103 k 77 77 103 j i f 156 BACD, KHIJ, and FEGH are parallelograms 24 m g

Theorems for Parallelograms: Diagonals �If a quadrilateral is a parallelogram, then the diagonals bisect each other.

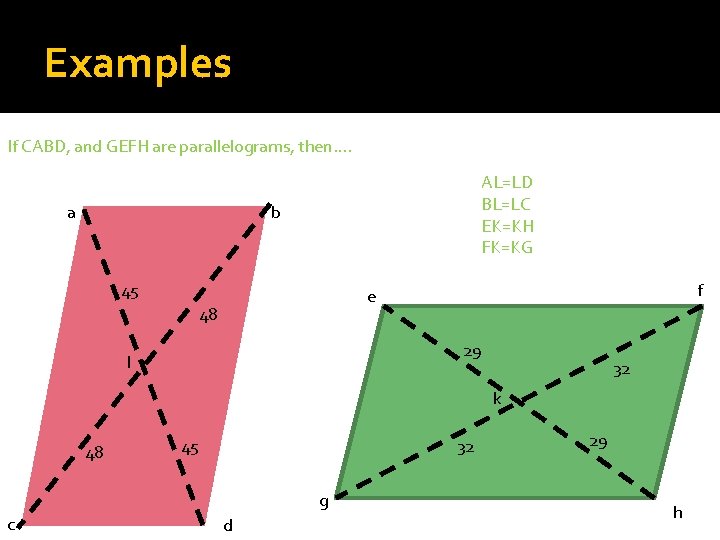
Examples If CABD, and GEFH are parallelograms, then…. a AL=LD BL=LC EK=KH FK=KG b 45 f e 48 29 l 32 k 48 45 32 g c d 29 h

How to prove that a quadrilateral is a parallelogram �Both pairs of opposite sides are congruent. �Both pairs of opposite angles are congruent. �Its consecutive angles are supplementary. �Its diagonals bisect each other. �It has a pair of congruent parallel sides. �Both pairs of opposite sides are parallel.

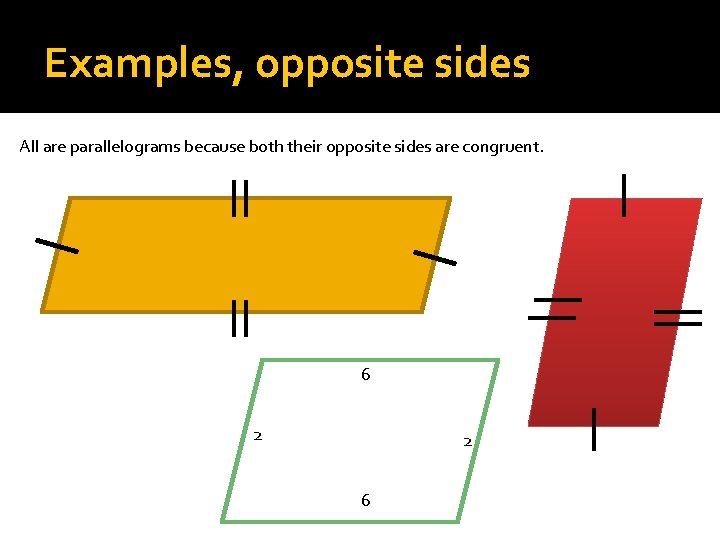
Examples, opposite sides All are parallelograms because both their opposite sides are congruent. 6 2 2 6

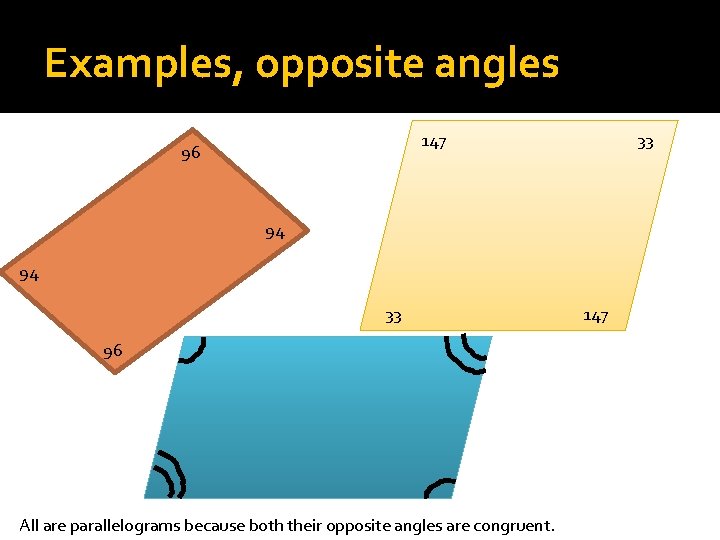
Examples, opposite angles 147 96 33 94 94 33 96 All are parallelograms because both their opposite angles are congruent. 147

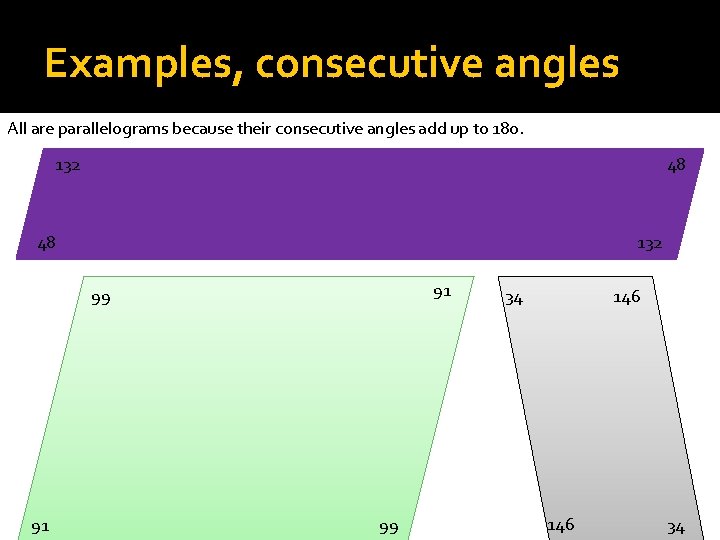
Examples, consecutive angles All are parallelograms because their consecutive angles add up to 180. 132 48 48 132 91 99 34 146 34

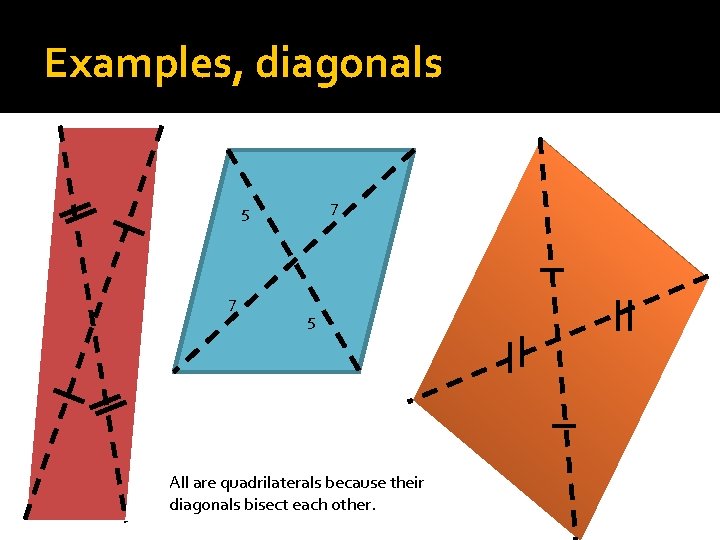
Examples, diagonals 7 5 All are quadrilaterals because their diagonals bisect each other.

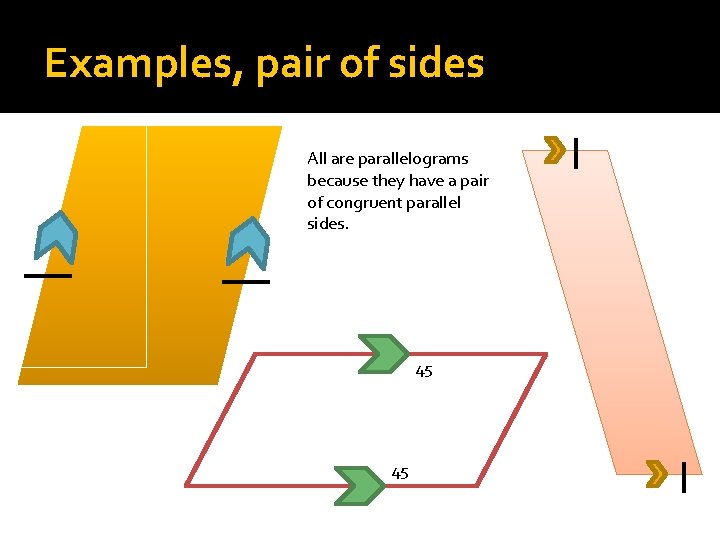
Examples, pair of sides All are parallelograms because they have a pair of congruent parallel sides. 45 45

Examples, parallel sides

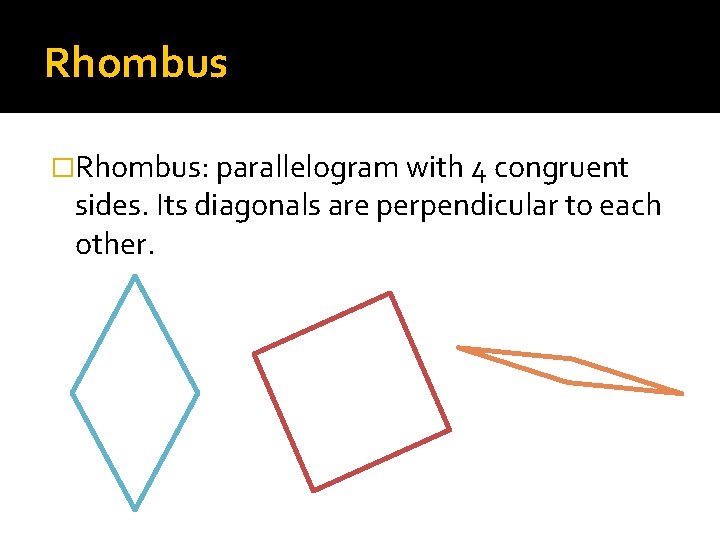
Rhombus �Rhombus: parallelogram with 4 congruent sides. Its diagonals are perpendicular to each other.

Rhombus Theorems �If a quadrilateral is a rhombus, then it is a parallelogram.

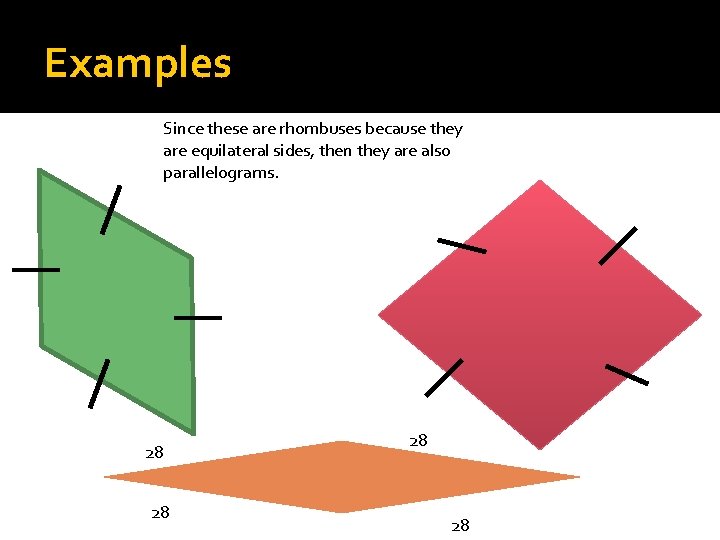
Examples Since these are rhombuses because they are equilateral sides, then they are also parallelograms. 28 28

Rhombus Theorems (ctd) �If a parallelogram is a rhombus, then its diagonals are perpendicular to each other.

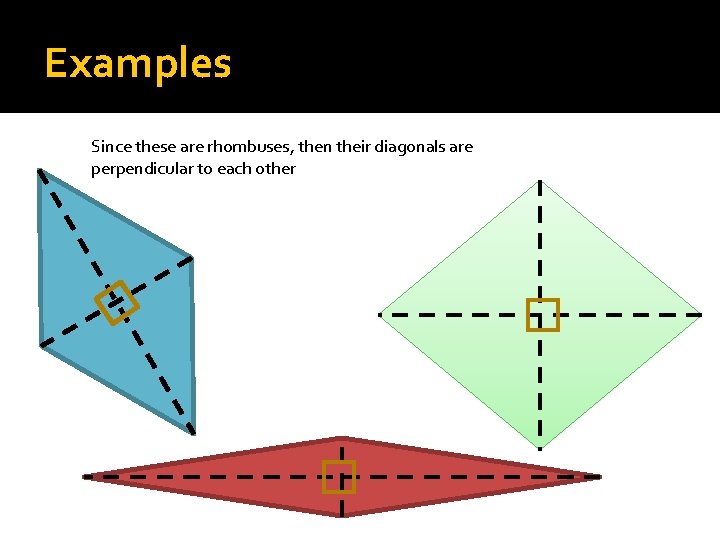
Examples Since these are rhombuses, then their diagonals are perpendicular to each other

Rhombus Theorems (ctd) �If a parallelogram is a rhombus, then their diagonals bisect the opposite angles.

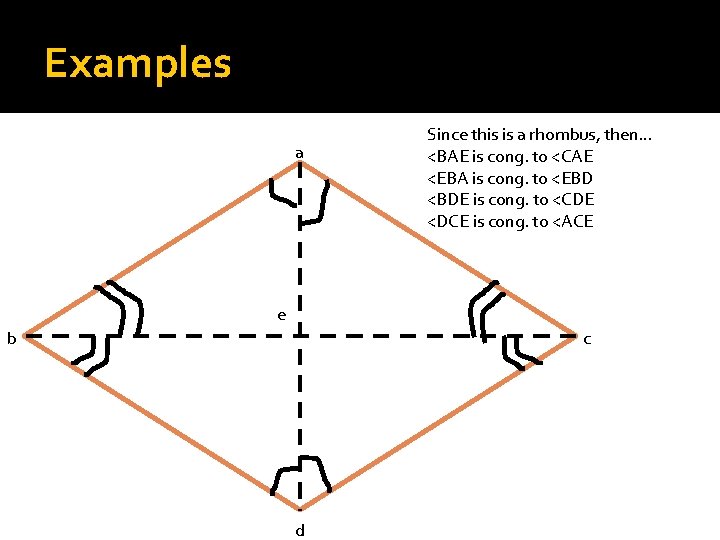
Examples a Since this is a rhombus, then… <BAE is cong. to <CAE <EBA is cong. to <EBD <BDE is cong. to <CDE <DCE is cong. to <ACE e b c d

Rhombus Theorems (ctd) �If a pair of consecutive sides is congruent, then the quadrilateral is a rhombus.

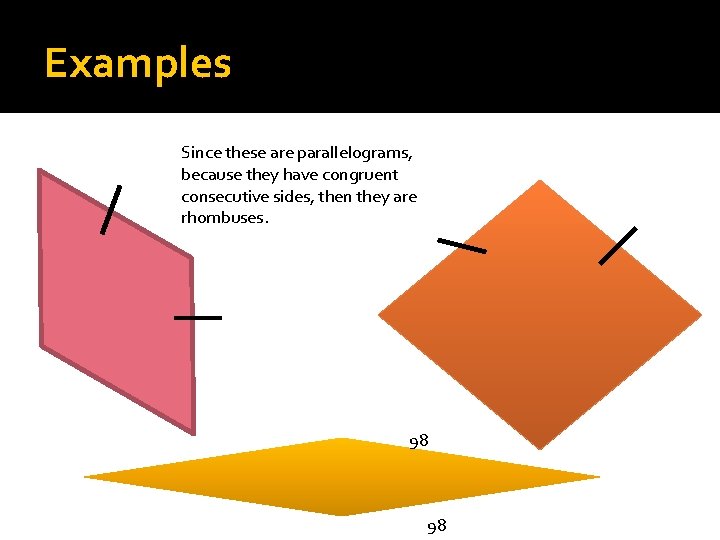
Examples Since these are parallelograms, because they have congruent consecutive sides, then they are rhombuses. 98 98

Rhombus Theorems (ctd) �If the diagonals in a parallelogram are perpendicular, then it is a rhombus.

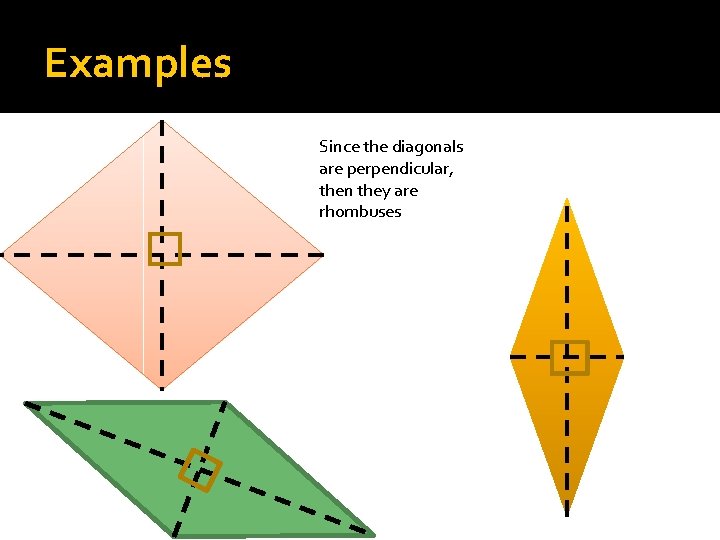
Examples Since the diagonals are perpendicular, then they are rhombuses

Rhombus Theorems (ctd) �If a diagonal bisects a pair of opposite angles, then it is a rhombus.

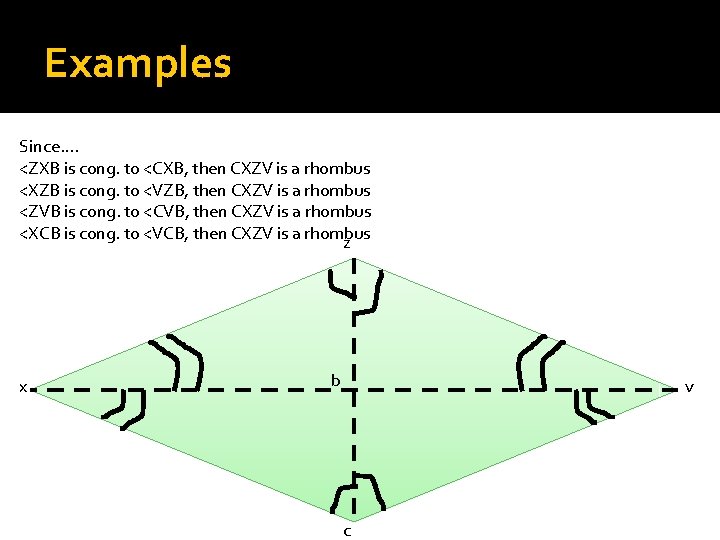
Examples Since…. <ZXB is cong. to <CXB, then CXZV is a rhombus <XZB is cong. to <VZB, then CXZV is a rhombus <ZVB is cong. to <CVB, then CXZV is a rhombus <XCB is cong. to <VCB, then CXZV is a rhombus z x b v c

Rectangle �Rectangle: parallelogram with 4 right angles. Its diagonals are congruent.

Rectangle Theorems �If it is a rectangle, then it is a parallelogram.

Examples Since these are rectangles (4 rt. angles), then they are also parallelograms.

Rectangle Theorems (ctd) �If it is a rectangle, then the diagonals are congruent.

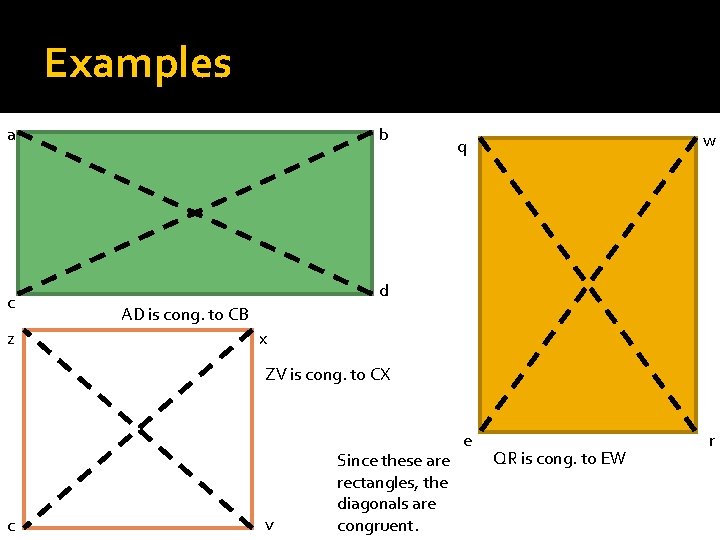
Examples a c z b w q d AD is cong. to CB x ZV is cong. to CX c v Since these are rectangles, the diagonals are congruent. e QR is cong. to EW r

Rectangle Theorems (ctd) �If a quadrilateral has a right angle, then it is a rectangle.

Examples They are all rectangles because they each have a right angle.

Rectangle Theorems (ctd) �If the diagonals in a parallelogram are congruent, then it is a rectangle.

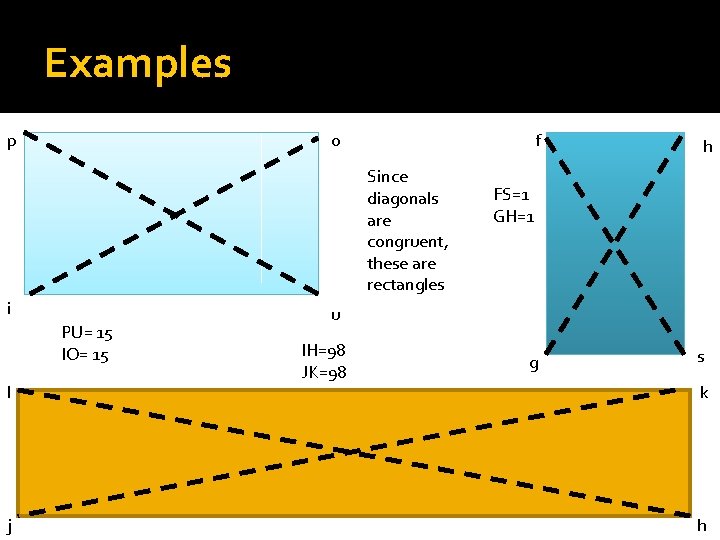
Examples p o f Since diagonals are congruent, these are rectangles i PU= 15 IO= 15 l j h FS=1 GH=1 u IH=98 JK=98 g s k h

Square �Square: parallelogram with 4 sides that are congruent and angles are congruent. The diagonals are congruent and perpendicular. �It is both a rhombus and a rectangle.

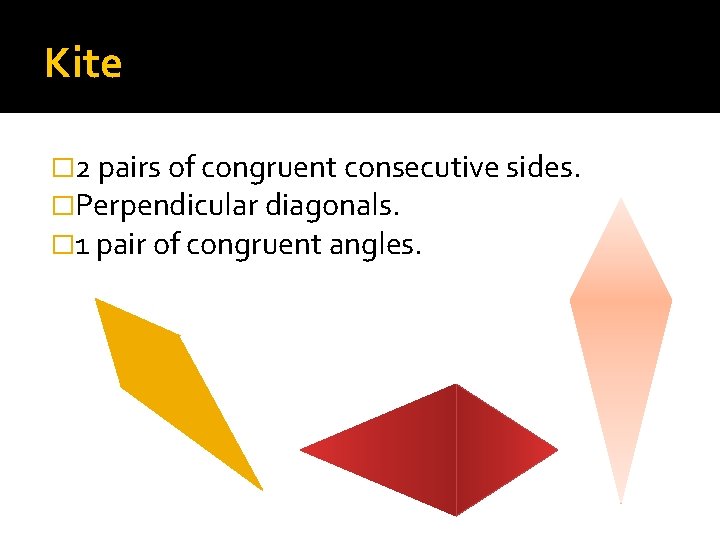
Kite � 2 pairs of congruent consecutive sides. �Perpendicular diagonals. � 1 pair of congruent angles.

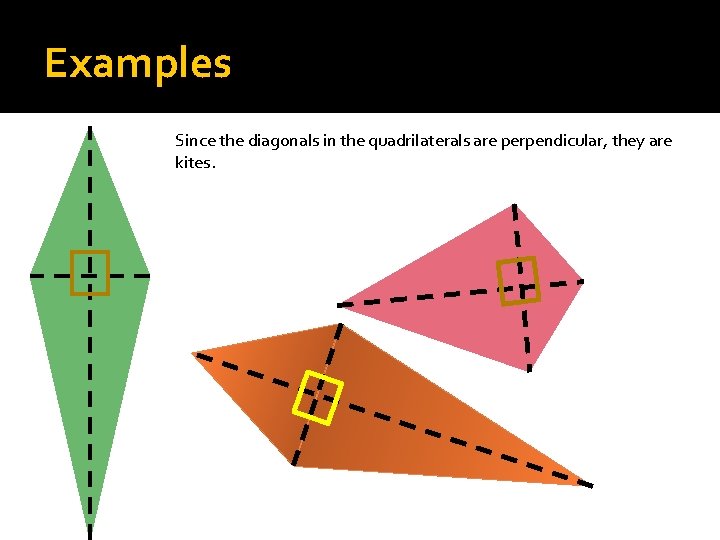
Kite Theorems �If it is a kite, then diagonals are perpendicular.

Examples Since the diagonals in the quadrilaterals are perpendicular, they are kites.

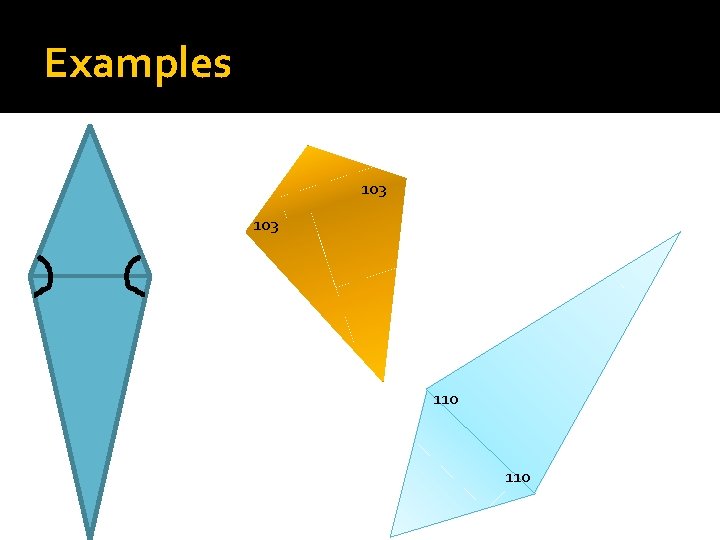
Kite Theorems (ctd) �If it is a kite, then there is 1 pair of opposite congruent angles.

Examples 103 110

Trapezoid �One pair of parallel sides. �Base- nonparallel side �Leg- parallel side. �Base angles- angles whose common side is a base. �Isosceles trapezoid- has 2 congruent legs

Isosceles Trapezoid Theorems �If it is an isosceles trapezoid, then the 2 pairs of base angles are congruent.

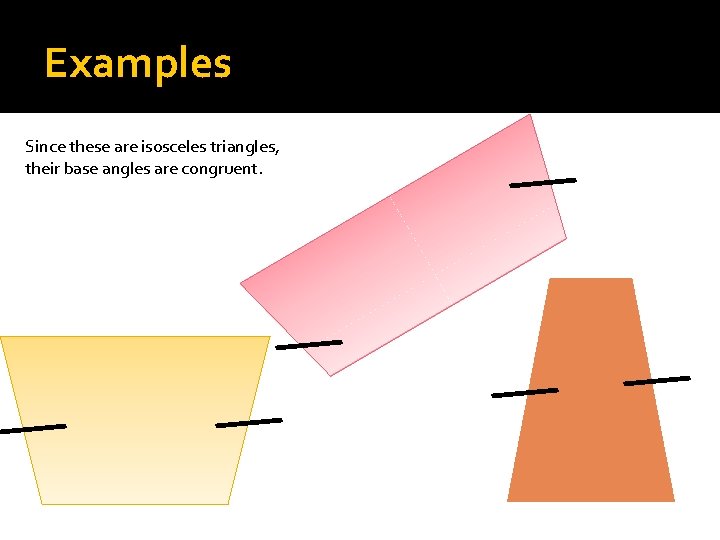
Examples Since these are isosceles triangles, their base angles are congruent.

Isosceles Trapezoid Theorems (ctd) �If there are 2 pairs of congruent angles, base angles, it is an isosceles triangle.

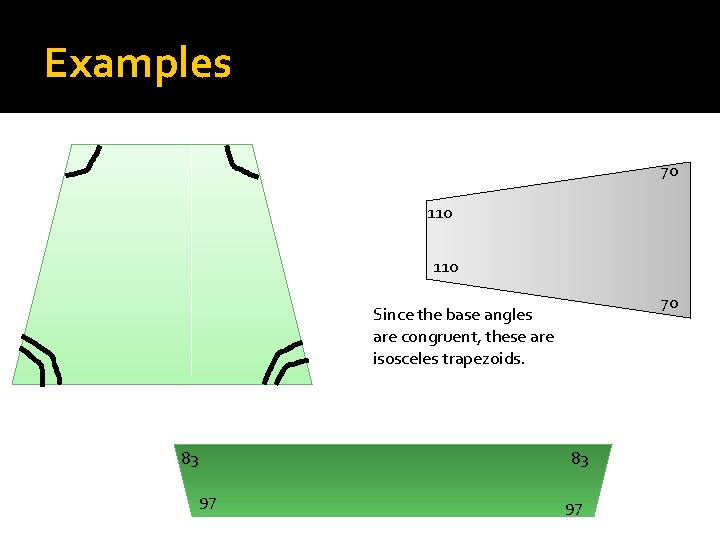
Examples 70 110 70 Since the base angles are congruent, these are isosceles trapezoids. 83 83 97 97

Isosceles Trapezoid Theorems (ctd) �An isosceles trapezoid has to have congruent diagonals.

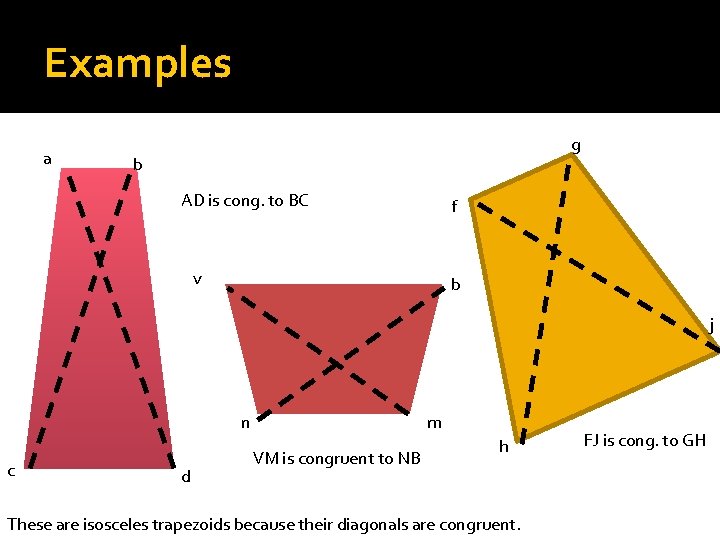
Examples a g b AD is cong. to BC f v b j n c d m VM is congruent to NB h These are isosceles trapezoids because their diagonals are congruent. FJ is cong. to GH

Trapezoid Midsegment Theorem �The midsegment in a trapezoid is parallel to both bases and it is half as long as the sum of the two other bases. �(b 1+b 2)/2

Examples �What is the midsegment of this trapezoid? �(b 1+b 2)/2 10 � 10+35/2 � 45/2 � 22. 5 35

Examples �What is the measure of the missing base? � 67 -21= 46 � 46+67= 113 21 67

Examples �What is the midsegment of this trapezoid? �(b 1+b 2)/2 135 � 135+11/2 � 146/2 � 73 11

_____(0 -10 pts. ) Describe what a polygon is. Include a discussion about the parts of a polygon. Also compare and contrast a convex with a concave polygon. Compare and contrast equilateral and equiangular. Give 3 examples of each. _____(0 -10 pts. ) Explain the Interior angles theorem for polygons. Give at least 3 examples. _____(0 -10 pts. ) Describe the 4 theorems of parallelograms and their converse and explain how they are used. Give at least 3 examples of each. _____(0 -10 pts. ) Describe how to prove that a quadrilateral is a parallelogram. Give at least 3 examples of each. _____(0 -10 pts. ) Compare and contrast a rhombus with a square with a rectangle. Describe the rhombus, square and rectangle theorems. Give at least 3 examples of each. _____(0 -10 pts. ) Describe a trapezoid. Explain the trapezoidal theorems. Give at least 3 examples of each. _____(0 -10 pts. ) Describe a kite. Explain the kite theorems. Give at least 3 examples of each.
 Orlando amaya
Orlando amaya Amaya casnav
Amaya casnav Amaya valdemoro edad
Amaya valdemoro edad Traducior
Traducior Materiales amaya
Materiales amaya Texte informatif exercices secondaire
Texte informatif exercices secondaire Barroco tablerado en mexico
Barroco tablerado en mexico Not polygon
Not polygon How to tell if shapes are similar
How to tell if shapes are similar Que producto exporta el salvador
Que producto exporta el salvador Quienes son los comerciantes sociales
Quienes son los comerciantes sociales Cuando nacio salvador dali
Cuando nacio salvador dali Historia del comercio electrónico en el salvador
Historia del comercio electrónico en el salvador Young salvador dali
Young salvador dali Pablo picasso (1881-1973)
Pablo picasso (1881-1973) Salvador espriu frases
Salvador espriu frases Persistence of memory art style
Persistence of memory art style Salvador dali golden ratio
Salvador dali golden ratio Autoportrait mou avec lard grillé
Autoportrait mou avec lard grillé Renacempleo
Renacempleo Titulo de bachiller el salvador
Titulo de bachiller el salvador Abrazo salvador
Abrazo salvador Raisa salvador
Raisa salvador Vladimir kush
Vladimir kush Salvador dali prezentacja
Salvador dali prezentacja Villa el salvador
Villa el salvador Protocolo
Protocolo Cece el salvador
Cece el salvador Salvador dali georgia
Salvador dali georgia Universidad de el salvador facultad de ciencias economicas
Universidad de el salvador facultad de ciencias economicas Svnet
Svnet Afirmao
Afirmao Salvador carrillo ibero
Salvador carrillo ibero Nacimiento del cooperativismo
Nacimiento del cooperativismo Jesus é meu amigo, meu guia, meu senhor
Jesus é meu amigo, meu guia, meu senhor Personajes juan salvador gaviota
Personajes juan salvador gaviota Pinterest
Pinterest Salvador dali art movement
Salvador dali art movement Ceip salvador dali
Ceip salvador dali Sanitary registration in el salvador
Sanitary registration in el salvador Iglesia de san salvador la monera
Iglesia de san salvador la monera Salvador dali leganes
Salvador dali leganes Dali seven wonders of the world
Dali seven wonders of the world The second monday in october
The second monday in october Salvador dali nacio en
Salvador dali nacio en Dali ozelot
Dali ozelot Landscape near figueras (1910)
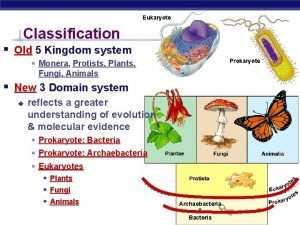
Landscape near figueras (1910) Monera vs prokaryotes
Monera vs prokaryotes Salvador late or early answer key
Salvador late or early answer key Persistence of memory art style
Persistence of memory art style Salvador perez camarena
Salvador perez camarena Adorai o rei do universo harpa cristã
Adorai o rei do universo harpa cristã Gure aita zeruetan zarana
Gure aita zeruetan zarana Oscar torres el salvador
Oscar torres el salvador Salvador dali manifesto atmosfera
Salvador dali manifesto atmosfera Mae west salvador dali
Mae west salvador dali La llegada del salvador
La llegada del salvador Working together rafael and salvador
Working together rafael and salvador Christus hypercubus salvador dali
Christus hypercubus salvador dali Gestin ins salvador dali
Gestin ins salvador dali Derecho mercantil en el salvador
Derecho mercantil en el salvador Salvador late or early questions
Salvador late or early questions El abrazo salvador
El abrazo salvador Mobilidade salvador
Mobilidade salvador Corpus hypercubus
Corpus hypercubus Salvador late or early theme
Salvador late or early theme Cuando nacio salvador dali
Cuando nacio salvador dali Tamales el salvador
Tamales el salvador Ali salvador
Ali salvador El salvador major landforms
El salvador major landforms Superior intercostal veins
Superior intercostal veins Pedro lizárraga osuna musician
Pedro lizárraga osuna musician Que es el cnp
Que es el cnp Educacion inclusiva en el salvador
Educacion inclusiva en el salvador