Rotations Geometry ROTATIONS A rotation is an isometric



















- Slides: 22

Rotations Geometry

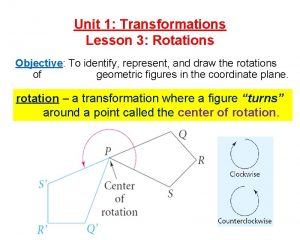
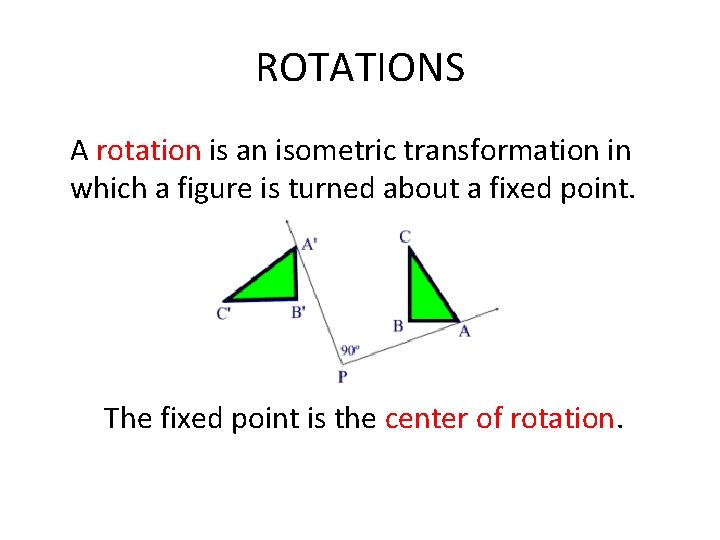
ROTATIONS A rotation is an isometric transformation in which a figure is turned about a fixed point. The fixed point is the center of rotation.

Angle of Rotation Rays drawn from the center of rotation to a point and its image form an angle called the angle of rotation.

Notation Rcenter, degree

Full Rotation One full rotation is ______°, this would return all points in the plane to their original location. Because a rotation can go in two directions along the same arc we need to define positive and negative rotation values.

Rotation Definition A rotation about a Point O through Ɵ degrees is an isometric transformation that maps every point P in the plane to a point P’, so that the following properties are true;

Rotation Definition 1. If point P is NOT point O, then OP = OP’ and m POP’ = Ɵ°.

Rotation Definition 2. If point P IS point O, then P = P’. The center of rotation is the ONLY point in the plane that is unaffected by a rotation.

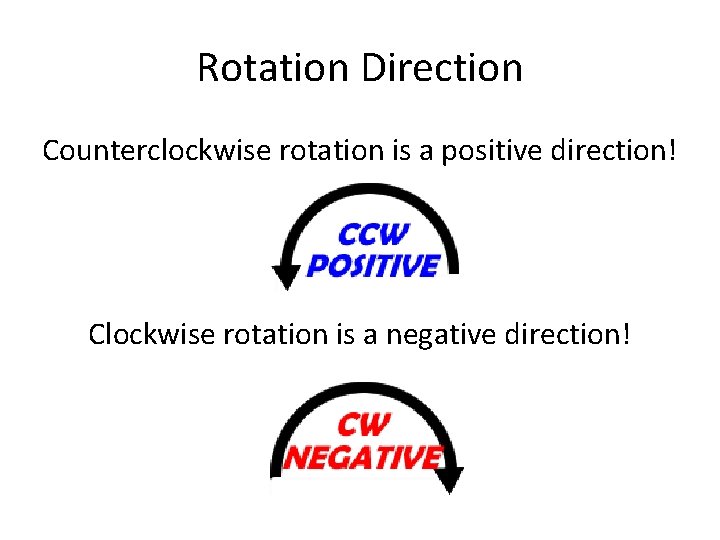
Rotation Direction Counterclockwise rotation is a positive direction! Clockwise rotation is a negative direction!

Equivalent Rotations Because angles are formed along an arc of a circle there are two ways to get to the same location, a positive direction and a negative direction.

Equivalent Rotations For the rotations below. Give an equivalent rotation. 1. 90° 2. 245° 3. -180° 4. -160° Are there other angles that are equivalent?

Co-terminal Angles Co-terminal angles are angles in standard position (angles with the initial side on the positive x-axis) that have a common terminal side.

Co-terminal Angles Co-terminal angles can be calculated using the formula, Co-terminal Angle = Initial Angle + 360 n Where n is an integer.

Co-terminal Angles Find more co-terminal angles of 60°

Applying Rotations We can use some tricks to rotate figures 90°, 180°, and 270° about the origin. Use the tricks to find the new coordinates and plot.

Rotation Tricks Rotation of 90° or -____ ° about the origin can be described as (x, y) (-y, x)

Rotation Tricks Rotation of 270° or -____ ° about the origin can be described as (x, y) (y, -x)

Rotation Tricks Rotation of 180° about the origin can be described as (x, y) (-x, -y)

Example A quadrilateral has vertices A(-2, 0), B(-3, 2), C( -2, 4), and D(-1, 2). Give the vertices of the image after the described rotations. 1. RO, 180° 2. RO, 90° 3. RO, 270°

Example A triangle has vertices F(-3, 3), G(1, 3), and H(1, 1). Give the vertices of the image after the described rotations. 1. RO, 180° 2. RO, -90° 3. RO, -270°

Isometric Properties Because a rotation is an isometric transformation the following properties are preserved between the pre-image and its image: • Distance (lengths of segments are the same) • Angle measure (angles stay the same) • Parallelism (things that were parallel are still parallel) • Collinearity (points on a line, remain on the line)

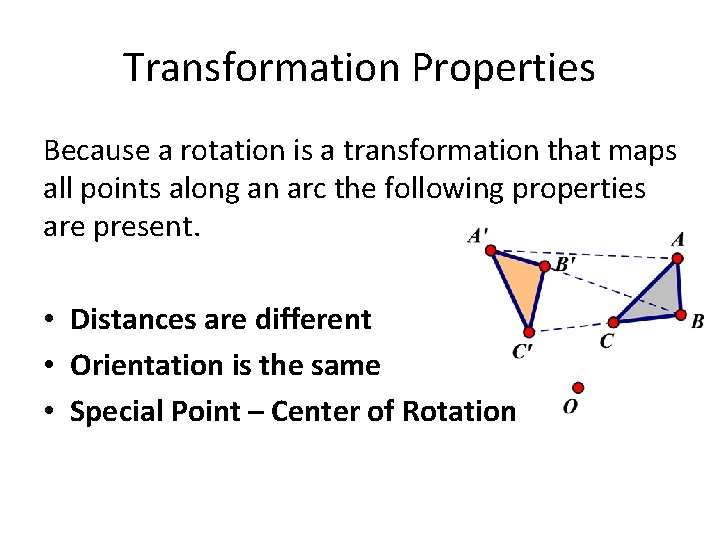
Transformation Properties Because a rotation is a transformation that maps all points along an arc the following properties are present. • Distances are different • Orientation is the same • Special Point – Center of Rotation
 Calculating specific rotation from observed rotation
Calculating specific rotation from observed rotation Types of transformations
Types of transformations Orthographic projection
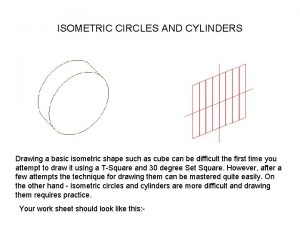
Orthographic projection Cylinder isometric view
Cylinder isometric view Isometric drawing definition geometry
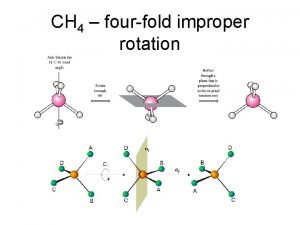
Isometric drawing definition geometry Electron geometry and molecular geometry
Electron geometry and molecular geometry 4 electron domains 2 lone pairs
4 electron domains 2 lone pairs Bonding theories
Bonding theories Rotations on the coordinate plane
Rotations on the coordinate plane Permutation volleyball
Permutation volleyball Reflections and translations
Reflections and translations Rotations quiz
Rotations quiz Trig identities from reflections and rotations
Trig identities from reflections and rotations Lesson 3 rotations
Lesson 3 rotations Cnh point group
Cnh point group Rules for rotations
Rules for rotations Revolution vs rotation
Revolution vs rotation Translations reflections and rotations
Translations reflections and rotations Lesson 14 more on the angles of a triangle
Lesson 14 more on the angles of a triangle Write a rule to describe each transformation
Write a rule to describe each transformation Translation reflection rotation
Translation reflection rotation 9-3 rotations
9-3 rotations 9.3 rotations
9.3 rotations