Retiming Definitions Retiming is a mapping from a

Retiming

Definitions • Retiming is a mapping from a given DFG, G to a retimed DFT, Gr such that the corresponding transfer function of G and Gr differ by a pure delay z-L. • Purposes – To facilitate pipelining to reduce clock cycle time – To reduce number of registers needed. (C) 2004 -2006 by Yu Hen Hu

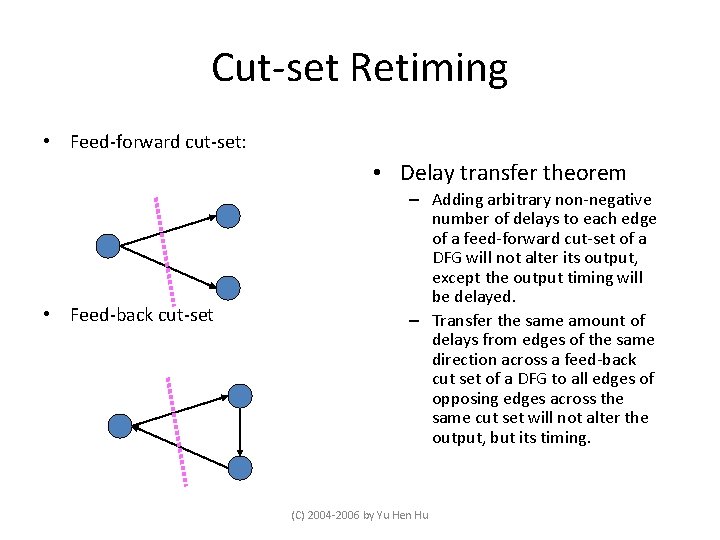
Cut-set Retiming • Feed-forward cut-set: • Delay transfer theorem • Feed-back cut-set – Adding arbitrary non-negative number of delays to each edge of a feed-forward cut-set of a DFG will not alter its output, except the output timing will be delayed. – Transfer the same amount of delays from edges of the same direction across a feed-back cut set of a DFG to all edges of opposing edges across the same cut set will not alter the output, but its timing. (C) 2004 -2006 by Yu Hen Hu

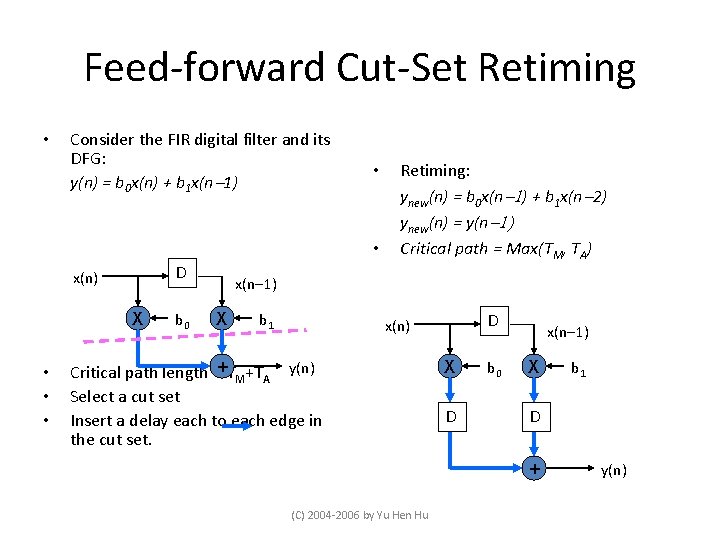
Feed-forward Cut-Set Retiming • Consider the FIR digital filter and its DFG: y(n) = b 0 x(n) + b 1 x(n-1) • • D x(n) X • • • b 0 Retiming: ynew(n) = b 0 x(n-1) + b 1 x(n-2) ynew(n) = y(n-1) Critical path = Max(TM, TA) x(n-1) X b 1 D x(n) Critical path length =+TM+TA y(n) Select a cut set Insert a delay each to each edge in the cut set. X D b 0 x(n-1) X D + (C) 2004 -2006 by Yu Hen Hu b 1 y(n)

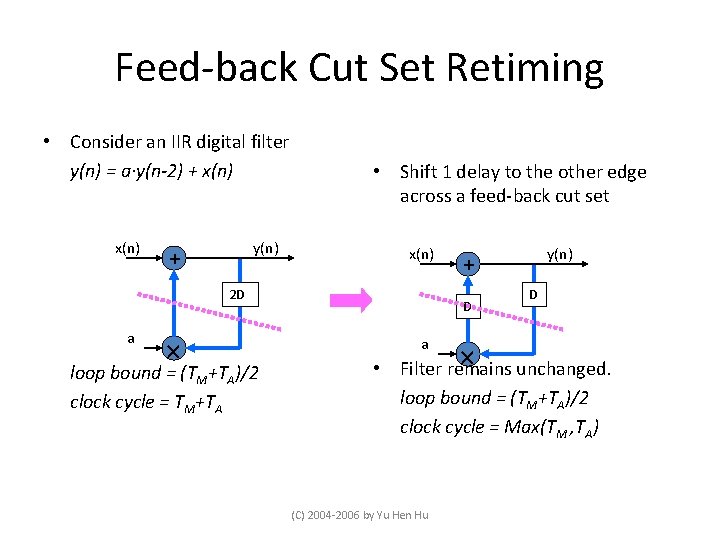
Feed-back Cut Set Retiming • Consider an IIR digital filter y(n) = a·y(n-2) + x(n) y(n) + • Shift 1 delay to the other edge across a feed-back cut set x(n) 2 D a loop bound = (TM+TA)/2 clock cycle = TM+TA D a y(n) + D • Filter remains unchanged. loop bound = (TM+TA)/2 clock cycle = Max(TM , TA) (C) 2004 -2006 by Yu Hen Hu

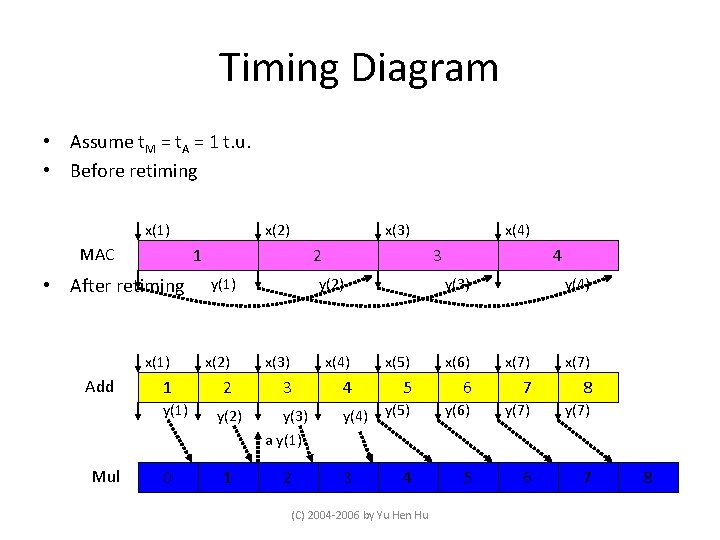
Timing Diagram • Assume t. M = t. A = 1 t. u. • Before retiming x(1) MAC 2 y(1) x(4) 3 y(2) 4 y(3) y(4) x(1) x(2) x(3) x(4) x(5) x(6) x(7) 1 2 3 4 5 6 7 8 y(2) y(3) a y(1) y(5) y(6) y(7) 1 2 4 5 6 7 y(1) Mul x(3) 1 • After retiming Add x(2) 0 y(4) 3 (C) 2004 -2006 by Yu Hen Hu 8

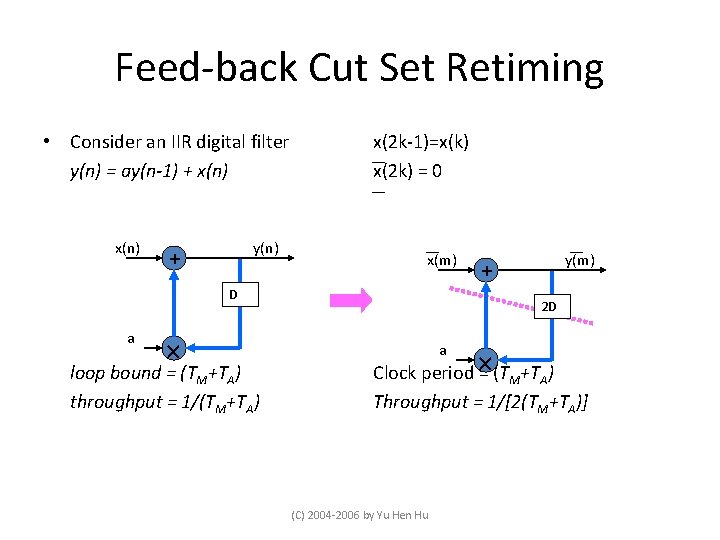
Feed-back Cut Set Retiming • Consider an IIR digital filter y(n) = ay(n-1) + x(n) y(n) + x(2 k-1)=x(k) x(2 k) = 0 x(m) D a loop bound = (TM+TA) throughput = 1/(TM+TA) y(m) + 2 D a Clock period = (TM+TA) Throughput = 1/[2(TM+TA)] (C) 2004 -2006 by Yu Hen Hu

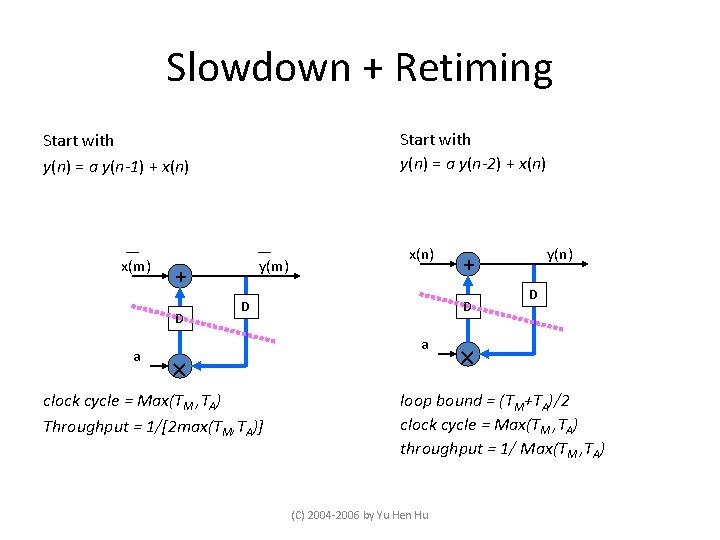
Slowdown + Retiming Start with y(n) = a y(n-2) + x(n) Start with y(n) = a y(n-1) + x(n) x(m) + D a y(m) x(n) D clock cycle = Max(TM , TA) Throughput = 1/[2 max(TM, TA)] D a y(n) + D loop bound = (TM+TA)/2 clock cycle = Max(TM , TA) throughput = 1/ Max(TM , TA) (C) 2004 -2006 by Yu Hen Hu

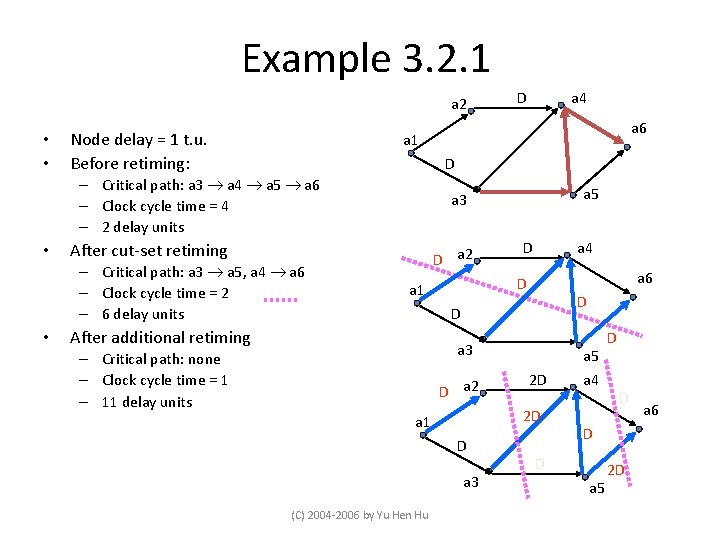
Example 3. 2. 1 a 2 • • Node delay = 1 t. u. Before retiming: a 6 D a 5 a 3 After cut-set retiming – Critical path: a 3 a 5, a 4 a 6 – Clock cycle time = 2 – 6 delay units • a 4 a 1 – Critical path: a 3 a 4 a 5 a 6 – Clock cycle time = 4 – 2 delay units • D D a 2 D a 4 a 6 D a 1 D D After additional retiming a 3 – Critical path: none – Clock cycle time = 1 – 11 delay units D a 2 2 D 2 D a 1 D a 3 (C) 2004 -2006 by Yu Hen Hu a 5 a 4 D D a 5 2 D a 6

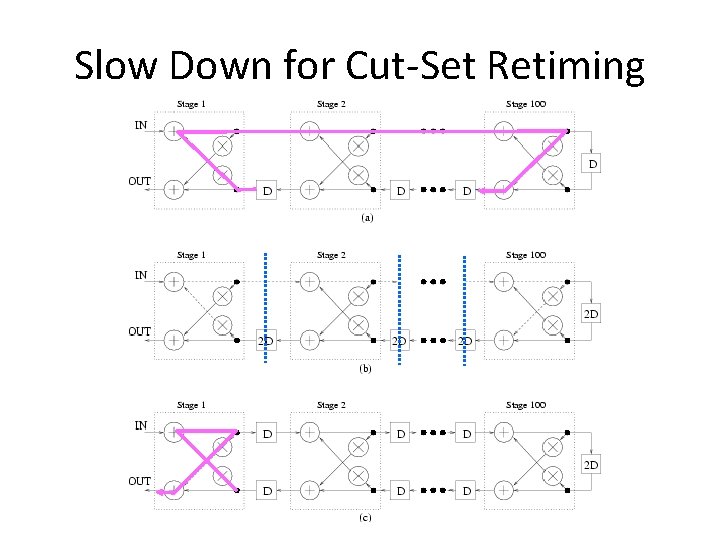
Slow Down for Cut-Set Retiming (C) 2004 -2006 by Yu Hen Hu

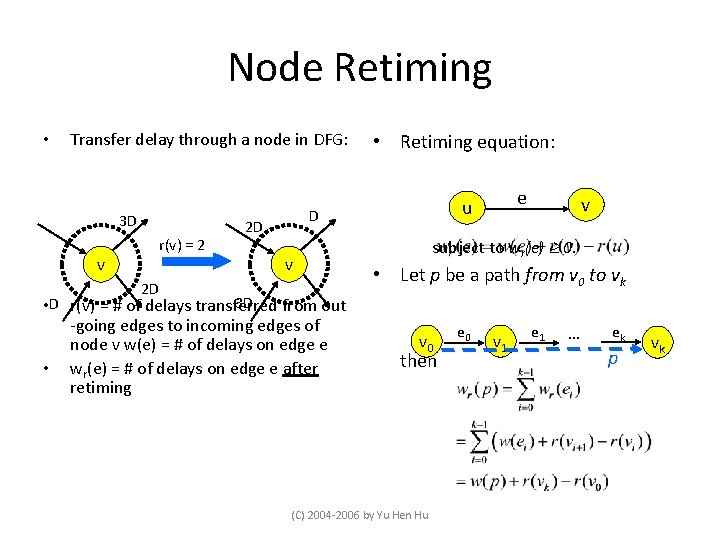
Node Retiming • Transfer delay through a node in DFG: 3 D r(v) = 2 v 2 D • Retiming equation: D 2 D v 3 D • D r(v) = # of delays transferred from out -going edges to incoming edges of node v w(e) = # of delays on edge e • wr(e) = # of delays on edge e after retiming e u v subject to wr(e) 0. • Let p be a path from v 0 to vk v 0 then (C) 2004 -2006 by Yu Hen Hu e 0 v 1 e 1 … ek p vk

Invariant Properties 1. Retiming does NOT change the total number of delays for each cycle. 2. Retiming does not change loop bound or iteration bound of the DFG 3. If the retiming values of every node v in a DFG G are added to a constant integer j, the retimed graph Gr will not be affected. That is, the weights (# of delays) of the retimed graph will remain the same. (C) 2004 -2006 by Yu Hen Hu

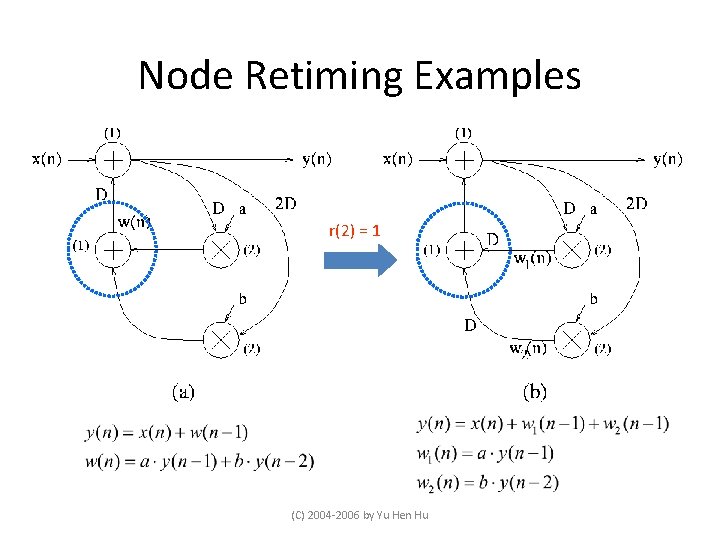
Node Retiming Examples r(2) = 1 (C) 2004 -2006 by Yu Hen Hu

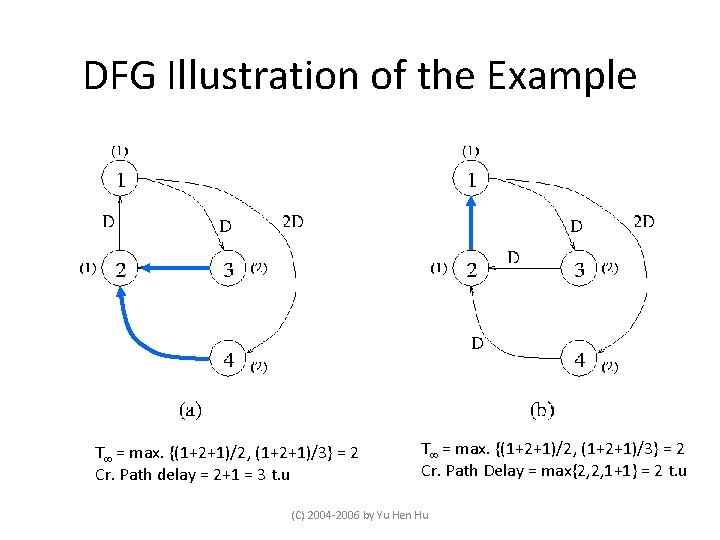
DFG Illustration of the Example T = max. {(1+2+1)/2, (1+2+1)/3} = 2 Cr. Path delay = 2+1 = 3 t. u T = max. {(1+2+1)/2, (1+2+1)/3} = 2 Cr. Path Delay = max{2, 2, 1+1} = 2 t. u (C) 2004 -2006 by Yu Hen Hu

Retiming for Minimizing Clock Period • Note that retiming will NOT alter iteration bound T. • Iteration bound is theoretical minimum clock period to execute the algorithm. • Let edge e connect node u to node v. If the node computing time t(u) + t(v) > T , then clock period T > T. For such an edge, we require that • To generalize, for any path from v 0 to vk, we have • In other words, for any possible critical path in the DFG that is larger than T , we require wr(e) 1. (C) 2004 -2006 by Yu Hen Hu

Retiming Example Revisited wr(e 21) 0, since t(2)+t(1) = 2 = T. wr(e 13) 1, since t(1)+t(3) = 3 > T. wr(e 14) 1, since t(1)+t(4) = 3 > T. wr(e 32) 1, since t(3)+t(2) = 3 > T. wr(e 42) 1, since t(4)+t(2) = 3 > T. Use eq. wr(euv) = w(e) + r(v) – r(u), w(e 21) + r(1) – r(2) = 1 + r(1) – r(2) 0 w(e 13) + r(3) – r(1) = 1 + r(3) – r(1) 1 w(e 14) + r(4) – r(1) = 2 + r(4) – r(1) 1 w(e 32) + r(2) – r(3) = 0 + r(2) – r(3) 1 w(e 42) + r(2) – r(4) = 0 + r(2) – r(4) 1 (C) 2004 -2006 by Yu Hen Hu

Solution continues • Since the retimed graph Gr remain the same if all node one must have r(2) = +1. retiming values are added by the • This implies r(3) 0. But we also same constant. We thus can set have r(3) 0. Hence r(3)=0. r(1) = 0. • These leave – 1 r(4) 0. • The inequalities become • Hence the two sets of solutions 1 – r(2) 0 or r(2) 1 are: 1 + r(3) 1 or r(3) 0 r(0) = r(3) = 0, r(2) = +1, and r(4) = 2 + r(4) 1 or r(4) – 1 0 or -1. r(2) – r(3) 1 or r(3) r(2) - 1 r(2) – r(4) 1 or r(2) r(4) + 1 (C) 2004 -2006 by Yu Hen Hu

Systematic Solutions Given a systems of inequalities: r(i) – r(j) k; 1 i, j N Construct a constraint graph: 1. Map each r(i) to node i. Add a node N+1. 2. For each inequality r(i) – r(j) k, draw an edge eji such that w(eji) = k. 1. Draw N edges e. N+1, i = 0. a) The system of inequalities has a solution if and only if the constraint graph contains no negative cycles b) If a solution exists, one solution is where ri is the minimum length path from the node N+1 to the node i. Shortest path algorithms: (Applendix A) Bellman-Ford algorithm Floyd-Warshall algorithm (C) 2004 -2006 by Yu Hen Hu

Bellman-Ford Algorithm Find shortest path from an arbitrarily chosen origin node U to each node in a directed graphif no negative cycle exists. Given a direct graph w(m, n): weight on edge from node m to node n, = if there is no edge from m to n r(i, j): the shortest path from node U to node i within j-1 steps. r(i, 1) = w(U, i), r(i, j+1) = min {r(k, j) + w(k, i)}, -3 1 1 2 1 1 4 2 3 j = 1, 2, …, N-1 if max(r(: , n-1)-r(: , n))>0, then there is a negative cycle. Else, r(i, n-1) gives shortest cycle length from i to U. Note that 1 > 0, hence there is at least one negative cycle. (C) 2004 -2006 by Yu Hen Hu spbf. m

Floyd-Warshall Algorithm Find shortest path between all possible pairs of nodes in the graph provided no negative cycle exists. Algorithm: Initialization: R(1) =W; For k=1 to N R(k+1)(u, v) = min{R(k)(u, : ) + R(k)(: , v)} If R(k)(u, u) < 0 for any k, u, then a negative cycle exist. Else, R(N+1)(u, v) is SP from u to v (C) 2004 -2006 by Yu Hen Hu -3 1 1 2 4 2 3

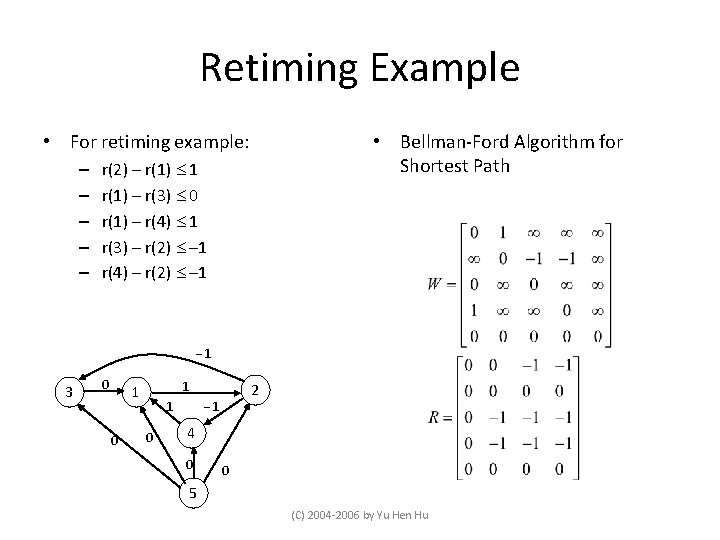
Retiming Example • For retiming example: – – – • Bellman-Ford Algorithm for Shortest Path r(2) – r(1) 1 r(1) – r(3) 0 r(1) – r(4) 1 r(3) – r(2) – 1 r(4) – r(2) – 1 -1 3 0 1 1 0 -1 1 0 2 4 0 0 5 (C) 2004 -2006 by Yu Hen Hu

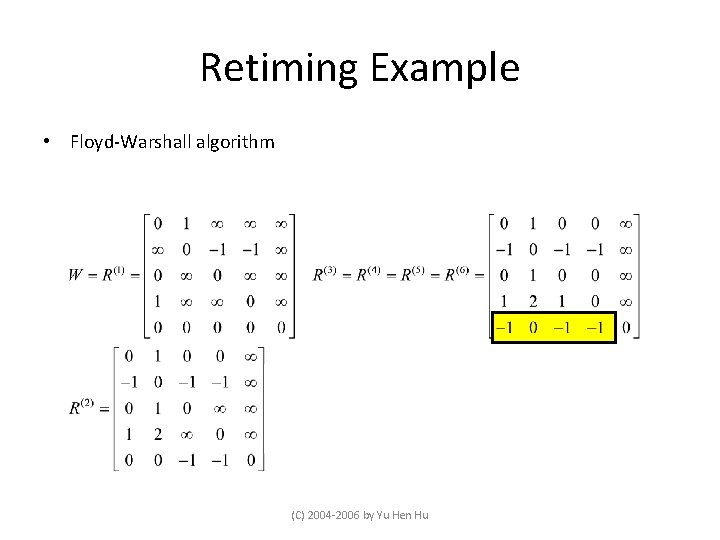
Retiming Example • Floyd-Warshall algorithm (C) 2004 -2006 by Yu Hen Hu

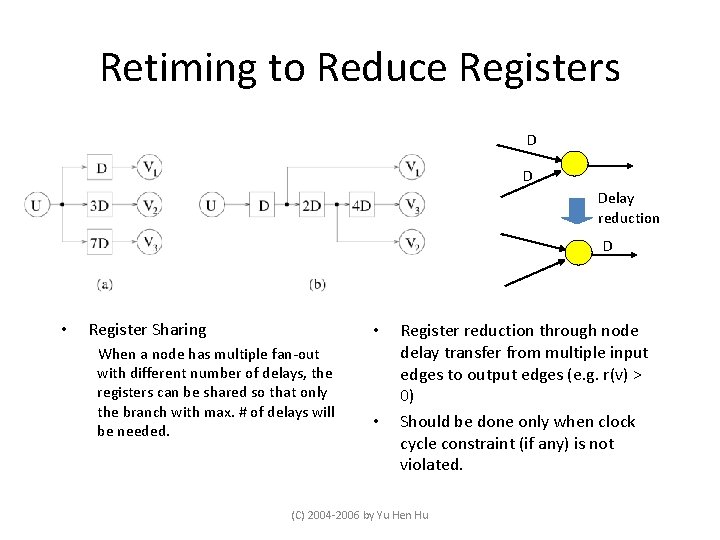
Retiming to Reduce Registers D D Delay reduction D • Register Sharing • When a node has multiple fan-out with different number of delays, the registers can be shared so that only the branch with max. # of delays will be needed. • Register reduction through node delay transfer from multiple input edges to output edges (e. g. r(v) > 0) Should be done only when clock cycle constraint (if any) is not violated. (C) 2004 -2006 by Yu Hen Hu

Time Scaling (Slow Down) • Transform each delay element … x(3) x(2) x(1) (register) D to ND and reduce the sample frequency by N fold will slow down the computation N times. • During slow down, the processor clock cycle time remains unchanged. Only the sampling … -- x(3) -- x(2) -- x(1) cycle time increased. • Provides opportunity for retiming, and interleaving. + y(2) y(1) D + … y(3) -- y(2) -- y(1) 2 D (C) 2004 -2006 by Yu Hen Hu … y(3)