Reductions Complexity D Moshkovitz 1 Motivation Reductions are

Reductions Complexity ©D. Moshkovitz 1

Motivation • Reductions are our main tool for comparison between problems. Complexity ©D. Moshkovitz 2

Introduction • Objectives: – To formalize the notion of “reductions”. • Overview: – – – Complexity ©D. Moshkovitz Karp reductions HAMPATH p HAMCYCLE Closeness under reductions Cook reductions Completeness 3

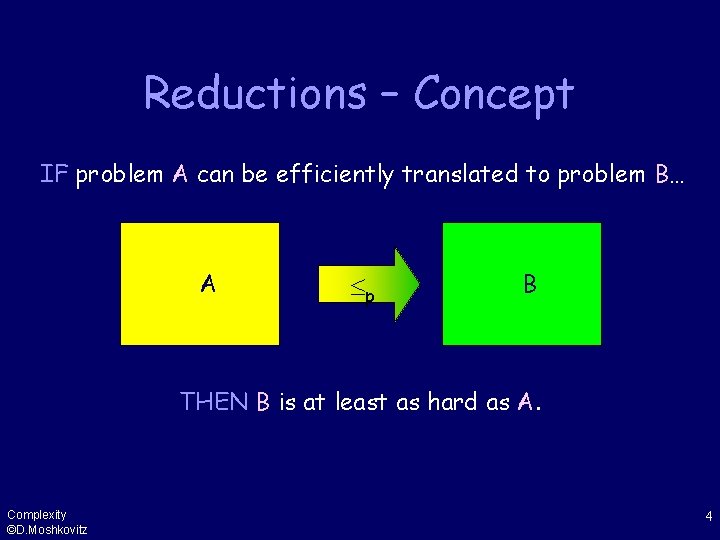
Reductions – Concept IF problem A can be efficiently translated to problem B… A p B THEN B is at least as hard as A. Complexity ©D. Moshkovitz 4

SIP 250 Reductions – Formal I. e – there exists a polynomial time TM which Definition halts with f(w) on its tape when given input w. Definition: Language A is polynomial time reducible to language B if… a polynomial time computable function f: * * exists, Denote A p B where for every w, w A f(w) B f is referred to as a polynomial-time reduction of A to B. Complexity ©D. Moshkovitz 5

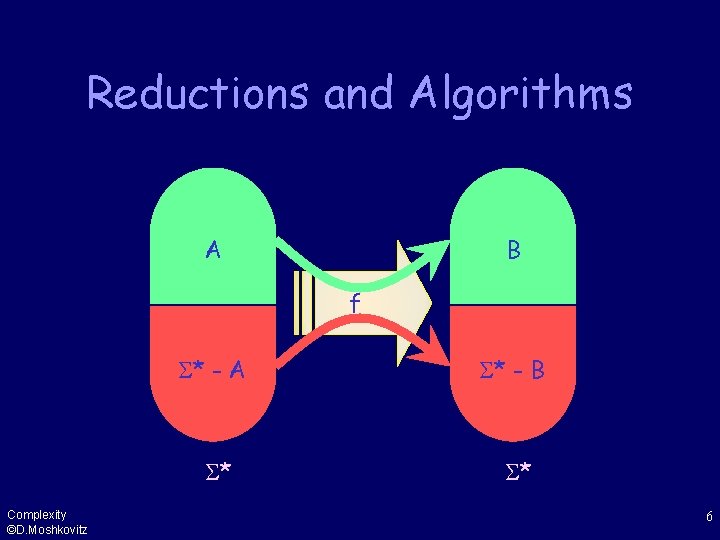
Reductions and Algorithms A B f Complexity ©D. Moshkovitz * - A * - B * * 6

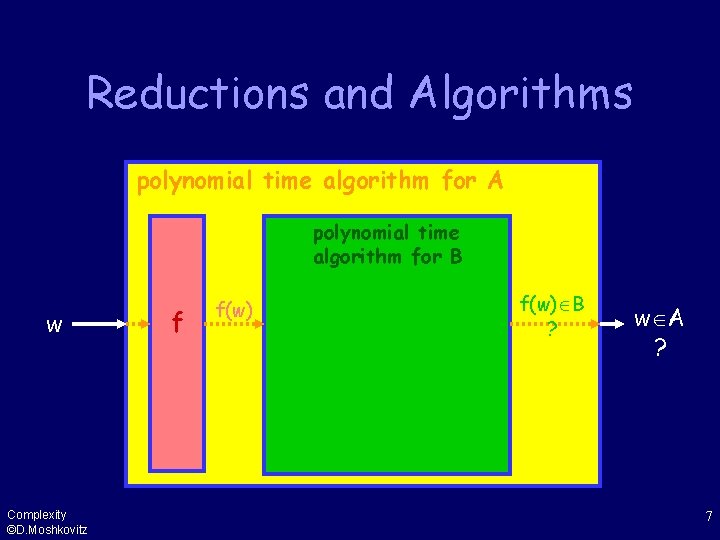
Reductions and Algorithms polynomial time algorithm for A polynomial time algorithm for B w Complexity ©D. Moshkovitz f f(w) B ? w A ? 7

How to Reduce? 1. Construct f. 2. Show f is polynomial time computable. 3. Prove f is a reduction, i. e show: 1. If w A then f(w) B 2. If f(w) B then w A Complexity ©D. Moshkovitz 8

Terminology • The type of reductions we’ve just described is also called: – Polynomial-time mapping reduction – Polynomial-time many-one reduction – Polynomial-time Karp reduction • We’ll always refer to such reductions unless otherwise specified. Complexity ©D. Moshkovitz 9

Example • To demonstrate a reduction, we’ll revisit the example we gave in the introduction. • We’ll rephrase and formalize the seating and tour problems • And demonstrate a slightly different reduction between them. Complexity ©D. Moshkovitz 10

Hamiltonian Path Instance: a directed graph G=(V, E) and two vertices s t V. Problem: To decide if there exists a path from s to t, which goes through each node once. In the version presented in the introduction we asked for some path, without specifying the start and end vertices. Complexity ©D. Moshkovitz 11

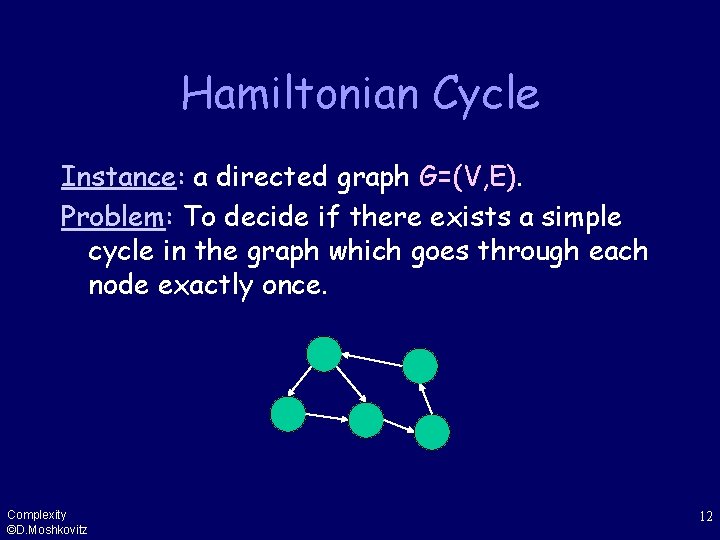
Hamiltonian Cycle Instance: a directed graph G=(V, E). Problem: To decide if there exists a simple cycle in the graph which goes through each node exactly once. Complexity ©D. Moshkovitz 12

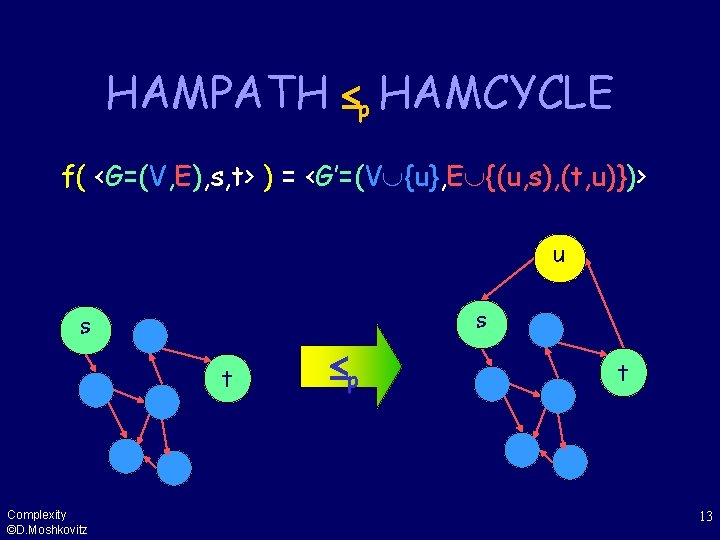
HAMPATH p HAMCYCLE f( <G=(V, E), s, t> ) = <G’=(V {u}, E {(u, s), (t, u)})> n s s t Complexity ©D. Moshkovitz p t 13

Correctness • (Completeness) If there exists a Hamiltonian path (v 0=s, v 1, …, vn=t) in the original graph, then (u, v 0=s, v 1, …, vn=t, u) is a Hamiltonian cycle in the new graph. Complexity ©D. Moshkovitz 14

Correctness • (Soundness) (u, s) and (t, u) must be in any Hamiltonian cycle in the constructed graph, thus removing u yields a Hamiltonian path from s to t. Complexity ©D. Moshkovitz 15

How to Reduce? 1. Construct f. easy to 2. Show f is polynomial time computable. verify 3. Prove f is a reduction, i. e show: 1. If w HAMPATH then f(w) HAMCYCLE 2. If f(w) HAMCYCLE then w HAMPATH Complexity ©D. Moshkovitz 16

Closeness Under Reductions Definition: A complexity class C is closed under reductions if, whenever L is reducible to L’ and L’ C, then L is also in C. L’ C L Complexity ©D. Moshkovitz 17

Observation Theorem: P, NP, PSPACE and EXPTIME are closed under polynomial-time Karp reductions. Proof: Filling in the exact details is left to the reader. (See sketch) Complexity ©D. Moshkovitz 18

Other Types of Reductions • Cook Reduction: Use an efficient “black box” (procedure) that decides B, to construct a polynomial-time machine which decides A. polynomial time algorithm for B polynomial time algorithm for A Complexity ©D. Moshkovitz 21

Cook reduction of HAMCYCLE to HAMPATH. • For each edge (u, v) E, – if there’s a Hamiltonian path from v to u in the graph where (u, v) is removed, output ‘YES’, exit • Output ‘NO’ Make sure it’s efficient! Complexity ©D. Moshkovitz HAMPATH oracle 22

How do Cook and Karp Reductions Differ? • Cook reductions allow us to call the procedure many times (instead of 1). • When Karp reducing, we must output the answer of the procedure. Complexity ©D. Moshkovitz 23

On the Relation Between Cook and Karp Reductions • Observation: Karp reductions are special cases of Cook reductions. Complexity ©D. Moshkovitz 24

Food for Thought… • Which complexity classes are closed under Cook reductions? Complexity ©D. Moshkovitz 25

Completeness Definition: Let C be a complexity class and let L be a language. We say L is C-Complete if: 1. L is in C 2. For every language A C, A is reducible to L. Complexity ©D. Moshkovitz 26

C-Complete Languages hardness C-Complete C Complexity ©D. Moshkovitz 27

Observation Theorem: If two classes C and C’ are both closed under reductions (of some specific type) and there is a language L which is complete for both C and C’, then C=C’. Proof: W. l. o. g we’ll only show C C’. All languages in C are reducible to L. Since C’ is closed under reductions, it follows that C C’. Complexity ©D. Moshkovitz 28

Corollary If any NP-Complete problem is in P, then P=NP. Complexity ©D. Moshkovitz 29

Summary • In this lecture we’ve introduced many types of reductions: – Cook/Karp reductions – Polynomial-time reductions • We’ve defined the notion of completeness • And seen how it can help us prove equality of complexity classes. • Nevertheless, we are still not convinced complete languages even exist. Complexity ©D. Moshkovitz 30