Recursion 128 Introduction to Recursion Recursive procedures are

Recursion 1/28

Introduction to Recursion Recursive procedures are functions that invoke themselves either directly (call themselves from within themselves) or indirectly (calls another method that calls original method. ) Recursion: . An alternative to iteration. Recursion can be very elegant at times, . Not inexpensive to implement. . . Classic examples of recursion. Recursive calculation of a string length, factorials, divide and conquer, towers of Hanoi, binary searches, and more Recursive functions are used in many applied areas. . In artificial intelligence. . In searching data structures that are themselves "recursive" in nature, such as trees. Concepts and implementation of recursive functions is an important topic. 2/28

Consider: Want to sum the numbers from 1 to 5 int public sum (int n) { if (n <= 1) return n; else return (n + sum(n-1)); }// end sum() Base case Recursive Case Looks pretty simple… Notice the recursion in the Else branch Note the ‘return’ calls itself! (calls the method it resides in!) Note the ‘Base Case’ Note the ‘Recursive Case’ Note the return instruction is not ‘satisfied’ until it can totally execute, that is, the machine can add n + the sum (n-1)! Let’s look how this is executed! 3/28

int public sum (int n) { if (n <= 1) return n; else return (n + sum(n-1)); }// end sum() START WITH N = 5: Look at return statement. We get a VALUE (5) plus a (recursive) ‘CALL: ’ Thus the return is not “satisfied” because the call is not complete. equivalently, the return statement doesn’t have all the values. Results of the ‘return’ are suspended until we have a value for sum(n-1). But the call it ‘itself’ is initiated to get a value for sum(n-1). Thus: SUM(5): 5 + SUM(4) - A FUNCTION CALL (SUM(4)) WHOSE VALUE WE AWAIT So what does the ‘next’ call look like? SUM(4): 4 +SUM(3) -A FUNCTION CALL WHOSE VALUE WE AWAIT SUM(3): 3 + SUM(2) -A FUNCTION CALL WHOSE VALUE WE AWAIT SUM(2): 2 + SUM(1) - A FUNCTION CALL WHOSE VALUE WE AWAIT 4/28 SUM(1): 1

IT IS ONLY WHEN WE GET THE VALUE FOR SUM(1) = 1 (reached the base case, where we have a discrete value is assigned and execution of the instruction is complete) THAT WE CAN GO "BACK UP" (one call at a time) THROUGH THE SUSPENDED FUNCTION CALLS AND CALCULATE THEIR VALUES AND THUS "COMPLETE THAT ORIGINAL CALL". . . We need to ‘satisfy’ a particular function call before we can proceed up the calling sequence chain. Note this notion of ‘completing’ the call; that is, satisfying the call…. 5/28

WHEN WE GET SUM(1)=1, THEN WE REFER TO 2 + SUM(1) equals 2 + 1 = 3. (complete) WE NOW HAVE A VALUE FOR SUM(2). The call: SUM(2) is satisfied!! NEXT, GOING UP THE SUSPENDED CALLS. . SUM (3) = 3+SUM(2), which is 3 + 3 OR 6; (now complete) We now have a value for SUM(3) The call: SUM(3) is ‘satisfied. ’ Proceed upward. NEXT, SUM (4) = 4+SUM(3), WHICH IS 4 + 6 OR 10; (now complete) FINALLY, SUM (5) = 5+SUM(4), WHICH IS 5 + 10 OR 15 (now complete) ALL THESE PREVIOUS FUNCTION CALLS ARE "PENDING" OR "INCOMPLETE" PENDING A RETURNED VALUE FROM THE CALLED FUNCTION, which was part of the return statement. 6/28

The Expense of Recursive Functions. RECURSION => has a significant overhead…. "DEEPER" WE GO => Need ADDITIONAL COPIES OF THE DATA. . NOT ALWAYS SMALL NUMBER OF DATA ITEMS. . These ‘copies’ are stored in "STACK FRAMES“ which contain current values and outstanding function calls, and more (to be discussed). Each "CALL" results in a STACK FRAME. Each requires space, allocation of space, and processing time. NOTE: . . Recursive Functions – Not efficient from a System Resource perspective. . . Can pay dividends in: . . . Ease of writing and maintaining as compared to the writing of iterative procedures. (You will see in trees. ). . Termed ‘elegant’ by some 7/28

Notion of the Base Case and Recursive Case Procedure: 1. Find a "Base Case " (That is what we shoot for. ) 2. Develop the Recursive Case: Base Case was sum(1). We know the answer to this one! we will always have a simple *normally’ assignment statement here, such as assigning a value of null or 0 or 1. You will see. Recursive Case was sum (n-1) which will (must) eventually lead to sum(1) Your general recursive case must progress to the base case. An absolute MUST to conclude the method calls. 8/28

Consider: FACTORIAL FUNCTION Where n! = n* (n-1) * (n-2) *. . . 1! * 0! Where 1! = 1 & 0! = 1 by definition. Thus 5! = 5 * 4 * 3 * 2 * 1 = 120 9/28

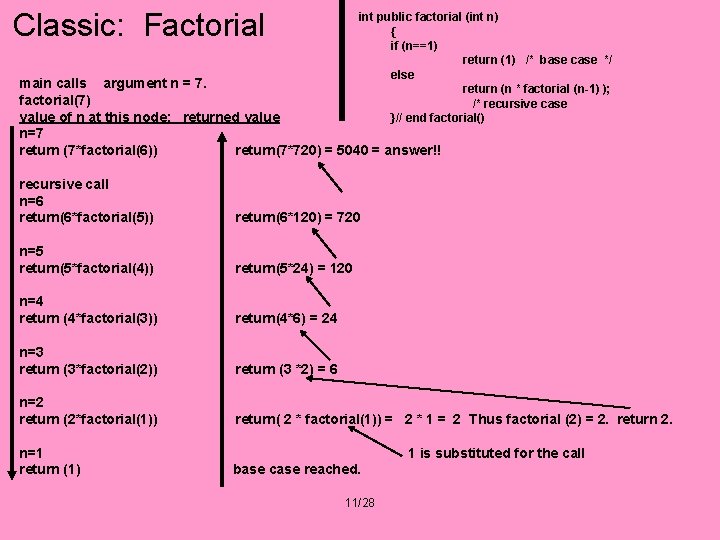
Classic: Factorial RECURSIVE FUNCTION IS WRITTEN AS: int public factorial (int n) { if (n==1) return (1) /* THIS IS THE BASE CASE */ else return (n * factorial (n-1) ); /* RECURSIVE CASE */ }end factorial () RECALL: When a function calls itself, this implies development of a new set of local variables. . Same “variable names” but very different variables (different memory addresses) and different values! There may also be some other temporary variables during the life of a particular ‘call. ’ 10/28 OK, so how does this work?

Classic: Factorial int public factorial (int n) { if (n==1) return (1) /* base case */ else return (n * factorial (n-1) ); /* recursive case }// end factorial() main calls argument n = 7. factorial(7) value of n at this node: returned value n=7 return (7*factorial(6)) return(7*720) = 5040 = answer!! recursive call n=6 return(6*factorial(5)) return(6*120) = 720 n=5 return(5*factorial(4)) return(5*24) = 120 n=4 return (4*factorial(3)) return(4*6) = 24 n=3 return (3*factorial(2)) return (3 *2) = 6 n=2 return (2*factorial(1)) return( 2 * factorial(1)) = 2 * 1 = 2 Thus factorial (2) = 2. return 2. n=1 return (1) 1 is substituted for the call base case reached. 11/28

Base Case "Base case" a very important notion! A base case is one that is simple; one that we are working ‘down’ toward working "down" toward, since, as it turns out, we normally go "down" or “decrease” some value or some quantity (such as length of a string) toward the base case. (e. g. We know the length of an empty string is 0; we know that 0! And 1! By definition = 1…) Determining the base case ensures the recursive function will terminate someday!! 12/28

Writing Recursive Programs. Have spoken about the "base case" and "recursive case. " Difficulty in writing recursive routines is identifying. . base case, and (Some books calls this: "trivial case“). . Recursive case. ( Some books calls this: "complex case") Base case A case that is not recursive and directly obtainable. Will have a value of 1 or 0 or null or something having some kind of discrete value… Recursive case A case that is ultimately defined in terms of base case. 13/28

Stated equivalently: Complex case. Must be defined in terms of a "simpler" case. Plus the base case must be: . a directly solvable, non-recursive trivial case We develop solutions using the assumption that the simpler case has already been solved. 14/28

Example: Write a recursive routine that computes a*b Now, what do we know? When b = 1, case is trivial, because a*b = a. TRIVIAL CASE So, in general, then, a*b may be defined in terms of a*(b-1) with definition: a*b = a*(b -1) + a right? ? Certainly 5*4 = 5*3 + 5 = 20. Here, recursion is based on the second parameter, b, alone. Can you write such a recursive routine from this knowledge? YES! 15/28

me: ) So, how about: int public mult (int a, int b) { Easy to see: if (b == 1) return a; else We can say: return (a + mult(a, b-1)); } // end mult() Agree with this? 16/28

me: ) int public mult (int a, int b) { if (b == 1) return a; else return (a + mult(a, b-1)); } Does this work? Let a * b <==> 4 * 3 (that is, a is 4, b is 3). So, (brute force approach) main: call mult(4, 3). . (see above) 1. Executing the code: if (b == 1) ? No it does not; b = 3, so we cannot ‘return a’ We must: return (4 + mult(4, 2)); Thus the return statement is suspended… 2. Let’s execute the method again… if (b == 1) ? no. b = 2. and so: hold on to 4 and call method again as in: else return (4 + mult (4, 1)); once again, the return is suspended 3. Let’s execute the method again… if (b == 1) Alas! yes. return a => return 4. (this call – mult (4, 1) - is satisfied. . ) Next slide… 17/28

me: ) int public mult (int a, int b) { if (b == 1) return a; else return (a + mult(a, b-1)); } So, (See 2) we have return 4 + mult(4, 1) and mult(4, 1) yields a 4 Thus, 4 + mult(4, 1) = 4 + 4 = 8 and THIS call is "satisfied" 8 is returned for mult(4, 2) And See 1. we have return 4 + mult (4, 2) and mult (4, 2) call returned an 8. Thus, 4 + mult(4, 2) = 4 + 8 = 12. and THIS call is "satisfied" 12 is returned to main - the call mult (4, 3) = 12 18/28

SIMULATING RECURSION Some languages do not support recursion. It is often very common to be able to come up with a recursive solutions to a problem. Since some compilers do not support recursion, we need to be able to come up with non-recursive solutions. (Iterative Routines) Recursive solutions are often more expensive than non-recursive solutions in Time and space. Authors assert: a small price to pay for logical simplicity and selfdocumentation of recursive solutions. Heavy use of recursive solutions for production systems may dictate non-recursive solutions to problems. Let's look at iterative solutions first. 19/28

CONSIDER: CALL: rout(x); FUNCTION: rout (int a) //here, nothing is specified as return type. x is the ‘argument’ (sometimes called ‘actual parameter’) a is the ‘formal parameter. ’ When we call a function: 1. Pass arguments. Values are “copied” to automatic local variable (for Call by Value) 2. Allocate and initialize local variables. Local declarations are declared at start. Any temporaries declared during execution 3. Transferring control to/from the function. Need a return address. . Function returns via a branch back. . Function stores this address in its own area. When we return from a function: 1. Retrieve return address. 2. Free up data areas. Local variables, argument information, temporaries and return address storage space. 3. Execute the branch and transfer values ‘back’ Control is returned to the statement calling the function. 20/28 Value is typically stored in a register where calling program can retrieve it.

IMPLEMENTING RECURSIVE FUNCTIONS. What more does implementation of recursive solutions require? In recursion: an entirely new data area for each particular call is allocated. Data area contains all parameters, local variables, temporary data, and a return address, as stated. The data area is not associated with the function, but with a specific call to the function (and with EACH call). Each call causes a new data area to be allocated. Each reference in the executable code is to the data of the most recent call. Return? Current data area is freed up, and the data area allocated immediately prior to current area is now ‘current. ’ All this, of course, implies a stack, just as in iterative case, where there is a stack of return addresses. 21/28

• Previews of coming distractions: – Consider an iterative approach to processing a binary tree (push and pop) • Define binary tree and a LNR traversal • a ‘tree’ is a recursive data structure… 22/28

Stacks are Used. (Stack Frames) In practice, we use a single large stack, with each element of the large stack being an entire data area containing data for a specific call. In recursive returns we may do some / all of the following: we pop the stack to get to: Returned values Returned addresses Data areas Branch to statement invoking function taken. Calling function regains control and continues for a particular ‘call’ or message invocation 23/28

EFFICIENCY OF RECURSION. Generally speaking, non-recursive versions will execute more efficiently (time / space). Why? Overhead involved in entering and exiting blocks is avoided in non-recursive solutions. Often, in iterative solutions, we have a number of local variables and temporaries that do not have to be saved and restored via a stack. But, non-recursive solutions may cause needless stacking activity (you will have to do it yourself). In recursive solutions, compiler is usually unable to identify some variables and these are therefore stacked and 24/28 unstacked to ensure there are no problems (beyond us here…)

In Practice: Conflicts • There are conflicts between – machine efficiency and – programmer efficiency • It is more efficient for the machine to lose some efficiency than a high-cost programmer. • It may not be worth the effort to construct a non-recursive solution for a problem solved naturally recursively. 25/28

Recursive routines can be as fast or faster if you can eliminate some of the stacks and when recursive versions do not contain any extra parameters and local variables that may need saving… Note: . factorial does not need a stack. . Fibonacci numbers contain unnecessary second recursive calls (and also does not need a stack). Thus, in these, recursion should be avoided. Also, Push(), pop(), Is. Empty() and tests for overflow, underflow are expensive in writing iterative routines. (You will see when we get to trees) This expense can outweigh expensive and overhead of recursion. Thus to maximize actual run-time efficiency of a non-recursive translation, these calls should be replaced by in-line code. Overflow/underflow tests can be eliminated when it is known that we are operating within array bounds. 26/28

class Binary. Search. App { public static void main(String[] args) { int max. Size = 100; // array size ord. Array arr; // reference to array arr = new ord. Array(max. Size); // create the array arr. insert(72); // insert items arr. insert(90); arr. insert(45); arr. insert(126); arr. insert(54); arr. insert(99); arr. insert(144); arr. insert(27); arr. insert(135); arr. insert(81); arr. insert(18); arr. insert(108); arr. insert(9); arr. insert(117); arr. insert(63); arr. insert(36); arr. display(); // display array int search. Key = 27; // search for item if( arr. find(search. Key) != arr. size() ) System. out. println("Found " + search. Key); else System. out. println("Can't find " + search. Key); } // end main() 27/28 } // end class Binary. Search. App

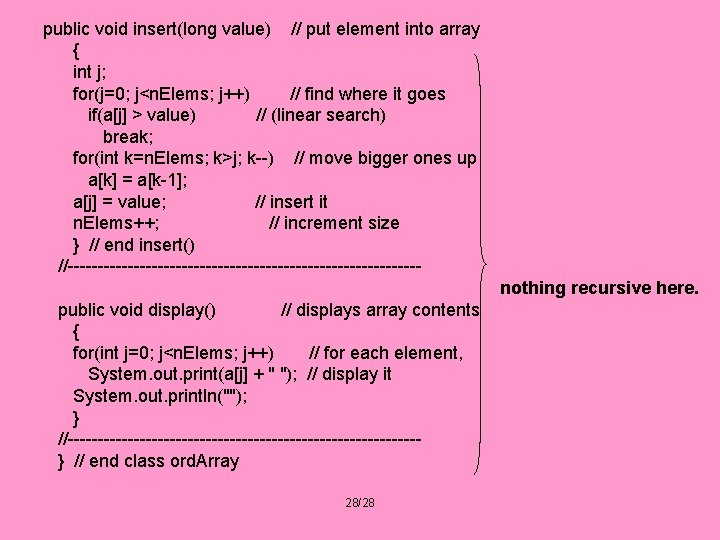
public void insert(long value) // put element into array { int j; for(j=0; j<n. Elems; j++) // find where it goes if(a[j] > value) // (linear search) break; for(int k=n. Elems; k>j; k--) // move bigger ones up a[k] = a[k-1]; a[j] = value; // insert it n. Elems++; // increment size } // end insert() //-----------------------------nothing recursive here. public void display() // displays array contents { for(int j=0; j<n. Elems; j++) // for each element, System. out. print(a[j] + " "); // display it System. out. println(""); } //-----------------------------} // end class ord. Array 28/28

// binary. Search. java class ord. Array { private long[] a; // ref to array a private int n. Elems; // number of data items //-----------------------------public ord. Array(int max) // constructor { a = new long[max]; // create array n. Elems = 0; } //-----------------------------public int size() { return n. Elems; } //-----------------------------public int find(long search. Key) { return rec. Find(search. Key, 0, n. Elems-1); } //-----------------------------private int rec. Find(long search. Key, int lower. Bound, int upper. Bound) { int cur. In; cur. In = (lower. Bound + upper. Bound ) / 2; if(a[cur. In]==search. Key) return cur. In; // found it else if(lower. Bound > upper. Bound) return n. Elems; // can't find it exception conditions (found it and not found. else // divide range { if(a[cur. In] < search. Key) // it's in upper half return rec. Find(search. Key, cur. In+1, upper. Bound); recursive call Notice how short the routine is !!!!! else // it's in lower half return rec. Find(search. Key, lower. Bound, cur. In-1); 29/28 recursive call } // end else divide range } // end rec. Find()