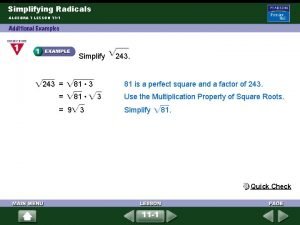
Radicals and Rational Exponents Copyright Cengage Learning All





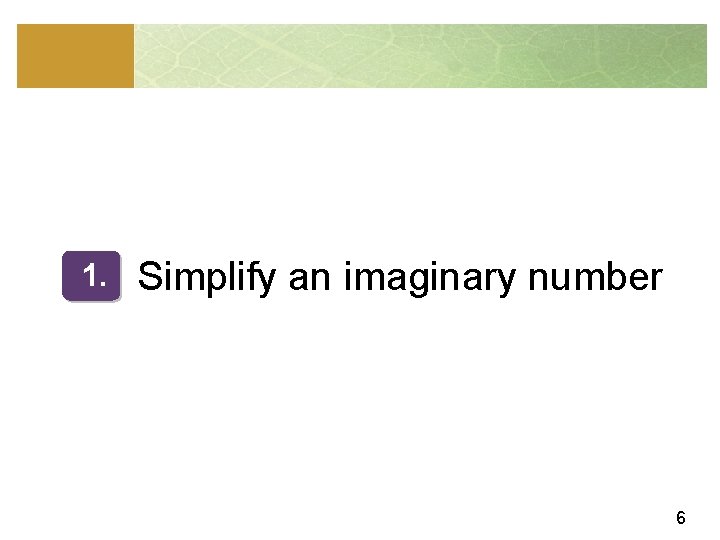






































- Slides: 44

Radicals and Rational Exponents Copyright © Cengage Learning. All rights reserved. 9

S e c tio n 9. 7 Complex Numbers Copyright © Cengage Learning. All rights reserved.

Objectives 1 Simplify an imaginary number. 2 Write a complex number in a + bi form. 3 Determine whether two complex numbers are equal. 4 Simplify an expression containing complex numbers. 3

Objectives 5 Rationalize the denominator of a fraction that contains a complex number. 6 Find a specified power of i and apply this pattern to simplifying an expression. 7 Find the absolute value of a complex number. 4

Complex Numbers We have seen that square roots of negative numbers are not real numbers. However, there is a set of numbers, called the complex numbers, in which negative numbers do have square roots. In this section, we will discuss this broader set of numbers. 5
1. Simplify an imaginary number 6

Simplify an imaginary number Consider the number. Since no real number squared is – 3, is not a real number. For years, people believed that numbers such as and were nonsense. In the 17 th century, René Descartes (1596– 1650) called them imaginary numbers. Today, imaginary numbers have many important uses, such as describing the behavior of alternating current in electronics. 7

Simplify an imaginary number The imaginary number letter i: often is denoted by the Because i represents the square root of – 1, it follows that i 2 = – 1 If we assume that multiplication of imaginary numbers is commutative and associative, then (2 i)2 = 22 i 2 = – 1 = 4(– 1) = – 4 8

Simplify an imaginary number Since (2 i)2 = – 4, 2 i is a square root of – 4, and we can write = 2 i This result also can be obtained by using the multiplication property of radicals: 9

Example 1 Simplify: a. b. Solution: We can use the multiplication property of radicals to simplify any imaginary number. For example, a. b. 10

Simplify an imaginary number Properties of Radicals If at least one of a and b is a nonnegative real number, then and ( b 0) 11

Simplify an imaginary number Comment If a and b are negative, then. We know that, the simplified form of a radical expression does not contain a negative radicand. Therefore the and the must be simplified prior to multiplying. For example, if a = – 16 and b = – 4, we have = (4 i)(2 i) = 8 i 2 = 8(– 1) = – 8 The imaginary numbers are a subset of a set of numbers called the complex numbers. 12

Simplify an imaginary number Complex Numbers A complex number is any number that can be written in the standard form a + bi, where a and b are real numbers and In the complex number a + bi, a is called the real part, and b is called the imaginary part. 13

Simplify an imaginary number If b = 0, the complex number a + bi is a real number. If b 0 and a = 0, the complex number 0 + bi (or just bi) is an imaginary number. Any imaginary number can be expressed in bi form. For example, =i 14

Simplify an imaginary number The relationship among the real numbers, the imaginary numbers, and the complex numbers is shown in Figure 9 -18 15

2. Write a complex number in a + bi form 16

Write a complex number in a + bi form The next example shows how to write complex numbers in (a + bi) form. It is common to use (a – bi) as a substitute for a + (–b)i. 17

Example 2 Write each number in a + bi form. a. 7 b. 3 i c. 4 – d. 5 + Solution: a. 7 = 7 + 0 i b. 3 i = 0 + 3 i 18

Example 2 – Solution cont’d c. = 4 – 4 i d. 19

3. Determine whether two complex numbers are equal 20

Determine whether two complex numbers are equal Equality of Complex Numbers The complex numbers a + bi and c + di are equal if and only if a=c and b=d Because of the preceding definition, complex numbers are equal when their real parts are equal and their imaginary parts are equal. 21

Example 3 a. b. c. because if and only if and and 22

4. Simplify an expression containing complex numbers 23

Simplify an expression containing complex numbers Addition and Subtraction of Complex Numbers Complex numbers are added and subtracted as if they were binomials: (a + bi) + (c + di) = (a + c) + (b + d)i (a + bi) – (c + di) = (a + bi) + (–c – di) = (a – c) + (b – d)i The preceding definition suggests that when adding or subtracting two complex numbers, we add or subtract the real parts and then add or subtract the imaginary parts. 24

Example 4 Perform the operations. a. b. 25

Example 4 cont’d c. d. 26

Simplify an expression containing complex numbers To multiply a complex number by an imaginary number, we use the distributive property to remove parentheses and simplify. For example, – 5 i(4 – 8 i) = – 5 i(4) – (– 5 i)8 i Use the distributive property to remove parentheses. = – 20 i + 40 i 2 Simplify. = – 20 i + 40(– 1) Remember that i 2 = – 1. = – 40 – 20 i 27

Simplify an expression containing complex numbers To multiply two complex numbers, we use the following definition. Multiplying Complex Numbers Complex numbers are multiplied as if they were binomials, with i 2 = – 1: (a + bi)(c + di) = ac + adi + bci + bdi 2 = ac + adi + bci + bd(– 1) = (ac – bd) + (ad + bc)i 28

Simplify an expression containing complex numbers Complex Conjugates The complex numbers (a + bi) and (a – bi) are called complex conjugates. For example, (3 + 4 i) and (3 – 4 i) are complex conjugates. (5 – 7 i) and (5 + 7 i) are complex conjugates. 29

Simplify an expression containing complex numbers The product of the complex number a + bi and its complex conjugate a – bi is the real number a 2 + b 2, as the following work shows: (a + bi)(a – bi) = a 2 – abi + abi – b 2 i 2 = a 2 – b 2(– 1) Use the distributive property to remove Parentheses. i 2 = – 1 = a 2 + b 2 30

5. Rationalize the denominator of a fraction that contains a complex number 31

Rationalize the denominator of a fraction that contains a complex number If b 0, the complex number a + bi contains the square root i=. Since a square root cannot remain in the denominator of a fraction, we often have to rationalize a denominator when dividing complex numbers. 32

Example 7 Divide and write the result in a + bi form: . Solution: We can rationalize the denominator by multiplying the numerator and the denominator by the complex conjugate of the denominator. Multiply the numerator and denominator by the complex conjugate of the denominator. Multiply. 33

Example 7 – Solution cont’d i 2 = – 1 Subtract. Write the result in a + bi form. 34

Rationalize the denominator of a fraction that contains a complex number Comment To avoid mistakes, always put complex numbers in a + bi form prior to performing any operations with complex numbers. 35

6. Find a specified power of i and apply this pattern to simplifying an expression 36

Find a specified power of i and apply this pattern to simplifying an expression The powers of i produce an interesting pattern: i= i 2 = =i = – 1 i 5 = i 4 i = 1 i = i i 6 = i 4 i 2 = 1(– 1) = – 1 i 3 = i 2 i = – 1 i = –i i 7 = i 4 i 3 = 1(–i) = –i i 4 = i 2 i 2 = (– 1) = 1 i 8 = i 4 i 4 = (1)(1) = 1 The pattern continues: i, – 1, –i, 1, . . When simplifying a specified power of i the calculation is easier if we can write the expression in terms of i 4 since i 4 = 1. 37

Find a specified power of i and apply this pattern to simplifying an expression If there is a remainder when the exponent is divided by 4, use the pattern i, – 1, –i, 1 to simplify the expression as illustrated in the next example. 38

Example 10 Simplify: i 29 Solution: We note that 29 divided by 4 gives a quotient of 7 and a remainder of 1. Thus, 29 = 4 7 + 1, and i 29 = i 4 7 + 1 29 = 4 7 + 1 = (i 4 )7 i i 4 7 + 1 = i 4 7 i 1 = (i 4)7 i = 17 i i 4=1 =i 39

Find a specified power of i and apply this pattern to simplifying an expression Powers of i If n is a natural number that has a remainder of r when divided by 4, then i n = i r. When n is divisible by 4, the remainder r is 0 and i 0 = 1. 40

7. Find the absolute value of a complex number 41

Find the absolute value of a complex number Absolute Value of a Complex Number The absolute value of the complex number a + bi is In symbols, | a + bi | = 42

Example 13 Find each absolute value. a. b. 43

Example 13 cont’d c. d. 44
 Rational and radical equations
Rational and radical equations Radical functions and rational exponents unit test
Radical functions and rational exponents unit test How is using exponents helpful
How is using exponents helpful Copyright cengage learning. powered by cognero
Copyright cengage learning. powered by cognero Differentiate like radicals from unlike radicals
Differentiate like radicals from unlike radicals What is an entire radical
What is an entire radical Simplify calculator
Simplify calculator Lesson 5 negative exponents
Lesson 5 negative exponents Exponents algebra 2
Exponents algebra 2 5-6 radical expressions and rational exponents
5-6 radical expressions and rational exponents Radicals and complex numbers
Radicals and complex numbers 5-6 radical expressions and rational exponents
5-6 radical expressions and rational exponents 6-6 rational exponents
6-6 rational exponents 11-3 solving radical equations
11-3 solving radical equations Unit 6 radical functions homework 6 radical equations
Unit 6 radical functions homework 6 radical equations Apply properties of rational exponents
Apply properties of rational exponents Simplify rational exponents
Simplify rational exponents 6-2 rational exponents
6-2 rational exponents Unit 6 radical functions homework 8
Unit 6 radical functions homework 8 Rational exponents
Rational exponents Square root rules
Square root rules Evaluating nth roots
Evaluating nth roots How to do fraction exponents
How to do fraction exponents Use the properties of exponents to rewrite each expression
Use the properties of exponents to rewrite each expression Delmar cengage learning medical terminology
Delmar cengage learning medical terminology Chapter 5 the cardiovascular system labeling exercises
Chapter 5 the cardiovascular system labeling exercises Cengage learning heart diagram
Cengage learning heart diagram South-western cengage learning
South-western cengage learning Chapter 13 medical math
Chapter 13 medical math 2009 delmar cengage learning
2009 delmar cengage learning Cengage learning heart diagram
Cengage learning heart diagram Introduction to medical terminology chapter 1 answer key
Introduction to medical terminology chapter 1 answer key Cengage learning australia
Cengage learning australia Graphing tpr
Graphing tpr Whille
Whille Cengage learning
Cengage learning Wadsworth cengage learning
Wadsworth cengage learning Cengage learning
Cengage learning Cengage learning plant cell
Cengage learning plant cell Cengage learning
Cengage learning Cengage learning
Cengage learning Brooks cole cengage learning
Brooks cole cengage learning Chapter 7:10 respitory system
Chapter 7:10 respitory system 2014 cengage learning accounting answers
2014 cengage learning accounting answers Cengage learning
Cengage learning