Quick Proofs T Madas T Madas Claim For

Claim: “For every positive whole number n, the value of 6 n – 1

Imagine a 10 by 10 grid of numbers. Place a square with 4 boxes

• • • Take 5 consecutive numbers Ignore the middle number Multiply the

• Take any two digit number • Reverse its digits • Prove the

Prove that the square of an odd number is also odd • • How

Prove that the difference between the squares of any two odd positive integers is

Prove that the product of any 4 consecutive positive integers plus 1, is always

Prove that the product of any 2 consecutive positive integers a and b and

Prove algebraically that the product of any two consecutive terms of the sequence 3,

Slides: 25

Download presentation

Quick Proofs © T Madas

Claim: “For every positive whole number n, the value of 6 n – 1 is always a prime number”. Prove by a counter-example that this statement is not true. n=1 n=2 n=3 n=4 n=5 n=6 6 n 6 n 6 n – – – 1= 1= 1= 5 11 17 23 29 35 prime prime not a prime The above statement is not true © T Madas

Imagine a 10 by 10 grid of numbers. Place a square with 4 boxes anywhere on the grid Multiply the numbers in the boxes which are diagonally opposite. Prove that the difference between the two answers will always be 10 1 2 3 4 5 6 7 8 9 10 32 x 23 = 736 11 12 13 14 15 16 17 18 19 20 33 x 22 = 726 21 22 23 24 25 26 27 28 29 30 10 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 n n+1 n + 10 n + 11 © T Madas

Imagine a 10 by 10 grid of numbers. Place a square with 4 boxes anywhere on the grid Multiply the numbers in the boxes which are diagonally opposite. Prove that the difference between the two answers will always be 10 (n + 10)(n + 1) = n 2 + n + 10 = n 2 + 11 n + 10 n (n + 11) = n 2 + 11 n 10 32 x 23 = 736 33 x 22 = 726 10 n n+1 n + 10 n + 11 Can you prove that in any size grid the difference will always be equal to the grid size? © T Madas

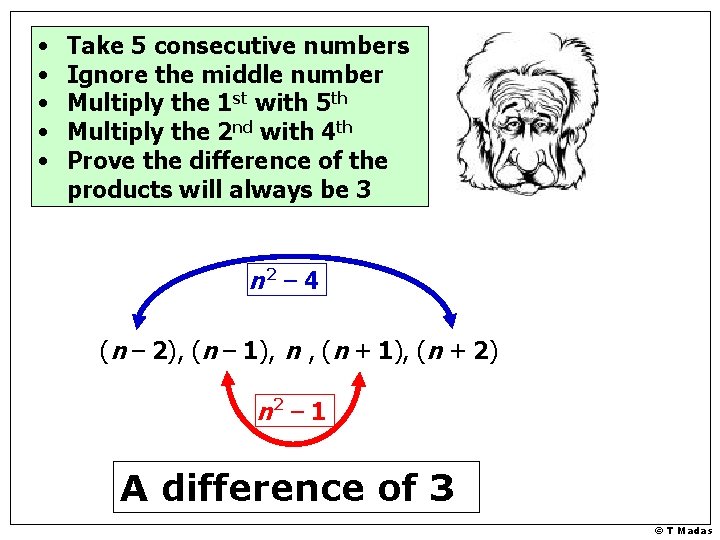
• • • Take 5 consecutive numbers Ignore the middle number Multiply the 1 st with 5 th Multiply the 2 nd with 4 th Prove the difference of the products will always be 3 n 2 – 4 (n – 2), (n – 1), n , (n + 1), (n + 2) n 2 – 1 A difference of 3 © T Madas

• Take any two digit number • Reverse its digits • Prove the sum of the original and the newly formed number will always be a multiple of 11 • Prove the difference between the original and the newly formed number will always be a multiple of 9 Let the original two digit number be 10 a + b where a are the tens and b are the units of the number Reversing the digits produces the number 10 b + a Adding the two numbers: (10 a + b ) + (10 b + a ) = 10 a + b + 10 b + a = 11 a + 11 b = 11(a + b) Subtracting the two numbers, assuming a > b: (10 a + b ) – (10 b + a ) = 10 a + b – 10 b – a = 9 a – 9 b = 9(a – b) Subtracting the two numbers, assuming b > a: (10 b + a ) – (10 a + b ) = 10 b + a – 10 a – b = 9 b – 9 a = 9(b – a) © T Madas

Prove that the square of an odd number is also odd • • How do we write an odd number using algebra ? If n is any positive integer is 2 n odd or even ? What about 2 n + 1 ? What about 2 n – 1 ? [ 2 n + 1 ] 2 = 4 n 2 + 4 n + 1 = 2[2 n 2 – 2 n ] + 1 = 2 p + 1 © T Madas

Prove that the difference between the squares of any two odd positive integers is a multiple of 8 E. g. 32 – 12 = 8= 8 x 1 52 – 12 = 24 = 8 x 3 52 – 32 = 16 = 8 x 2 72 – 12 = 48 = 8 x 6 72 – 32 = 40 = 8 x 5 72 – 52 = 24 = 8 x 3 92 – 12 = 80 = 8 x 10 92 – 32 = 72 = 8 x 9 92 – 52 = 56 = 8 x 7 92 – 72 = 32 = 8 x 4 © T Madas

Prove that the difference between the squares of any two odd positive integers is a multiple of 8 Let the two odd positive integers be 2 n + 1 and 2 m + 1 where m > n [2 m + 1]2 – [ 2 n + 1]2 = [2 m + 1 + 2 n + 1 ] [ 2 m + 1 – 2 n – 1] = [ 2 m + 2 n + 2 ] [ 2 m – 2 n] = 4 [ m + n + 1 ] [ m – n] If both m and n are even: If both m and n are odd: If m is even and n is odd: If m is odd and n is even: m – n is even m + n + 1 is even the expression 4[m + n + 1][m – n] is a multiple of 8 © T Madas

Prove that the product of any 4 consecutive positive integers plus 1, is always a perfect square root 1 x 2 x 3 x 4+ 1 = 25 = 5 2 x 3 x 4 x 5 + 1 = 121 = 11 3 x 4 x 5 x 6 + 1 = 361 = 19 ……… ……… 4 x 5 x 6 x 7 + 1 = 841 = 29 n (n + 1)(n + 2)(n + 3)+ 1 = (n 2 + n)(n 2 + 5 n + 6) + 1 = n 4 + 5 n 3 + 6 n 2 + n 3 + 5 n 2 + 6 n + 1 = n 4 + 6 n 3 + 11 n 2 + 6 n + 1 = (n 2 + 3 n + 1 )2 = n 2 + 3 n + 1 © T Madas

Prove that the product of any 2 consecutive positive integers a and b and their product c, satisfy the 3 D Pythagorean relationship a 2 + b 2 + c 2 = d 2 , with d a positive integer Let a = n b=n+1 c = n (n + 1) = n 2 + n n 2 + (n + 1)2 + (n 2 + n)2 = = = n 2 + 2 n + 1 + n 4 + 2 n 3 + n n 4 + 2 n 3 + 2 n 2 + 3 n + 1 (n 2 + n + 1 )2 © T Madas

Prove algebraically that the product of any two consecutive terms of the sequence 3, 8, 15, 24, 35, 48 … can be written as the product of 4 consecutive integers. Let us check this fact first: 3 x 8 = 1 x 2 x 3 x 4 8 x 15 = 2 x 3 x 4 x 5 15 x 24 = 3 x 4 x 5 x 6 n 1 2 3 4 5 6 un 3 8 15 24 35 48 … n … (n + 1) 2 – 1 n+1 (n + 2) 2 – 1 (n + 1) 2 – 1 (n + 2) 2 – 1 = n 2 + 2 n + 1 – 1 n 2 + 4 n + 4 – 1 = n 2 + 2 n n 2 + 4 n + 3 = There is another way of proving this result n (n + 2) (n + 1) (n + 3) © T Madas

Prove algebraically that the product of any two consecutive terms of the sequence 3, 8, 15, 24, 35, 48 … can be written as the product of 4 consecutive integers. Let us check this fact first: 3 x 8 = 1 x 2 x 3 x 4 8 x 15 = 2 x 3 x 4 x 5 15 x 24 = 3 x 4 x 5 x 6 n 1 2 3 4 5 6 un 3 8 15 24 35 48 … n … (n + 1) 2 – 1 un 1 x 3 2 x 4 3 x 5 4 x 6 5 x 7 6 x 8 … n (n + 2) n+1 (n + 2) 2 – 1 (n + 4) (n + 3) © T Madas