Properties of ContextFree Languages Decision Properties Closure Properties























![Formal Construction of P’ u States are pairs [q, b], where: 1. q is Formal Construction of P’ u States are pairs [q, b], where: 1. q is](https://slidetodoc.com/presentation_image_h/0eca6166b000ca2d86a52ac93e076a87/image-26.jpg)

![Transitions of P’ 1. δ’([q, ε], a, X) = {([q, h(a)], X)} for any Transitions of P’ 1. δ’([q, ε], a, X) = {([q, h(a)], X)} for any](https://slidetodoc.com/presentation_image_h/0eca6166b000ca2d86a52ac93e076a87/image-28.jpg)





![Formal Construction – (2) u. Accepting states of combined PDA are those [q, p] Formal Construction – (2) u. Accepting states of combined PDA are those [q, p]](https://slidetodoc.com/presentation_image_h/0eca6166b000ca2d86a52ac93e076a87/image-35.jpg)
- Slides: 35

Properties of Context-Free Languages Decision Properties Closure Properties 1

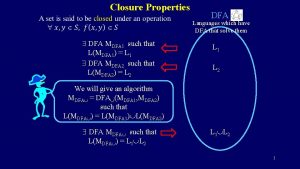
Summary of Decision Properties u As usual, when we talk about “a CFL” we really mean “a representation for the CFL, e. g. , a CFG or a PDA accepting by final state or empty stack. u There algorithms to decide if: 1. String w is in CFL L. 2. CFL L is empty. 3. CFL L is infinite. 2

Non-Decision Properties u. Many questions that can be decided for regular sets cannot be decided for CFL’s. u. Example: Are two CFL’s the same? u. Example: Are two CFL’s disjoint? w How would you do that for regular languages? u. Need theory of Turing machines and decidability to prove no algorithm exists. 3

Testing Emptiness u. We already did this. u. We learned to eliminate variables that generate no terminal string. u. If the start symbol is one of these, then the CFL is empty; otherwise not. 4

Testing Membership u. Want to know if string w is in L(G). u. Assume G is in CNF. w Or convert the given grammar to CNF. w w = ε is a special case, solved by testing if the start symbol is nullable. u. Algorithm (CYK ) is a good example of dynamic programming and runs in time O(n 3), where n = |w|. 5

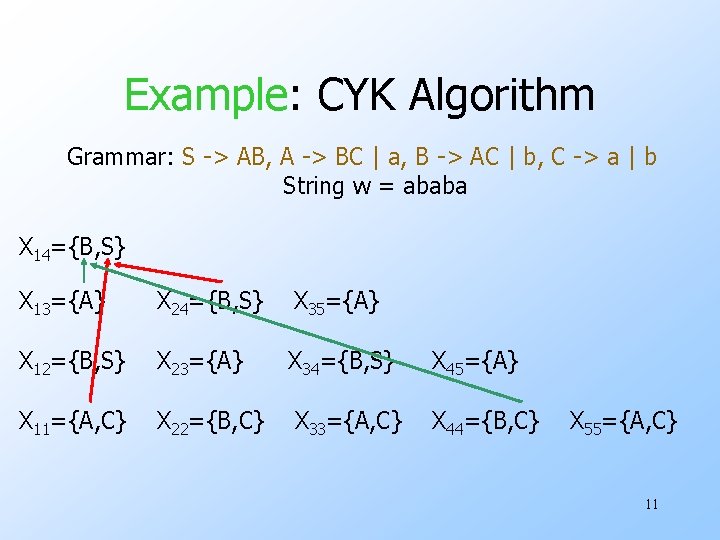
CYK Algorithm u. Let w = a 1…an. u. We construct an n-by-n triangular array of sets of variables. u. Xij = {variables A | A =>* ai…aj}. u. Induction on j–i+1. w The length of the derived string. u. Finally, ask if S is in X 1 n. 6

CYK Algorithm – (2) u. Basis: Xii = {A | A -> ai is a production}. u. Induction: Xij = {A | there is a production A -> BC and an integer k, with i < k < j, such that B is in Xik and C is in Xk+1, j. 7

Example: CYK Algorithm Grammar: S -> AB, A -> BC | a, B -> AC | b, C -> a | b String w = ababa X 12={B, S} X 23={A} X 34={B, S} X 45={A} X 11={A, C} X 22={B, C} X 33={A, C} X 44={B, C} X 55={A, C} 8

Example: CYK Algorithm Grammar: S -> AB, A -> BC | a, B -> AC | b, C -> a | b String w = ababa X 13={} Yields nothing X 12={B, S} X 23={A} X 34={B, S} X 45={A} X 11={A, C} X 22={B, C} X 33={A, C} X 44={B, C} X 55={A, C} 9

Example: CYK Algorithm Grammar: S -> AB, A -> BC | a, B -> AC | b, C -> a | b String w = ababa X 13={A} X 24={B, S} X 35={A} X 12={B, S} X 23={A} X 34={B, S} X 45={A} X 11={A, C} X 22={B, C} X 33={A, C} X 44={B, C} X 55={A, C} 10

Example: CYK Algorithm Grammar: S -> AB, A -> BC | a, B -> AC | b, C -> a | b String w = ababa X 14={B, S} X 13={A} X 24={B, S} X 35={A} X 12={B, S} X 23={A} X 34={B, S} X 45={A} X 11={A, C} X 22={B, C} X 33={A, C} X 44={B, C} X 55={A, C} 11

Example: CYK Algorithm Grammar: S -> AB, A -> BC | a, B -> AC | b, C -> a | b String w = ababa X 15={A} X 14={B, S} X 25={A} X 13={A} X 24={B, S} X 35={A} X 12={B, S} X 23={A} X 34={B, S} X 45={A} X 11={A, C} X 22={B, C} X 33={A, C} X 44={B, C} X 55={A, C} 12

Testing Infiniteness u. The idea is essentially the same as for regular languages. u. Use the pumping lemma constant n. u. If there is a string in the language of length between n and 2 n-1, then the language is infinite; otherwise not. u. Let’s work this out in class. 13

Closure Properties of CFL’s u. CFL’s are closed under union, concatenation, and Kleene closure. u. Also, under reversal, homomorphisms and inverse homomorphisms. u. But not under intersection or difference. 14

Closure of CFL’s Under Union u. Let L and M be CFL’s with grammars G and H, respectively. u. Assume G and H have no variables in common. w Names of variables do not affect the language. u. Let S 1 and S 2 be the start symbols of G and H. 15

Closure Under Union – (2) u. Form a new grammar for L M by combining all the symbols and productions of G and H. u. Then, add a new start symbol S. u. Add productions S -> S 1 | S 2. 16

Closure Under Union – (3) u. In the new grammar, all derivations start with S. u. The first step replaces S by either S 1 or S 2. u. In the first case, the result must be a string in L(G) = L, and in the second case a string in L(H) = M. 17

Closure of CFL’s Under Concatenation u. Let L and M be CFL’s with grammars G and H, respectively. u. Assume G and H have no variables in common. u. Let S 1 and S 2 be the start symbols of G and H. 18

Closure Under Concatenation – (2) u. Form a new grammar for LM by starting with all symbols and productions of G and H. u. Add a new start symbol S. u. Add production S -> S 1 S 2. u. Every derivation from S results in a string in L followed by one in M. 19

Closure Under Star u. Let L have grammar G, with start symbol S 1. u. Form a new grammar for L* by introducing to G a new start symbol S and the productions S -> S 1 S | ε. u. A rightmost derivation from S generates a sequence of zero or more S 1’s, each of which generates some string in L. 20

Closure of CFL’s Under Reversal u. If L is a CFL with grammar G, form a grammar for LR by reversing the right side of every production. u. Example: Let G have S -> 0 S 1 | 01. u. The reversal of L(G) has grammar S -> 1 S 0 | 10. 21

Closure of CFL’s Under Homomorphism u. Let L be a CFL with grammar G. u. Let h be a homomorphism on the terminal symbols of G. u. Construct a grammar for h(L) by replacing each terminal symbol a by h(a). 22

Example: Closure Under Homomorphism u. G has productions S -> 0 S 1 | 01. uh is defined by h(0) = ab, h(1) = ε. uh(L(G)) has the grammar with productions S -> ab. S | ab. 23

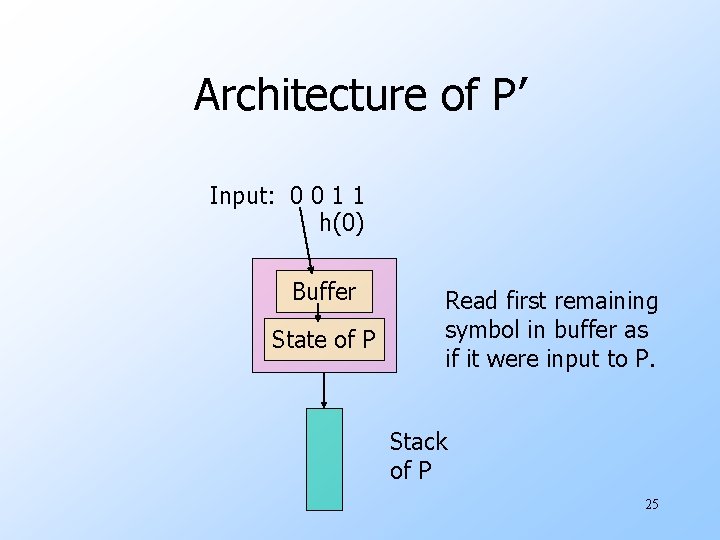
Closure of CFL’s Under Inverse Homomorphism u. Here, grammars don’t help us. u. But a PDA construction serves nicely. u. Intuition: Let L = L(P) for some PDA P. u. Construct PDA P’ to accept h-1(L). u. P’ simulates P, but keeps, as one component of a two-component state a buffer that holds the result of applying h to one input symbol. 24

Architecture of P’ Input: 0 0 1 1 h(0) Buffer State of P Read first remaining symbol in buffer as if it were input to P. Stack of P 25
![Formal Construction of P u States are pairs q b where 1 q is Formal Construction of P’ u States are pairs [q, b], where: 1. q is](https://slidetodoc.com/presentation_image_h/0eca6166b000ca2d86a52ac93e076a87/image-26.jpg)
Formal Construction of P’ u States are pairs [q, b], where: 1. q is a state of P. 2. b is a suffix of h(a) for some symbol a. u Thus, only a finite number of possible values for b. u Stack symbols of P’ are those of P. u Start state of P’ is [q 0 , ε]. 26

Construction of P’ – (2) u. Input symbols of P’ are the symbols to which h applies. u. Final states of P’ are the states [q, ε] such that q is a final state of P. 27
![Transitions of P 1 δq ε a X q ha X for any Transitions of P’ 1. δ’([q, ε], a, X) = {([q, h(a)], X)} for any](https://slidetodoc.com/presentation_image_h/0eca6166b000ca2d86a52ac93e076a87/image-28.jpg)
Transitions of P’ 1. δ’([q, ε], a, X) = {([q, h(a)], X)} for any input symbol a of P’ and any stack symbol X. 1. When the buffer is empty, P’ can reload it. 2. δ’([q, bw], ε, X) contains ([p, w], ) if δ(q, b, X) contains (p, ), where b is either an input symbol of P or ε. 1. Simulate P from the buffer. 28

Proving Correctness of P’ u. We need to show that L(P’) = h-1(L(P)). u. Key argument: P’ makes the transition ([q 0, ε], w, Z 0)⊦*([q, x], ε, ) if and only if P makes transition (q 0, y, Z 0) ⊦*(q, ε, ), h(w) = yx, and x is a suffix of the last symbol of w. u. Proof in both directions is an induction on the number of moves made. 29

Nonclosure Under Intersection u. Unlike the regular languages, the class of CFL’s is not closed under . u. We know that L 1 = {0 n 1 n 2 n | n > 1} is not a CFL (use the pumping lemma). u. However, L 2 = {0 n 1 n 2 i | n > 1, i > 1} is. w CFG: S -> AB, A -> 0 A 1 | 01, B -> 2 B | 2. u. So is L 3 = {0 i 1 n 2 n | n > 1, i > 1}. u. But L 1 = L 2 L 3. 30

Nonclosure Under Difference u. We can prove something more general: w Any class of languages that is closed under difference is closed under intersection. u. Proof: L M = L – (L – M). u. Thus, if CFL’s were closed under difference, they would be closed under intersection, but they are not. 31

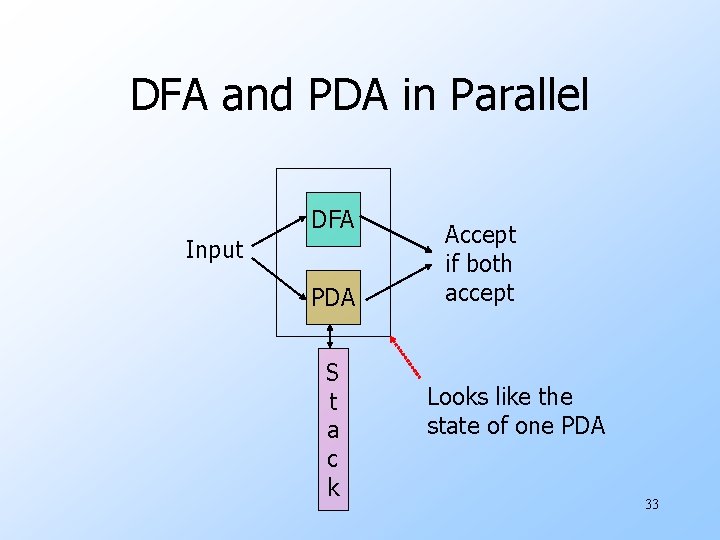
Intersection with a Regular Language u. Intersection of two CFL’s need not be context free. u. But the intersection of a CFL with a regular language is always a CFL. u. Proof involves running a DFA in parallel with a PDA, and noting that the combination is a PDA. w PDA’s accept by final state. 32

DFA and PDA in Parallel DFA Input PDA S t a c k Accept if both accept Looks like the state of one PDA 33

Formal Construction u. Let the DFA A have transition function δA. u. Let the PDA P have transition function δP. u. States of combined PDA are [q, p], where q is a state of A and p a state of P. uδ([q, p], a, X) contains ([δA(q, a), r], ) if δP(p, a, X) contains (r, ). w Note a could be , in which case δA(q, a) = q. 34
![Formal Construction 2 u Accepting states of combined PDA are those q p Formal Construction – (2) u. Accepting states of combined PDA are those [q, p]](https://slidetodoc.com/presentation_image_h/0eca6166b000ca2d86a52ac93e076a87/image-35.jpg)
Formal Construction – (2) u. Accepting states of combined PDA are those [q, p] such that q is an accepting state of A and p is an accepting state of P. u. Easy induction: ([q 0, p 0], w, Z 0)⊦* ([q, p], , ) if and only if δA(q 0, w) = q and in P: (p 0, w, Z 0)⊦*(p, , ). 35
 Decision properties of cfl
Decision properties of cfl Cfl is not closed under complementation
Cfl is not closed under complementation Inverse homomorphism in regular languages
Inverse homomorphism in regular languages Right linear grammar to left linear grammar
Right linear grammar to left linear grammar No decision snap decision responsible decision
No decision snap decision responsible decision Slidetodoc.com
Slidetodoc.com Decision properties of regular languages
Decision properties of regular languages Decision properties of regular languages
Decision properties of regular languages Decision properties of regular languages
Decision properties of regular languages Decision properties of regular languages
Decision properties of regular languages Decision properties of context free languages
Decision properties of context free languages Decision properties of context free languages
Decision properties of context free languages Closure properties of context free grammar
Closure properties of context free grammar Np closure properties
Np closure properties Closure properties of dfa
Closure properties of dfa What operations are polynomials closed under
What operations are polynomials closed under Decision table and decision tree examples
Decision table and decision tree examples Properties of regular languages
Properties of regular languages Contoh super key
Contoh super key Laa closure watchman
Laa closure watchman Skill of questioning in microteaching with examples
Skill of questioning in microteaching with examples Closure-oriented/judging vs. open/perceiving
Closure-oriented/judging vs. open/perceiving Watchman truseal
Watchman truseal Vena seal
Vena seal Shortest paths and transitive closure in data structure
Shortest paths and transitive closure in data structure Closure property
Closure property Floyd warshall algorithm transitive closure
Floyd warshall algorithm transitive closure Nnnn aesthetic
Nnnn aesthetic Perpetual project closure
Perpetual project closure Closure ketergantungan fungsional
Closure ketergantungan fungsional Lane closure system
Lane closure system Strong triadic closure property
Strong triadic closure property Perpetual project closure
Perpetual project closure Section 1 topic 8 operations with polynomials
Section 1 topic 8 operations with polynomials Robot coin collection dynamic programming
Robot coin collection dynamic programming Closure meaning
Closure meaning