Prof Harvinder Kaur PG Govt College for Girls

Prof. Harvinder Kaur PG Govt College for Girls Sector-11, Chandigarh

Outline v Reciprocal Lattice of various crystals v Simple cubic lattice v Face-centered cubic lattice v Body-centered cubic lattice v Bragg law of Diffraction v Experimental Diffraction methods v Structure and Form factor

Reciprocal Lattice The reciprocal lattice of a Bravais Lattice is the set of all vectors K such that ei. K. R = 1 for all lattice point position vectors R. This reciprocal lattice is itself a Bravais lattice, and the reciprocal of the reciprocal lattice is the original lattice. For an infinite three dimensional lattice, defined by its primitive vectors, its reciprocal lattice can be determined by generating its three reciprocal primitive vectors, through the formulae

Properties Of Reciprocal Lattice Ø Direct lattice is a lattice in ordinary space whereas the reciprocal lattice is a lattice in the Fourier space. Ø The primitive vectors in reciprocal lattice has the dimensions of (length)-1 whereas the primitive vectors of the direct lattice have the dimensions of length Ø A diffraction pattern of a crystal is a map of the reciprocal lattice of the crystal whereas a microscopic image is a map of direct lattice Ø When we rotate a crystal, both direct and reciprocal lattice rotates Ø Each point in the reciprocal lattice represents a set of parallel planes of the crystal lattice Ø If the coordinates of reciprocal vector G have no common factor, then G is inversely proportional to the spacing of the lattice planes normal to G Ø The volume of unit cell of the reciprocal lattice is inversely proportional to the volume of unit cell of the direct lattice Ø The direct lattice is the reciprocal of its own reciprocal lattice Ø The unit cell of the reciprocal lattice need not be parallelopiped

Reciprocal Lattice In Two Dimensions

Reciprocal Lattice of Simple Cubic Lattice The simple cubic Bravais, with cubic primitive cell of side a, has for its reciprocal a simple cubic lattice with a cubic primitive cell of side ( in the crystallographer's definition). The cubic lattice is therefore said to be self-dual, having the same symmetry in reciprocal space as in real space

Reciprocal lattice to Facecentered cubic The reciprocal lattice to an FCC lattice is the bodycentered cubic (BCC) lattice. FCC in real space BCC in fourier space

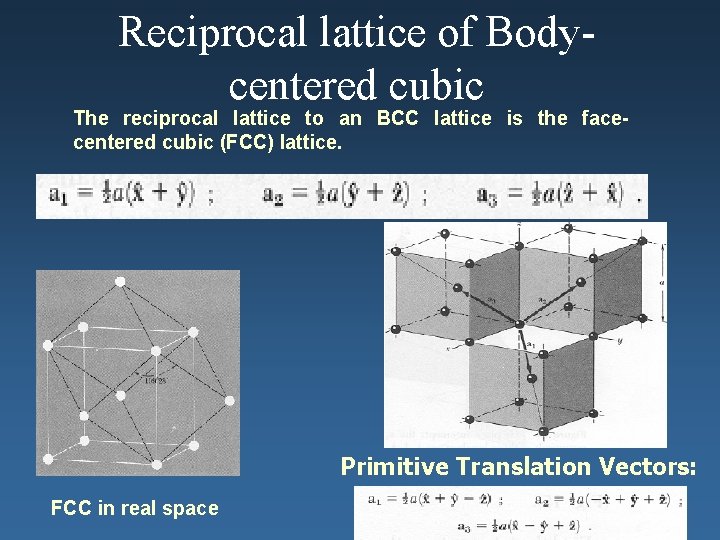
Reciprocal lattice of Bodycentered cubic The reciprocal lattice to an BCC lattice is the facecentered cubic (FCC) lattice. Primitive Translation Vectors: FCC in real space

Brillouin zones for FCC, BCC, HCP Real: FCC Reciprocal: BCC Reciprocal: FCC HCP

Bragg law of Diffraction Prof. W. L. Bragg observed that X-rays can be reflected by the cleavage planes of the crystal as if these parallel planes were acting like mirrors to the light beam. The reflected beam lead to well defined diffraction patterns on a photographic plane. The cleavage planes are atomic planes of a crystal that are systematically stacked one over the other as a parallel set of planes. X-rays from the incident plane can penetrate deeper into a target crystal and get reflected. Thus, several beams of Xray reflected from various planes are obtained. The final diffracted beam is the result of the superposition of these beams. Bragg law, 2 dsin = n where, d is the interplanar spacing, is the wavelength of incident X rays and is the angle of reflection

Bragg law of Diffraction Significance of Bragg’s law Ø Bragg’s law is a consequence of periodicity of the lattice Ø The law does not refer to the arrangement of atoms in the basis associated with each lattice point Ø The composition of the basis determine the relative intensity of the various orders n of diffraction Ø Since ~ 1 Ao is inevitable, we can’t use visible light for such studies

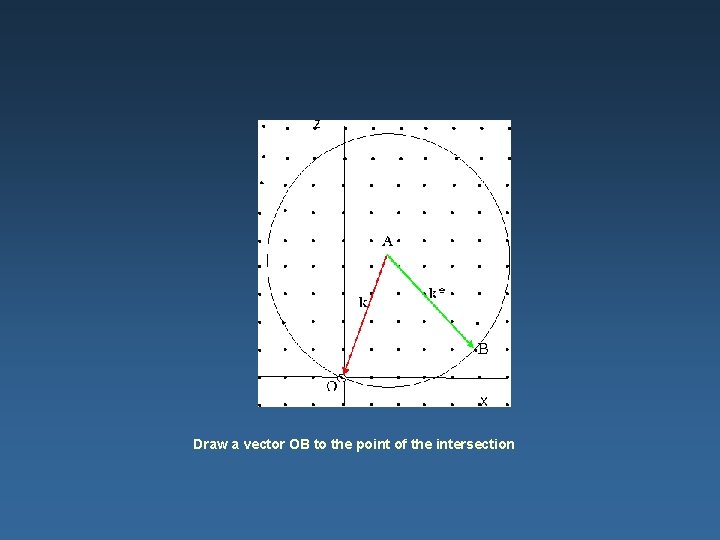
Bragg law in Reciprocal Lattice (Ewald Construction) Chose a point according to the orientation of the specimen with respect to the incident beam. Draw a vector AO in the incident direction of length 2 p/l terminating at the origin

(Ewald Construction) Construct a circle of radius 2 p/l with center at A. Note whether this circle passes through any point of the reciprocal lattice; if it does. . Draw a vector AB to the point of the intersection

Draw a vector OB to the point of the intersection

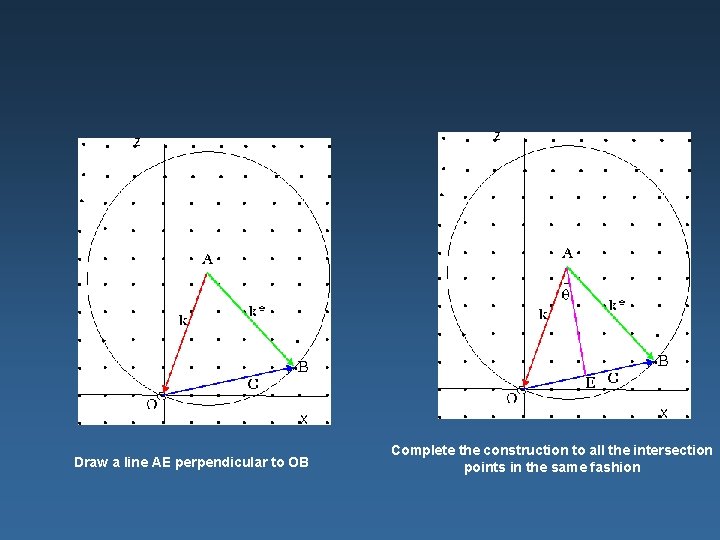
Draw a line AE perpendicular to OB Complete the construction to all the intersection points in the same fashion

By means of the Ewald construction we can write the Bragg law in vector form: Let G = OB and k = AO. For diffraction, it is necessary that the vector k + G, that is, the vector AB, be equal in magnitude to the vector k or (k + G)2 = k 2 or 2 k. G + G 2 = 0 (1) If we call the scattered wave vector k*, than k* = k + G (2) so we can write k*2 = k 2 (3) and k* - k = G, showing (2) that the scattering changes only the direction on k, and (3) that the scattered wave differs from the incident wave by a reciprocal lattice vector G. Equations (2) and (3) are the momentum and energy conservation law for x-ray diffraction, which is an example of elastic scattering. Whether or not the k circle intersects a lattice vector, and hence reflects, depends on its magnitude and orientation. Using (1) we can construct in the reciprocal lattice the locus of all those waves that can produce Bragg reflection. This locus represents a set of planes in three dimensions. The volume terminated by those planes is called Brillouin zone.

Experimental Diffraction Methods X-Ray Diffraction Method Laue Rotating Crystal Powder Orientation Single Crystal Polychromatic Beam Fixed Angle Lattice constant Single Crystal Monochromatic Beam Variable Angle Lattice Parameters Polycrystal (powdered) Monochromatic Beam Variable Angle

Experimental Diffraction Methods Laue’s Method : In this method a single crystal is held stationary in the path of a beam of em radiation (X-rays) or the Neutron radiation of continuous wavelengths. While is kept constant, the wavelength , is varied so that the Bragg law is satisfied. A plane film receives the diffracted beams. A developed film after its exposure shows a diffraction pattern that consists of series of spots. Laue spots in a diffraction pattern are actually map of the reciprocal lattice of the crystal under experiment.

Experimental Diffraction Methods Rotating Crystal Method : In this method , a single crystal is rotated about the fixed axis in a beam of monochromatic X-rays or neutrons. The angle is variable while the wavelength is kept constant. The variation of angle due to rotation of the crystal brings different atomic planes in the crystal into position for which Bragg’s reflection holds good. To record such reflections a film is mounted on a cylindrical holder that is concentric with a rotating spindle.

Experimental Diffraction Methods Powder Method : If a powdered specimen is used, instead of a single crystal, then there is no need to rotate the specimen, because there will always be some crystals at an orientation for which diffraction is permitted. Here a monochromatic X-ray beam is incident on a powdered or polycrystalline sample. This method is useful for samples that are difficult to obtain in single crystal form. The powder method is used to determine the value of the lattice parameters accurately. Lattice parameters are the magnitudes of the unit vectors a, b and c which define the unit cell for the crystal. For every set of crystal planes, by chance, one or more crystals will be in the correct orientation to give the correct Bragg angle to satisfy Bragg's equation. Every crystal plane is thus capable of diffraction. Each diffraction line is made up of a large number of small spots, each from a separate crystal. Each spot is so small as to give the appearance of a continuous line.

The Powder Method If a monochromatic x-ray beam is directed at a single crystal, then only one or two diffracted beams may result.

The Powder Method If the sample consists of some tens of randomly orientated single crystals, the diffracted beams are seen to lie on the surface of several cones. The cones may emerge in all directions, forwards and backwards.

The Powder Method A sample of some hundreds of crystals (i. e. a powdered sample) show that the diffracted beams form continuous cones. A circle of film is used to record the diffraction pattern as shown. Each cone intersects the film giving diffraction lines. The lines are seen as arcs on the film.

Structure and Form Factor A crystal is a periodic arrangement of atoms in a particular pattern. Each of the atoms may scatter incident radiation such as X-rays, electrons and neutrons. Because of the periodic arrangement of the atoms, the interference of waves scattered from different atoms may cause a distinct pattern of constructive and destructive interference to form. This is the diffraction pattern caused by the crystal. In the kinematical approximation for diffraction, the intensity of a diffracted beam is given by: where is the wave function of a beam scattered a vector , and is the so called structure factor which is given by: Here, rj is the position of an atom j in the unit cell, and fj is the scattering power of the atom, also called the atomic form factor. The sum is over all atoms in the unit cell. It can be shown that in the ideal case, diffraction only occurs if the scattering vector is equal to a reciprocal lattice vector .

Structure Factor For Specific Lattice Types Body-centered cubic (BCC) : As a convention, the body-centered cubic system is described in terms of a simple cubic lattice with primitive vectors ax, ay, az with the basis consisting of ro = 0 and r 1 = (a/2) (x+y+z). In a monoatomic crystal, all the form factors f are the same. The intensity of a diffracted beam scattered with a vector (2 /a) (hx+ky+lz) by a crystal plane with Miller indices given by (h, k, l)

Structure Factor Face Centered Cubic The face-centered cubic system is described as r 0 =0, r 1 = a/2(x+y), r 2 = (a/2)(y+z) r 3 = (a/2)(x+z) with indices given by (1/2, 0), (0, 1/2) and (1/2, 0, 1/2)