Potential energy surfaces for inelastic collisions Alexandre Faure

Potential energy surfaces for inelastic collisions Alexandre Faure, Claire Rist, Yohann Scribano, Pierre Valiron, Laurent Wiesenfeld Laboratoire d’Astrophysique de Grenoble Mathematical Methods for Ab Initio Quantum Chemistry, Nice, 14 th november 2008

Outline 1. Astrophysical context 2. Determining, monitoring and fitting multidimensional PESs 3. Computing scattering cross sections 4. Conclusions

1. Molecules in space

New windows on the « Molecular Universe » Herschel (2009) 490 5000 GHz ALMA (2010) 30 950 GHz

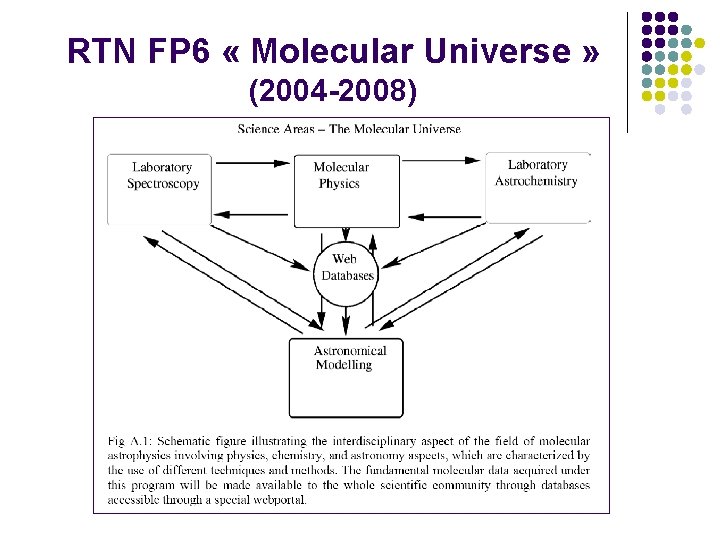
RTN FP 6 « Molecular Universe » (2004 -2008)

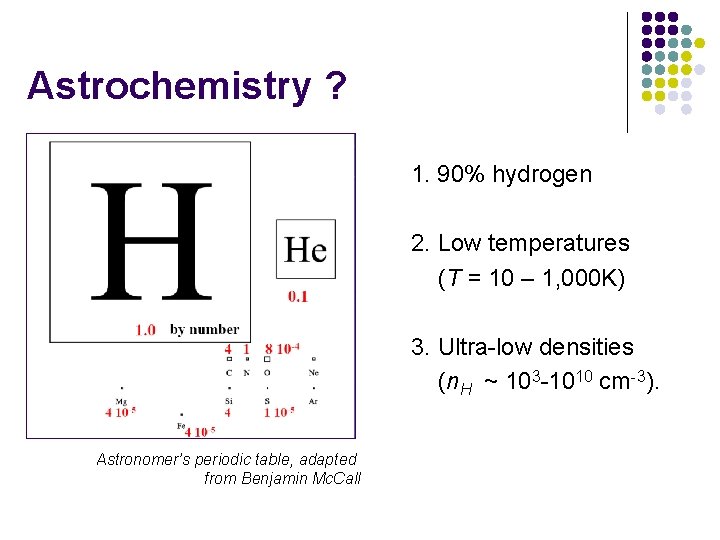
Astrochemistry ? 1. 90% hydrogen 2. Low temperatures (T = 10 – 1, 000 K) 3. Ultra-low densities (n. H ~ 103 -1010 cm-3). Astronomer’s periodic table, adapted from Benjamin Mc. Call

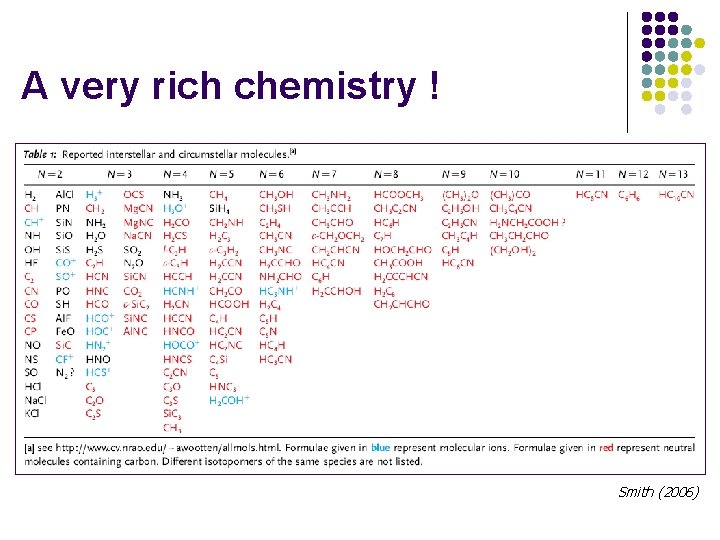
A very rich chemistry ! Smith (2006)

Molecules as probes of star formation Lada et al. (2003)

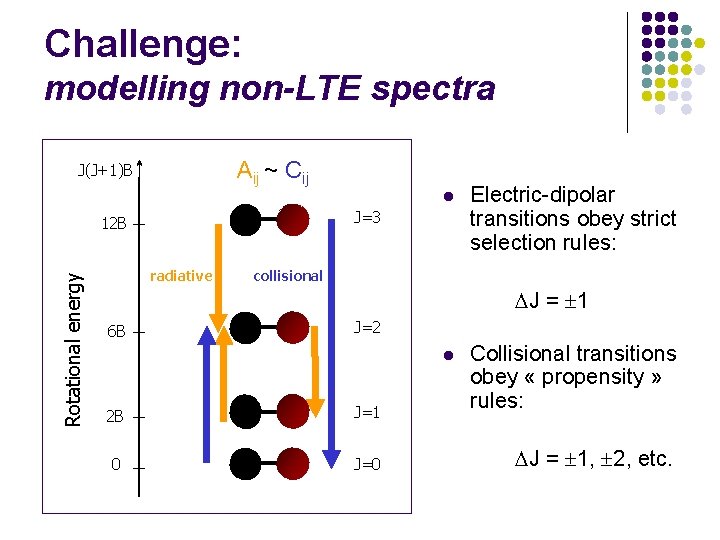
Challenge: modelling non-LTE spectra Aij ~ Cij J(J+1)B Rotational energy Electric-dipolar transitions obey strict selection rules: J = 1 l Collisional transitions obey « propensity » rules: J = 1, 2, etc. J=3 12 B radiative 6 B l collisional J=2 2 B J=1 0 J=0

Wanted: Collisional rate coefficients l M(j, v) + H 2(j 2, v 2) M(j’, v’) + H 2(j 2’, v 2’) l Collision energies from ~ 1 to 1, 000 cm-1, i. e. rotational excitation dominant l As measurements are difficult, numerical models rely on theoretical calculations.

2. Computing PESs

Born-Oppenheimer approximation l Electronic problem l Nuclear problem l Orbital approximation l « Electronic » PES l Hartree-Fock (variational principle) l Quantum dynamics: closecoupling, wavepackets l Electronic correlation (configuration interaction) l Semi or quasi-classical dynamics: trajectories

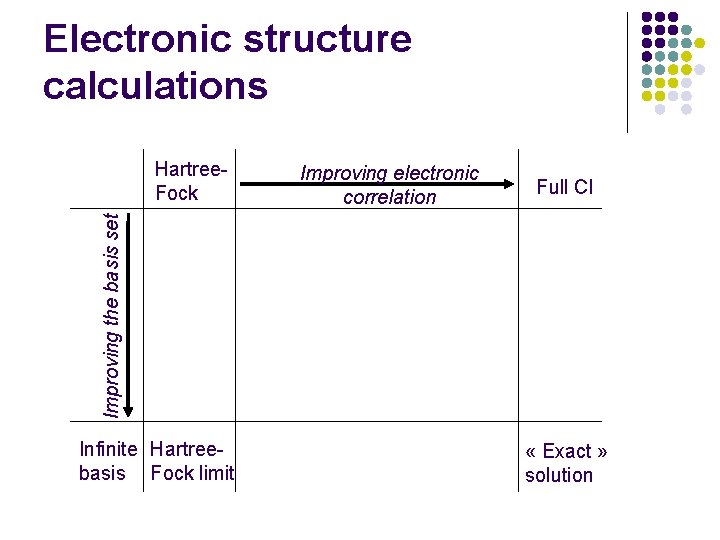
Electronic structure calculations Improving electronic correlation Full CI Improving the basis set Hartree. Fock Infinite Hartreebasis Fock limit « Exact » solution

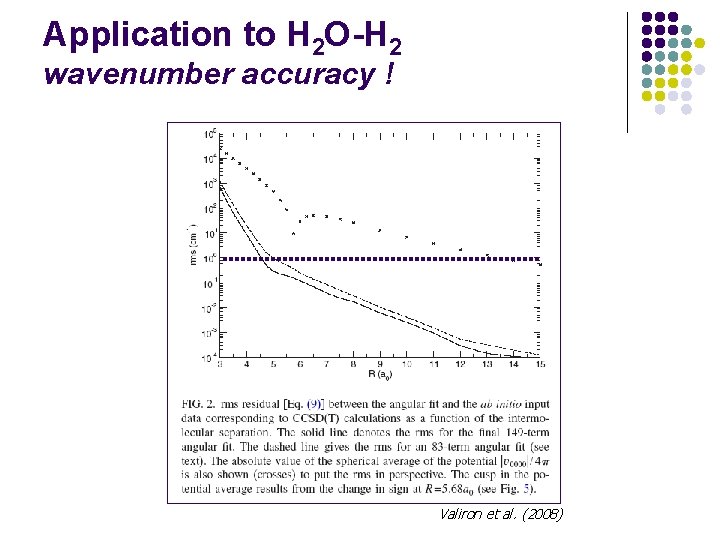
van der Waals interactions l The interaction energy is a negligible fraction of molecular energies: E(A-B) = E(AB) – E(A) –E(B) l For van der Waals complexes, the bonding energy is ~ 100 cm-1 l Wavenumber accuracy (~ 1 cm-1) required !

State-of-the-art: R 12 theory

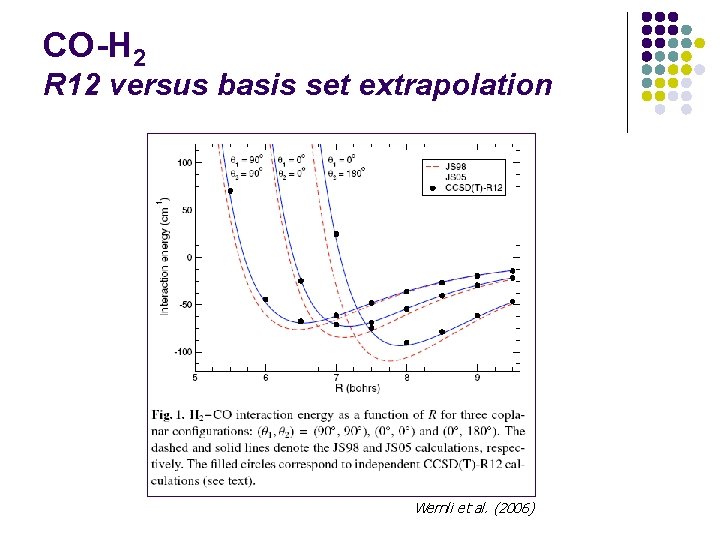
CO-H 2 R 12 versus basis set extrapolation Wernli et al. (2006)

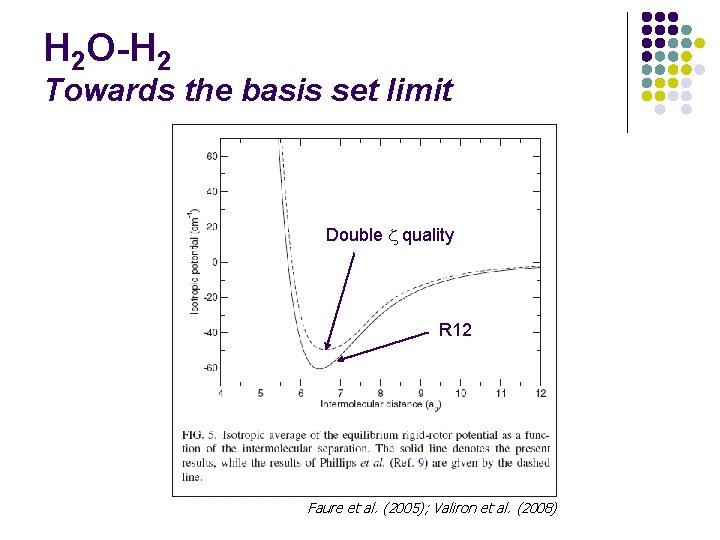
H 2 O-H 2 Towards the basis set limit Double quality R 12 Faure et al. (2005); Valiron et al. (2008)

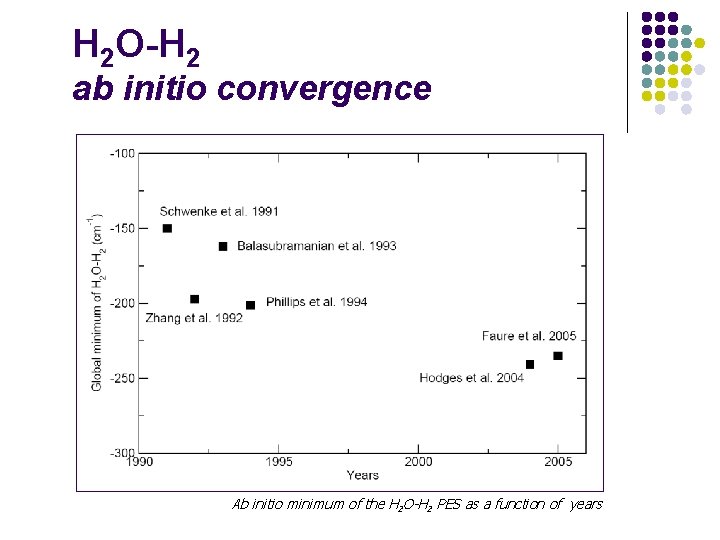
H 2 O-H 2 ab initio convergence Ab initio minimum of the H 2 O-H 2 PES as a function of years

Computational strategy l l where Faure et al. (2005); Valiron et al. (2008)

Expanding 5 D PES

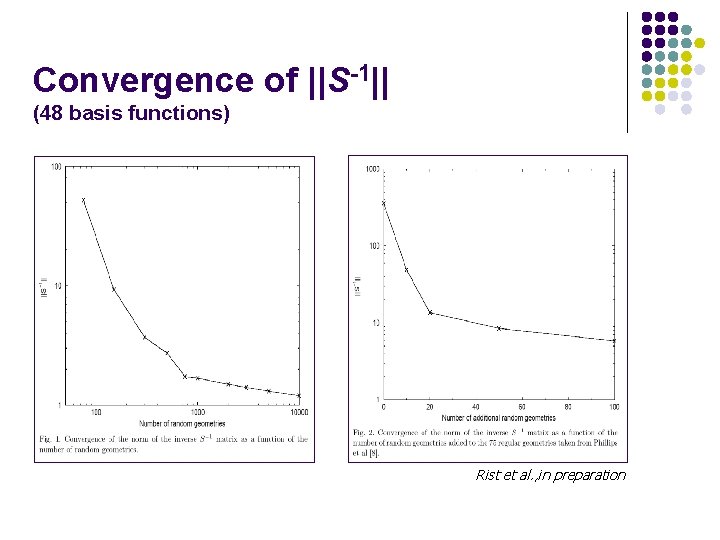
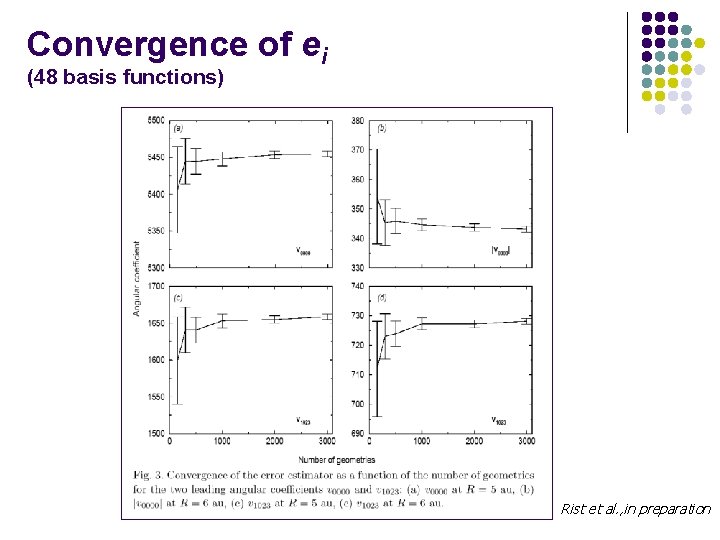
In preparation l Scalar products : l Sampling « estimator » : l Mean error:

Convergence of ||S-1|| (48 basis functions) Rist et al. , in preparation

Convergence of ei (48 basis functions) Rist et al. , in preparation

Application to H 2 O-H 2 wavenumber accuracy ! Valiron et al. (2008)

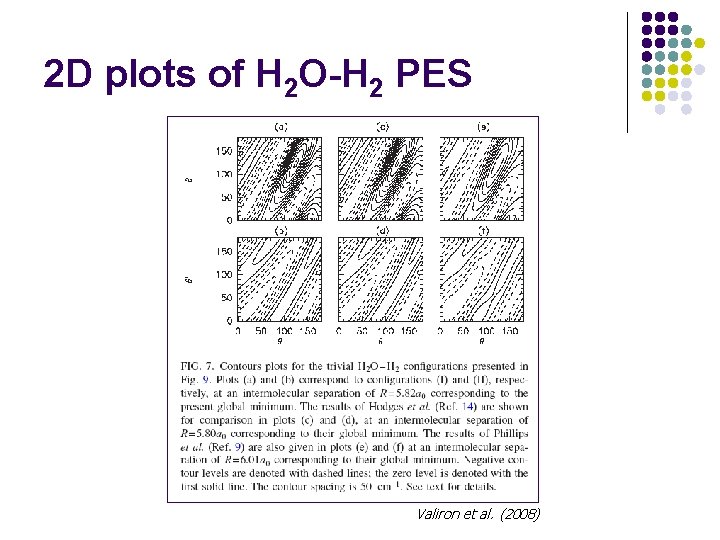
2 D plots of H 2 O-H 2 PES Valiron et al. (2008)

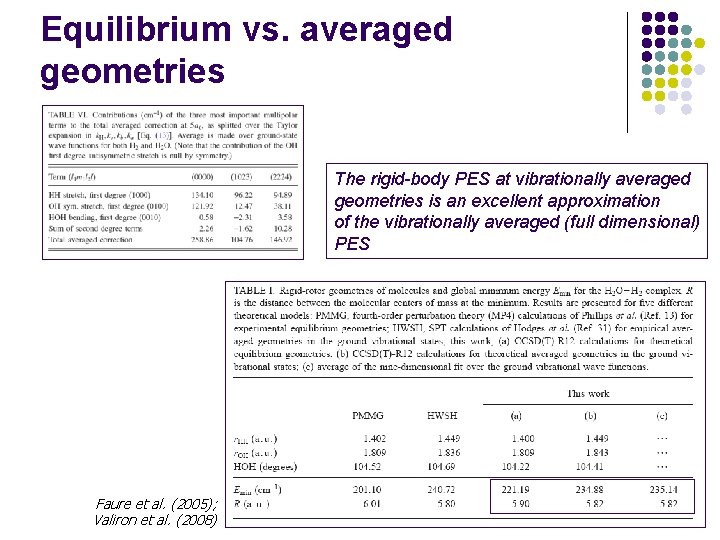
Equilibrium vs. averaged geometries The rigid-body PES at vibrationally averaged geometries is an excellent approximation of the vibrationally averaged (full dimensional) PES Faure et al. (2005); Valiron et al. (2008)

Current strategy l Monomer geometries: ground-state averaged l Reference surface at the CCSD(T)/aug-cc-p. VDZ (typically 50, 000 points) l Complete basis set extrapolation (CBS) based on CCSD(T)/aug -cc-p. VTZ (typically 5, 000 points) l Monte-Carlo sampling, « monitored » angular fitting (typically 100 -200 basis functions) l Cubic spline radial extrapolation (for short and long-range)

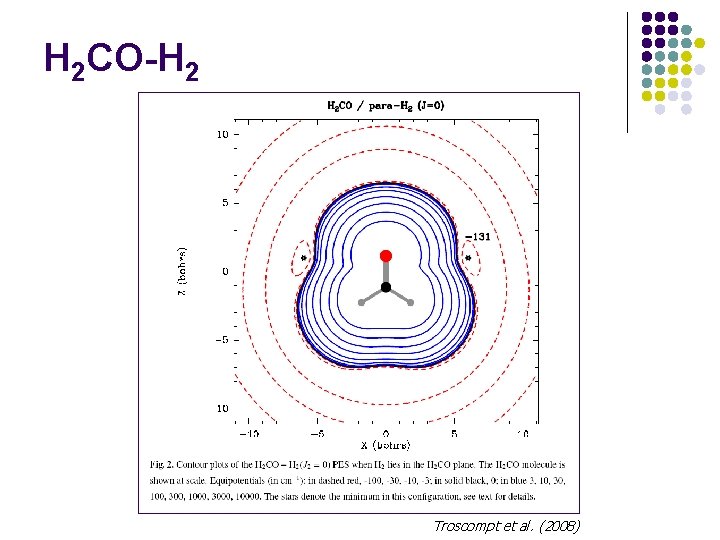
H 2 CO-H 2 Troscompt et al. (2008)

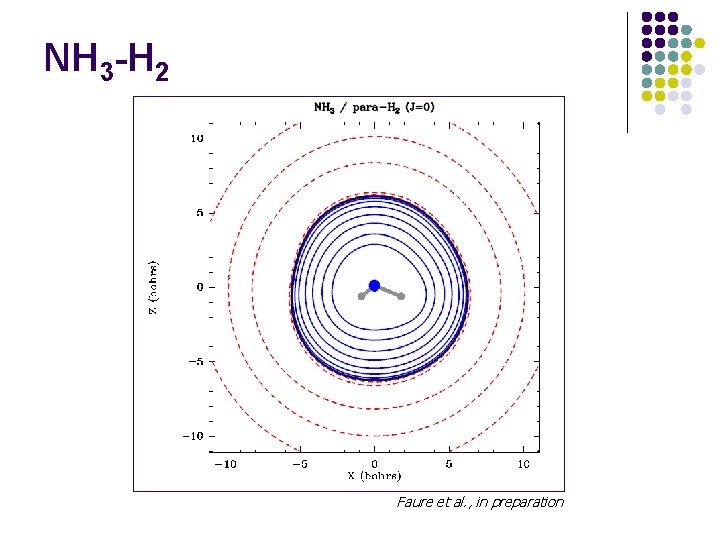
NH 3 -H 2 Faure et al. , in preparation

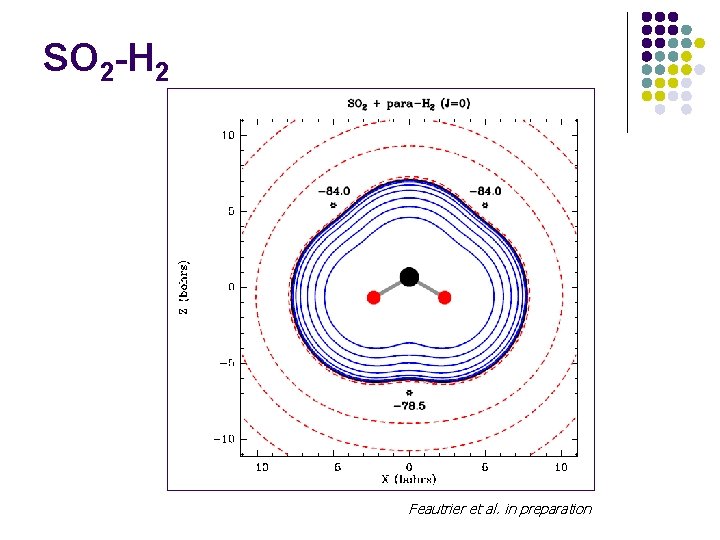
SO 2 -H 2 Feautrier et al. in preparation

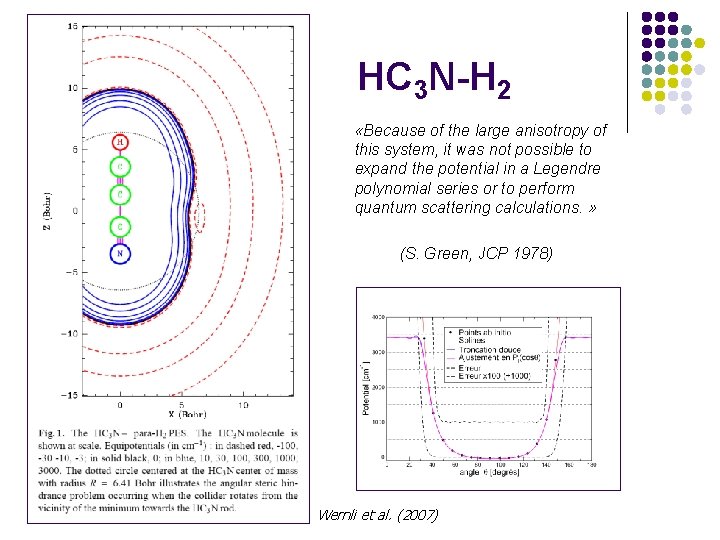
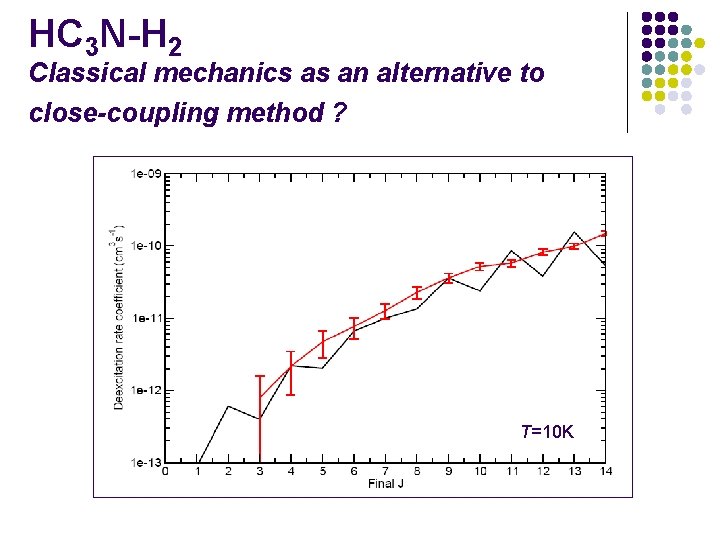
HC 3 N-H 2 «Because of the large anisotropy of this system, it was not possible to expand the potential in a Legendre polynomial series or to perform quantum scattering calculations. » (S. Green, JCP 1978) Wernli et al. (2007)

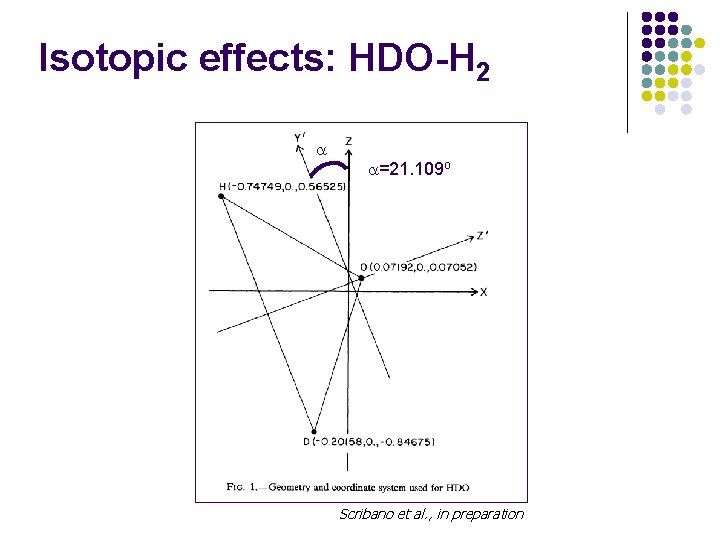
Isotopic effects: HDO-H 2 =21. 109 o Scribano et al. , in preparation

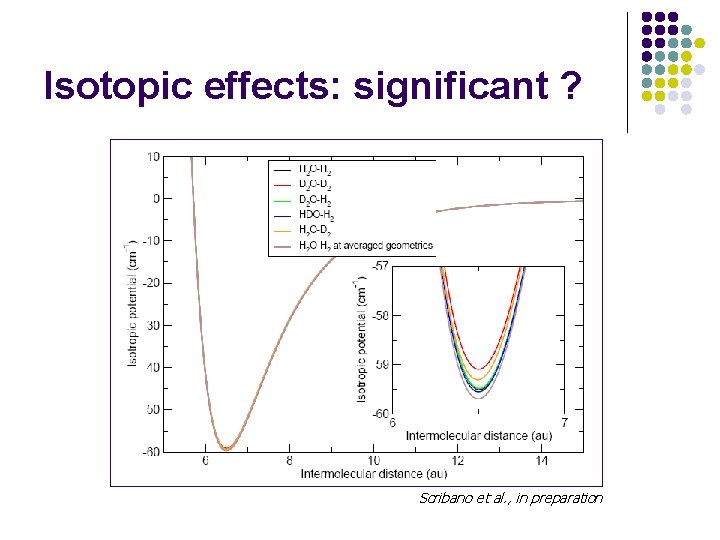
Isotopic effects: significant ? Scribano et al. , in preparation

2. Scattering calculations

Close-coupling approach Schrödinger (time independent) equation + Born-Oppenheimer PES Total wavefunction Cross section and S-matrix S 2 = transition probability

Classical approach Hamilton’s equations Cross section and impact parameter Statistical error Rate coefficient (canonical Monte-Carlo)

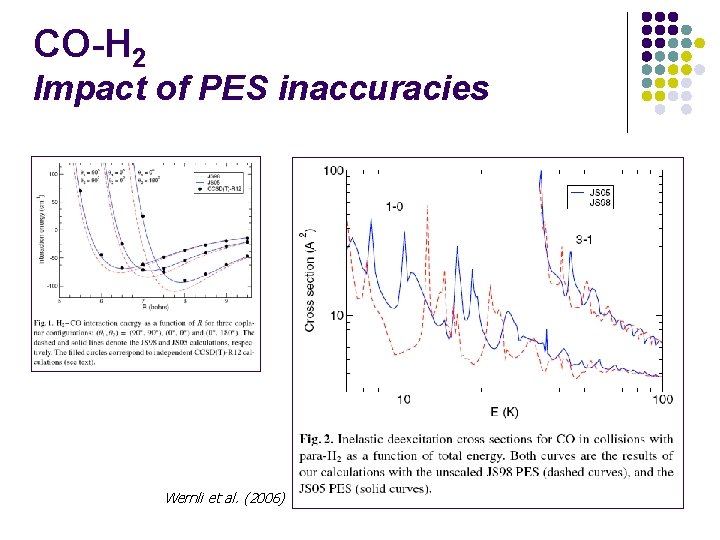
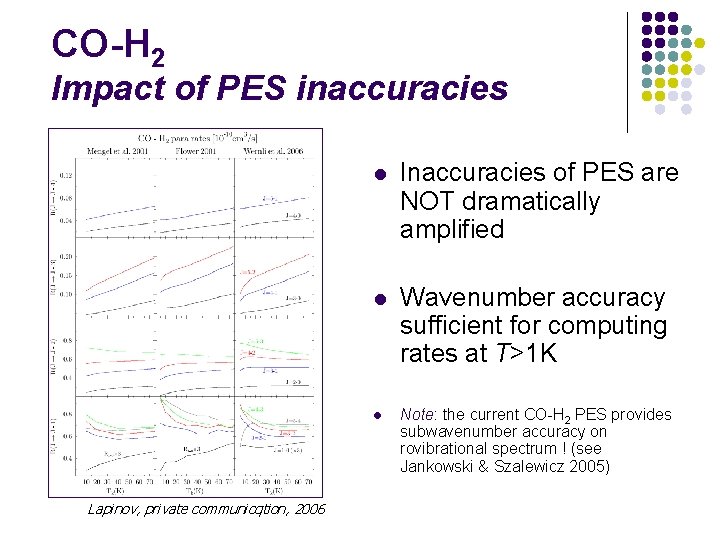
CO-H 2 Impact of PES inaccuracies Wernli et al. (2006)

CO-H 2 Impact of PES inaccuracies l Inaccuracies of PES are NOT dramatically amplified l Wavenumber accuracy sufficient for computing rates at T>1 K l Lapinov, private communicqtion, 2006 Note: the current CO-H 2 PES provides subwavenumber accuracy on rovibrational spectrum ! (see Jankowski & Szalewicz 2005)

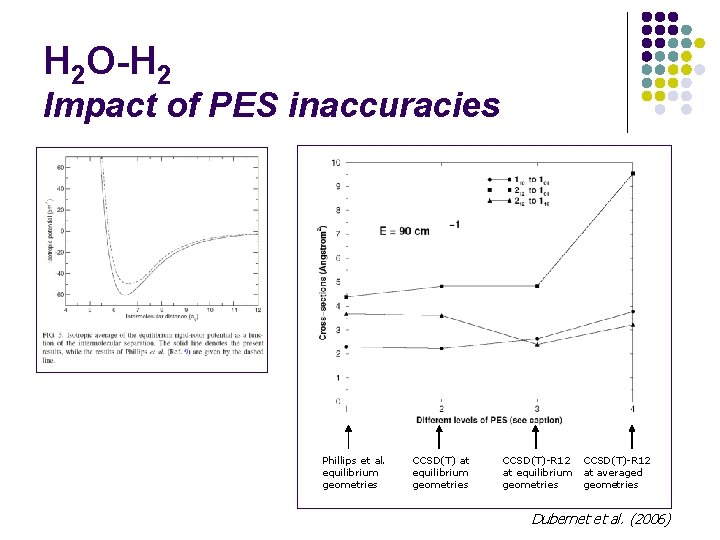
H 2 O-H 2 Impact of PES inaccuracies Phillips et al. equilibrium geometries CCSD(T) at equilibrium geometries CCSD(T)-R 12 at averaged geometries Dubernet et al. (2006)

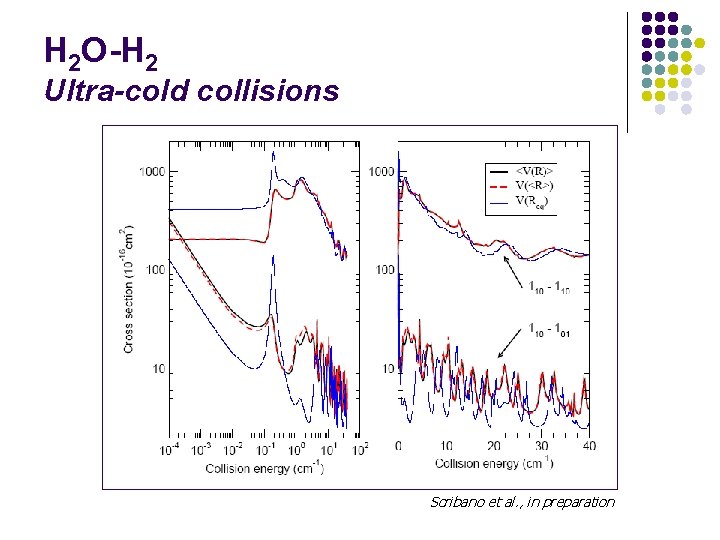
H 2 O-H 2 Ultra-cold collisions Scribano et al. , in preparation

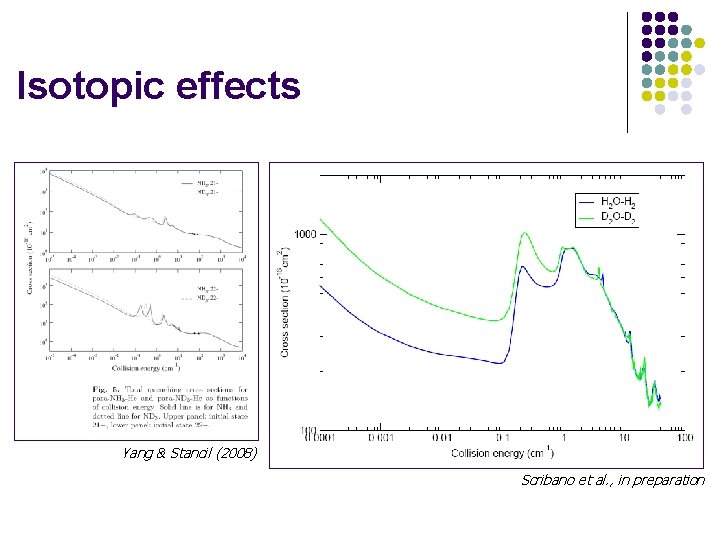
Isotopic effects Yang & Stancil (2008) Scribano et al. , in preparation

HC 3 N-H 2 Classical mechanics as an alternative to close-coupling method ? T=10 K

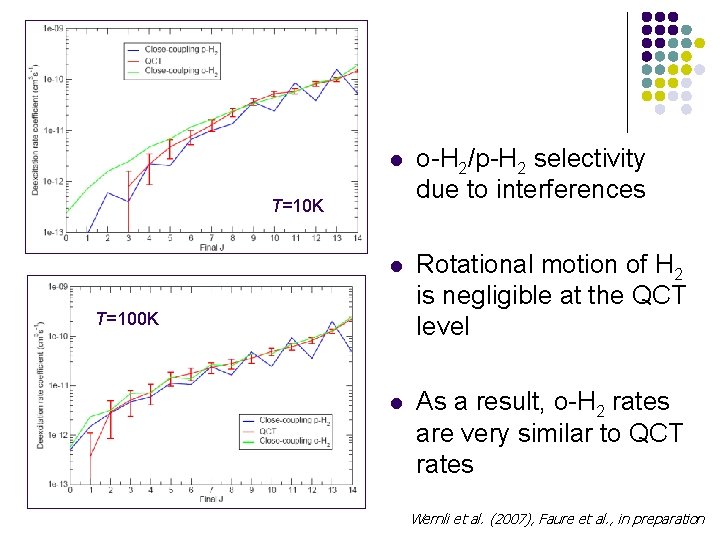
l o-H 2/p-H 2 selectivity due to interferences l Rotational motion of H 2 is negligible at the QCT level l As a result, o-H 2 rates are very similar to QCT rates T=10 K T=100 K Wernli et al. (2007), Faure et al. , in preparation

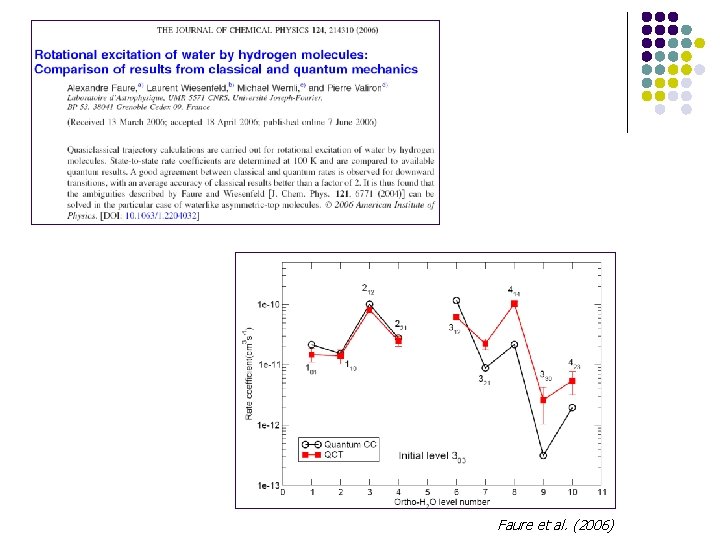
Faure et al. (2006)

Experimental tests l Total (elastic + inelastic) cross sections l Differential cross sections l Pressure broadening cross sections l Second virial coefficients l Rovibrational spectrum of vd. W complexes

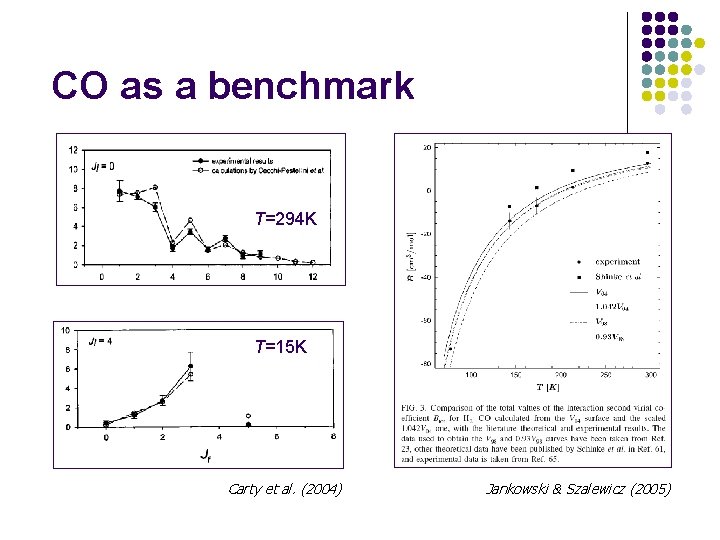
CO as a benchmark T=294 K T=15 K Carty et al. (2004) Jankowski & Szalewicz (2005)

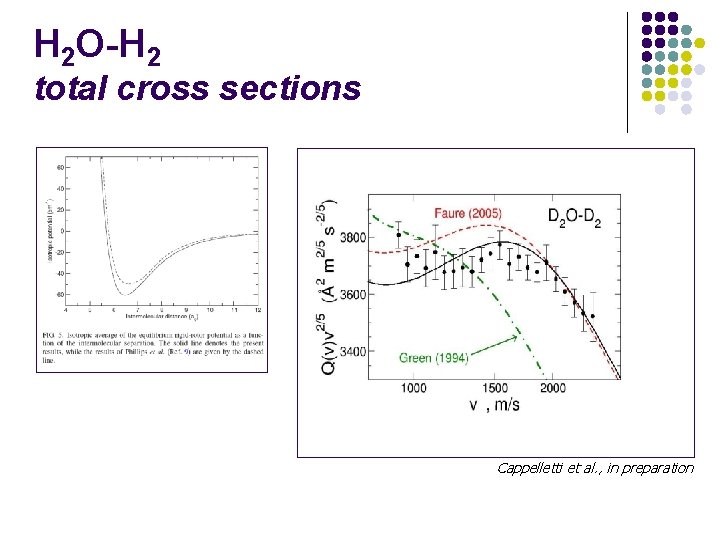
H 2 O-H 2 total cross sections Cappelletti et al. , in preparation

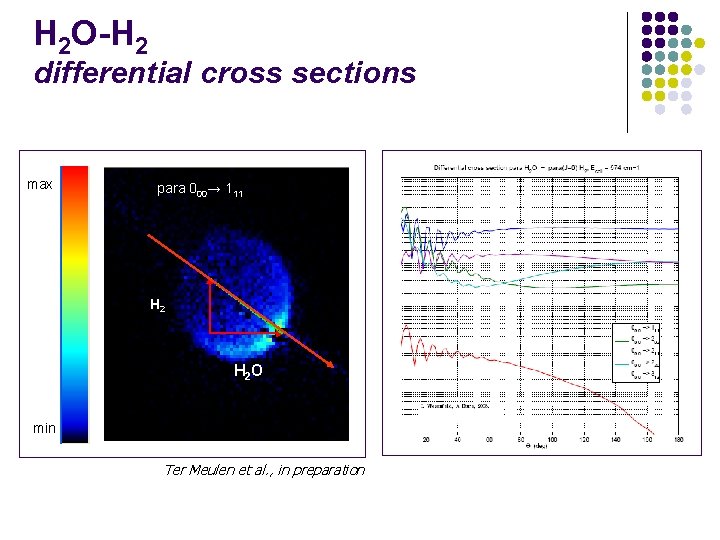
H 2 O-H 2 differential cross sections max para 000→ 111 H 2 O min Ter Meulen et al. , in preparation

Conclusions l Recent advances on inelastic collisions l l l PES l Ab initio: CCSD(T) + CBS/R 12 l Fitting: Monte-Carlo estimator Cross section and rates l Wavenumber accuracy of PES is required but sufficient l Success and limits of classical approximation Future directions l l « Large » polyatomic species (e. g. CH 3 OCH 3) Vibrational excitation, in particular « floppy » modes