Potencias y raz cuadrada 1 Potencias de exponente

Potencias y raíz cuadrada 1 Potencias de exponente natural mayor que 1 En la expresión 3 · 3 · 3 · 3 · 3 se repite el mismo factor 14 veces. Para abreviar escribimos: 3 · 3 · 3 · 3 · 3 = 314 es una potencia de base 3 y exponente 14: 314 La base es el factor que se repite. 314 = 4. 782. 969 exponente base 234 = 23 · 23 El exponente indica el número de veces que se repite 23 cuatro veces Las potencias de exponente 2 se llaman cuadrados: 52 es el cuadrado de 5. Las potencias de exponente 3 se llaman cubos: 103 es el cubo de 10. 103 = 1000 Otros ejemplos: (a) 2 · 2 · 2 · 2 = 210 = 1. 024 (b) 65 = 6 · 6 · 6 IMAGEN FINAL

Potencias y raíz cuadrada 2 Potencias de base un número negativo Si la base es un número negativo: (– 3) · (– 3) = (– 3)4 = 81 Un número positivo. Pero Un número negativo. (– 3) · (– 3) = (– 3)5 = – 243 Si el exponente es 4, resulta un número positivo Recuerda que (–) · (–) = + porque hay un número par de signos negativos. y que (–) · (–) = (–) Si el exponente es 5, resulta un número negativo porque hay un número impar de signos negativos. ¡Cuidado! (– 5)2 = 25, pero En general: – 52 = – 25 Las potencias de base negativa y exponente par son positivas. Las potencias de base negativa y exponente impar son negativas. Otros ejemplos: Son positivas: (a) (– 2)6 = 64 (b) (– 4)2 = 16 (c) (– 1)·(– 1)·(– 1) = (– 1)8 = 1 Son negativas: (a) (– 2)5 = – 32 (b) (– 4)3= – 64 (c) (– 1)·(– 1 )·(– 1) = (– 1)7 = – 1 IMAGEN FINAL

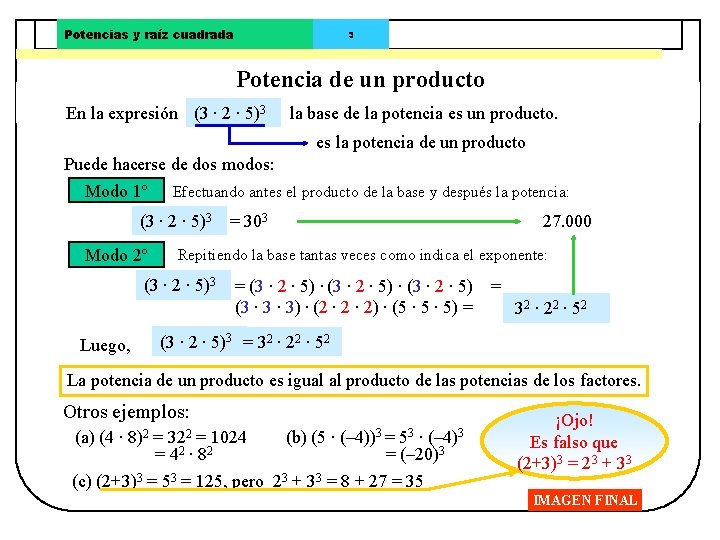
Potencias y raíz cuadrada 3 Potencia de un producto En la expresión (3 · 2 · 5)3 la base de la potencia es un producto. es la potencia de un producto Puede hacerse de dos modos: Modo 1º Efectuando antes el producto de la base y después la potencia: (3 · 2 · 5)3 = 303 Modo 2º Repitiendo la base tantas veces como indica el exponente: (3 · 2 · 5)3 Luego, 27. 000 = (3 · 2 · 5) · (3 · 2 · 5) (3 · 3) · (2 · 2) · (5 · 5) = = 32 · 22 · 52 (3 · 2 · 5)3 = 32 · 22 · 52 La potencia de un producto es igual al producto de las potencias de los factores. Otros ejemplos: (a) (4 · 8)2 = 322 = 1024 = 42 · 82 (b) (5 · (– 4))3 = 53 · (– 4)3 (– 20)3 = (c) (2+3)3 = 53 = 125, pero 23 + 33 = 8 + 27 = 35 ¡Ojo! Es falso que (2+3)3 = 23 + 33 IMAGEN FINAL

Potencias y raíz cuadrada 4 Potencia de un cociente En la expresión (32 : 8)3 la base de la potencia es un cociente. es la potencia de un cociente Puede hacerse de dos modos: Modo 1º Efectuando primero el cociente de la base y después la potencia: (32 : 8)3 = 43 Modo 2º 64 Repitiendo la base tantas veces como indica el exponente: (32 : 8)3 Luego, (32 : 8)3 = 323 : 83 Otros ejemplos: La potencia de un cociente es igual al cociente de la potencia del dividendo y de la potencia del divisor. (a) (6 : 2)4 = 34 = 81 (b) [(– 15) : 3)3 = (– 5)3 = – 125 O también: (c) (32 – 8)3 = 243 = 13824, pero 323 – 83 = 32768 – 512 = 32256 ¡Ojo! Es falso que (32 – 8)3 = 323 – 83 IMAGEN FINAL

Potencias y raíz cuadrada 5 Producto de potencias de la misma base Los factores del producto 42 · 45 · 43 son potencias que tienen la misma base. Es un producto de potencias de la misma base Puede hacerse de dos modos: Modo 1º Directamente, multiplicando: 42 · 45 · 43 = 16 · 1024 · 64 = 1048576 Modo 2º Escribiendo cada potencia como producto y agrupar después: 42 · 45 · 43 Luego, = (4 · 4) · (4 · 4) = 42 · 45 · 43 = 42+5+3 = 410 2, 5 y 3 factores El producto de potencias de la misma basees igual a una potencia con la misma base, y de exponente la suma de los exponentes de los factores. Ejemplos: – 2 = (– 2)1 o 61 = 6 1. (– 2)4 · (– 2)2 = (– 2)4+1+2 = (– 2)7 = – 128, utilizando la propiedad vista. También es igual a: 16 · (– 2) · 4 = – 128, haciendo los productos de las potencias. 2. En forma de potencia, la expresión: (a) 9 · (– 3)3 · (– 3) = (– 3)2 · (– 3)3 · (– 3) = (– 3)6 Igualmente: (b) 16 · (– 2)3 = (– 2)4 · (– 2)3 = (– 2)7 IMAGEN FINAL

Potencias y raíz cuadrada 6 Cociente de potencias de la misma base El dividendo y el divisor de 65 : 63 son potencias de la misma base Puede hacerse de dos modos: Modo 1º Calculando las potencias y dividiendo: Modo 2º Es un cociente de potencias de la misma base Desarrollando las potencias y simplificando: 65 : 63 = 65– 3 65 : 63 El cociente de dos potencias de la misma base es una potencia con la misma base, y con exponente la diferencia entre los exponentes del dividendo y del divisor. Caso: El cociente 54 : 54 = 1 Pero si aplicamos la propiedad 54 : 54 = 54– 4 = 50 Ejercicio: Escribe en forma de potencia: (a) 27 : 24 = 27– 4 = 23 Se admite que: 50 = 1; (– 7)0 = 1 (b) (– 5)6 : (– 5)3 = (– 5)6 -3 = (– 5)3 IMAGEN FINAL

Potencias y raíz cuadrada 7 Potencia de una potencia La expresión (52)4 es una potencia cuya base es otra potencia. Puede hacerse de dos modos: Se llama potencia de una potencia Modo 1º Directamente, haciendo la potencia de la potencia: (52)4 = (25)4 = 390625 Modo 2º Escribiendo como producto de potencias y agrupar después: (52)4 = 52 · 4 (5 2)4 = 52 · 52 = 52+2+2+2 = 52 · 4 = 58 La potencia de una potenciaes igual a otra potencia con la misma base, y de exponente el producto de exponentes. Ejercicios 1. Calcula: [(– 2)4]2 2. Calcula: [(35)4]2 = 35· 4· 2 = 340 3. Calcula: {[(– 1)3]9}7 = (– 1)3· 9· 7 = (– 1)189 = – 1 = (– 2)4· 2 = (– 2)8 = 64 340 es un número enorme: tiene 20 cifras. IMAGEN FINAL

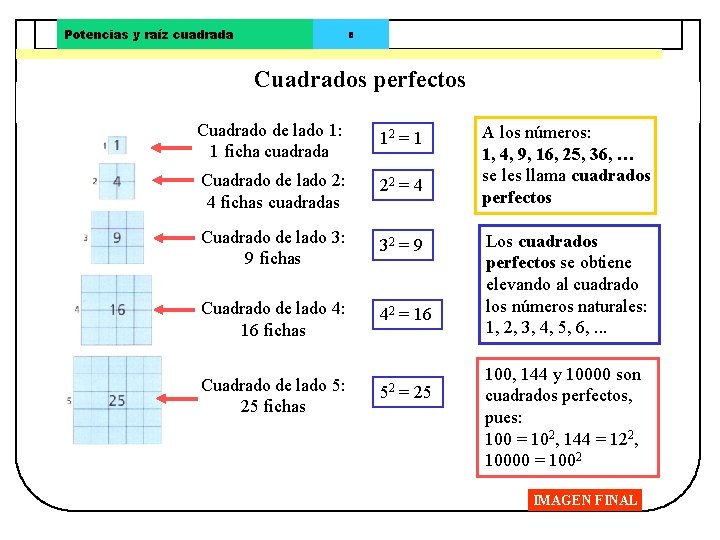
Potencias y raíz cuadrada 8 Cuadrados perfectos Cuadrado de lado 1: 1 ficha cuadrada 12 = 1 Cuadrado de lado 2: 4 fichas cuadradas 22 = 4 Cuadrado de lado 3: 9 fichas 32 = 9 Cuadrado de lado 4: 16 fichas 42 = 16 Cuadrado de lado 5: 25 fichas 52 = 25 A los números: 1, 4, 9, 16, 25, 36, … se les llama cuadrados perfectos Los cuadrados perfectos se obtiene elevando al cuadrado los números naturales: 1, 2, 3, 4, 5, 6, . . . 100, 144 y 10000 son cuadrados perfectos, pues: 100 = 102, 144 = 122, 10000 = 1002 IMAGEN FINAL

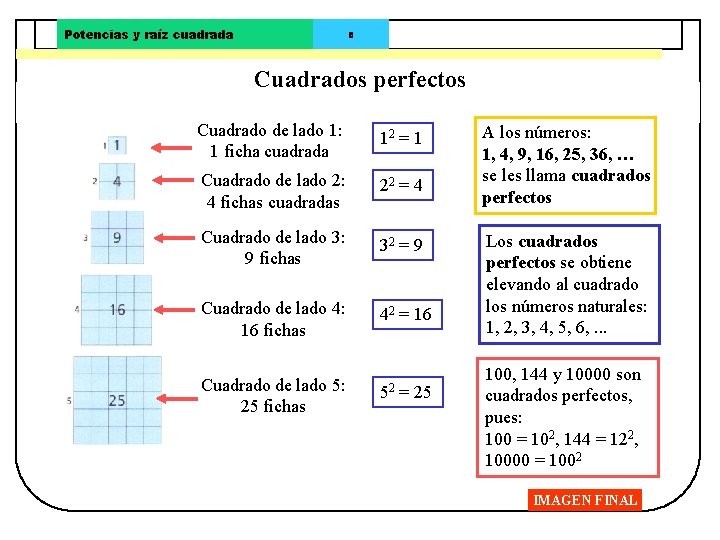
Potencias y raíz cuadrada 8 Cuadrados perfectos Cuadrado de lado 1: 1 ficha cuadrada 12 = 1 Cuadrado de lado 2: 4 fichas cuadradas 22 = 4 Cuadrado de lado 3: 9 fichas 32 = 9 Cuadrado de lado 4: 16 fichas 42 = 16 Cuadrado de lado 5: 25 fichas 52 = 25 A los números: 1, 4, 9, 16, 25, 36, … se les llama cuadrados perfectos Los cuadrados perfectos se obtiene elevando al cuadrado los números naturales: 1, 2, 3, 4, 5, 6, . . . 100, 144 y 10000 son cuadrados perfectos, pues: 100 = 102, 144 = 122, 10000 = 1002 IMAGEN FINAL

Potencias y raíz cuadrada 9 Raíz cuadrada exacta Sabemos que los números: 1, 4, 9, 16, 25, 36, … son los cuadrados perfectos de los números naturales 1, 2, 3, 4, 5, 6, . . . También se dice que 1, 2, 3, 4, 5, 6, … son la raíz cuadradade los números: 1, 4, 9, 16, 25, 36, … respectivamente. Se escribe así: Raíz cuadrada exactade número es otro número que elevado al cuadrado es igual al número dado. La raíz cuadrada es la operación opuesta de elevar al cuadrado Ejemplos: 1º. Como 100 = 102, se cumple que 2º. 3º. Ten en cuenta: Como 36 = 62 = (– 6)2, 6 y – 6 son raíces cuadradas de 36. IMAGEN FINAL

Potencias y raíz cuadrada 9 Raíz cuadrada exacta Sabemos que los números: 1, 4, 9, 16, 25, 36, … son los cuadrados perfectos de los números naturales 1, 2, 3, 4, 5, 6, . . . También se dice que 1, 2, 3, 4, 5, 6, … son la raíz cuadradade los números: 1, 4, 9, 16, 25, 36, … respectivamente. Se escribe así: Raíz cuadrada exactade número es otro número que elevado al cuadrado es igual al número dado. La raíz cuadrada es la operación opuesta de elevar al cuadrado Ejemplos: 1º. Como 100 = 102, se cumple que 2º. 3º. Ten en cuenta: Como 36 = 62 = (– 6)2, 6 y – 6 son raíces cuadradas de 36. IMAGEN FINAL

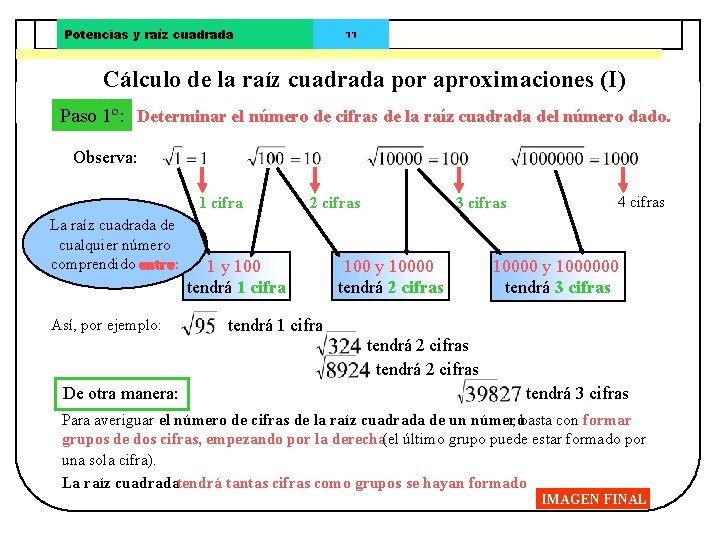
Potencias y raíz cuadrada 11 Cálculo de la raíz cuadrada por aproximaciones (I) Paso 1º: Determinar el número de cifras de la raíz cuadrada del número dado. Observa: 1 cifra La raíz cuadrada de cualquier número comprendido entre: Así, por ejemplo: 2 cifras 1 y 100 tendrá 1 cifra 3 cifras 100 y 10000 tendrá 2 cifras 4 cifras 10000 y 1000000 tendrá 3 cifras tendrá 1 cifra tendrá 2 cifras De otra manera: tendrá 3 cifras Para averiguar el número de cifras de la raíz cuadrada de un número , basta con formar grupos de dos cifras, empezando por la derecha(el último grupo puede estar formado por una sola cifra). La raíz cuadradatendrá tantas cifras como grupos se hayan formado. IMAGEN FINAL

Potencias y raíz cuadrada 12 Números 2001 - Matemáticas 1º ESO Cálculo de la raíz cuadrada por aproximaciones (II) Paso 2º: Buscar dos cuadrados perfectos entre los cuales esté el número dado. Tendrá 3 cifras: será un número entre 100 y 1. 000. Por ejemplo: Como 100 2 = 10. 000 < 12. 824 < 40. 000 = 200 2 · Para determinar la cifra de las decenas calculamos los cuadrados de 110, 120, 130, etc. Como 110 2 = 12. 100 y 120 2 = 14. 400, 12. 100 < 12. 834 < 14. 400 · Para determinar la cifra de las unidades calculamos los cuadrados de 111, 112, 113, etc. Como: 111 2 = 12. 321 < 12. 834, 112 2 = 12. 544 < 12. 834, 113 2 = 12. 769 < 12. 834, 114 2 = 12. 996 > 12. 834 Luego, (con resto 55, pues 12. 824 – 1132 = 55). Otro ejemplo: Calcula por aproximación (tendrá 2 cifras) Probamos con 402, 502, 602, etc. Luego, 402 = 1600 502 = 2500 3456 602 = 3600 Haciendo los cuadrados de 51, 52, …, se observa que: IMAGEN FINAL

Potencias y raíz cuadrada 13 Regla para el cálculo de la raíz cuadrada (I) La regla tradicional para el cálculo de la raíz entera de un número requiere una organización específica que indicamos a continuación. Para calcular la raíz de un número, por ejemplo 1º. Se divide el radicando en grupos de dos cifras, empezando por la derecha. 2º. Se trazan líneas que faciliten la aplicación de la regla. 3º. Esta regla tiene pasos parecidos a los empleados en la división; también se restará y se bajarán cifras, pero en este caso por grupos de dos 4º. El último paso consistirá en la comprobación: en la prueba de la radicación: Lugar para la raíz Espacio para operar Espacio para pruebas y tanteos resto 118527 = (raíz)2 + resto IMAGEN FINAL

Potencias y raíz cuadrada 14 Regla para el cálculo de la raíz cuadrada (II) Calculemos 2º. Se hace el cuadrado de 3 y se resta al primer grupo: a 11 3º. Se baja el segundo grupo de cifras: 85 5º. Se resta 285 – 256. 7º. Se baja el tercer grupo de cifras: 27 3 44 – 9 22 85 – 2 56 29 27 – 27 36 191 664 · 4 = 256 68 684 · 4 = 2736 9º. Se resta 2927 – 2736 El número 191 es el resto de la raíz. Por tanto, 11º. Se hace la prueba: 3442 + 191 = 118336 + 191 = 118527 1º. Se calcula la raíz cuadrada del primer grupo de cifras: de 11. Es 3 4º. Se toma el doble de 3 que es 6: a su izquierda se coloca otro número (6 d), de modo que (6 d·d), dé un número lo más próximo a 285, sin superarlo Ese número es 4: 64 · 4 = 256 6º. El número d (4) se coloca a la derecha del 3: 34 8º. Se toma el doble de 34, 68, y se procede como en 4º Ese nuevo d vale también 4. Se multiplica: 684 · 4 = 2736. 10º. La cifra 4 se coloca a la derecha de 34: 3 4 4 IMAGEN FINAL

Potencias y raíz cuadrada 16 Resolución de problemas Problema: Se colocan fichas en filas y en columnas de modo que formen el mayor cuadrado posible. Quedan sin colocar 43 fichas. Si se tuviera 22 fichas más se podría formar un cuadrado sin que sobrara ninguna ficha. ¿Cuántas fichas hay? Primero: Tantear para comprender mejor Observamos que el número de fichas debe ser un cuadrado perfecto más 43 ( fichas sobrantes). Si ese número fuese 28, se tendría: 282 + 43 = 784 + 43 = 827. Sumando a ese número 22 (las fichas que faltan) deberá dar otro cuadrado perfecto. Pero, 827 + 22 = 849 no lo es. Luego no puede haber 827. El número 28 no es válido. Segundo: Hacer un dibujo Con las fichas que sobran y faltan (43 + 22 = 65), completaríamos un cuadrado de lado 1 unidad mayor. Luego 64, que es 65 – 1, es el doble del lado. (Quitamos 1 por que se repite. ) El lado valdrá la mitad de 64: 32. El número de fichas será: 322 + 43 = 1067. Tercero: Sobran 43 Faltan 22 Comprobación. Si a 1067 se le suman 22: 1067 + 22 = 1089, que es igual a 332. IMAGEN FINAL