Polygons triangles and capes Aad Goddijn FIsme TSG






















- Slides: 32

Polygons, triangles and capes Aad Goddijn (FIsme) TSG 34 (FIsme) Freudenthal Institute for Science and Mathematics Education Utrecht University, The Netherlands, A. Goddijn@fi. uu. nl 1

A design for a one day team task • Educational setting • Less known Mathematical content • Design process 2

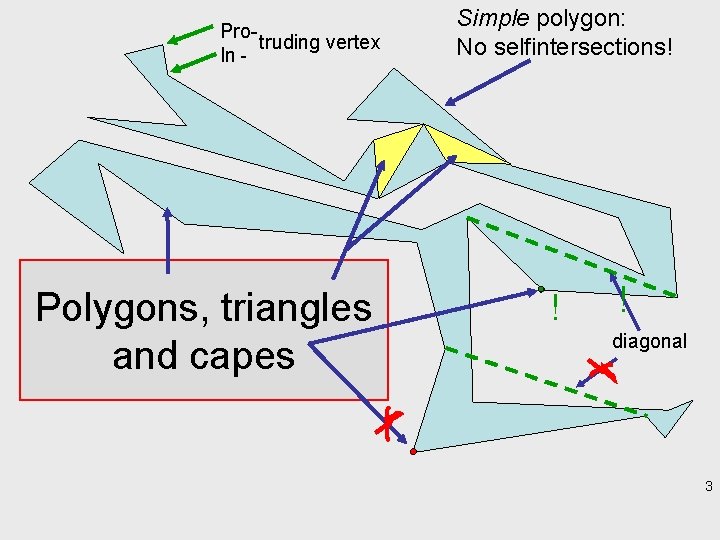
Protruding vertex In - Polygons, triangles and capes Simple polygon: No selfintersections! ! ! diagonal 3

Situation: Math – B day • • Senior Highschool A-lympiad, Math B-day teams of 4 students, no teacher interference One day; 9. 00 – 16. 00 hrs, 27/11/2007. – from initial problem exploration to final essay • Competition + Regular school task • Numbers: (why ? ? , PA) – 180 schools, each 6 -10 teams of 4, about 5000 students (out of 10000) – 118 teams go for competition – 10 winning teams, get a price * *sponsored by TEXAS INSTRUMENTS* 4

Design ‘constraints’ and ideals for the Math B-day assignment • No try-out possible – competition …. . • Teams of students – Debate, argumentation – division of labour • Safe start and adventurious open ending – Regular task + competition; full day – do not send them home in tears • Mathematics as a ‘research’ activity, rounded of by written essay – Guided Reinvention 5

The assignment for november 23, 2007 • 15 pages A 4 • How was it created? 6

Design process timeline • Design team: – 4 Teachers, 1 research mathematician, 2 professional edu-math designers • One-day (24 hours) session of the design team – Wild idea, selecting, exploring, and more • Realisation by 2 team members • Finishing touches by everbody 7

Wild idea • Polyeders of ’s only – Count number of p’s with 10 triangular faces! – Switching edges: Do you get them all by switching? 8

From wild to focus • Debate : – – Exciting! Topology, we never do at school Half-way problems difficult to find Too far away from regular curriculum • Rejected, but: – keep polygons + ’s on board – Related sourcematerial was present in meeting 9

Design team explores mathematics of polygons • Web-source Computational geometry (Ian Garton) – triangulations of polygons stay in center – (Art gallery theorem as a possible application) • Unknown problems for most members! • Design team explores new mathematics like students should do 10

Inspiring van Gogh-like headings at Ian Garton‘s website Ear = Cape 11

Application field: Computational geometry Proofs are not existen ce proofs but Explicit me thods (algo rithms) to fi ‘something nd ’ within a ce rtain time Math B-day ’s choice: - no algorith mic order e stimates 12

End of the day: • Basic exploration of main problems of the subject ready • Rough outline of content • Results : – – possible and impossible problems and solutions, obstacles located tried-out survival hints additional (new) problems • 2 designers promise to write a first version 13

Overview of the assignment • A: Introduction material – definitions, sum of inner angles of simple polygon • C: Basic part: the triangulation theorem – each simple polygon with n sides can be decomposed in n-2 triangles (… a triangulation) • D: Optional part : convex polygons – What is the number of different possible triangulations of a convex n-gon? • (F: Difficult part: The Art Gallery Theorem) – Each simple polygon with n vertices can be guarded by p cameras that are mounted in the vertices, where p is te smallest whole number for which p > n/3 - 1 14

A: Introduction to the field total angular sum of n-gon. Students work: 15

Can’t they do shorter? • Probably! • But: To be handed in: Make a continuous report of your work that is easy to read and can be understood by your fellow students even those who have never heard of simple polygons. 16

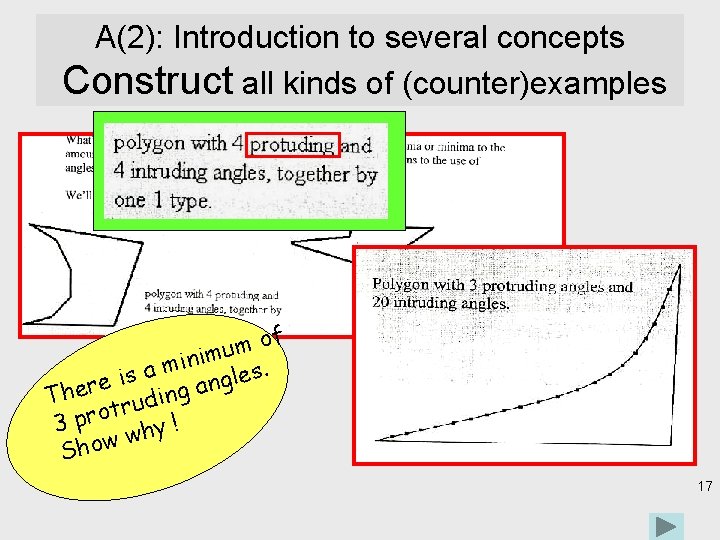
A(2): Introduction to several concepts Construct all kinds of (counter)examples of m u im n i m a s. e s l i g e n Ther ruding a t o r p 3 y! h w Show 17

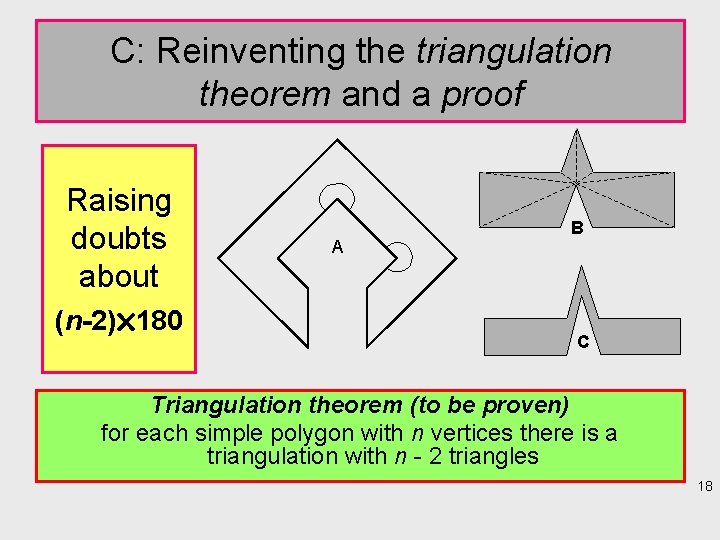
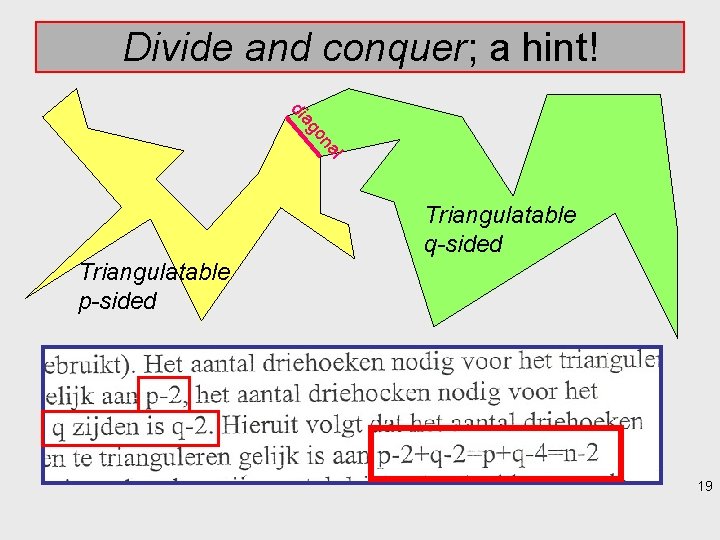
C: Reinventing the triangulation theorem and a proof Raising doubts about (n-2) 180 A B C Triangulation theorem (to be proven) for each simple polygon with n vertices there is a triangulation with n - 2 triangles 18

Divide and conquer; a hint! di l na o ag Triangulatable q-sided Triangulatable p-sided 19

• Part of the design team: proof is ok. • Prediction: Most students will not ask: Is there always a diagonal? • But probably they see the point of it and pick up a suggestion. 20

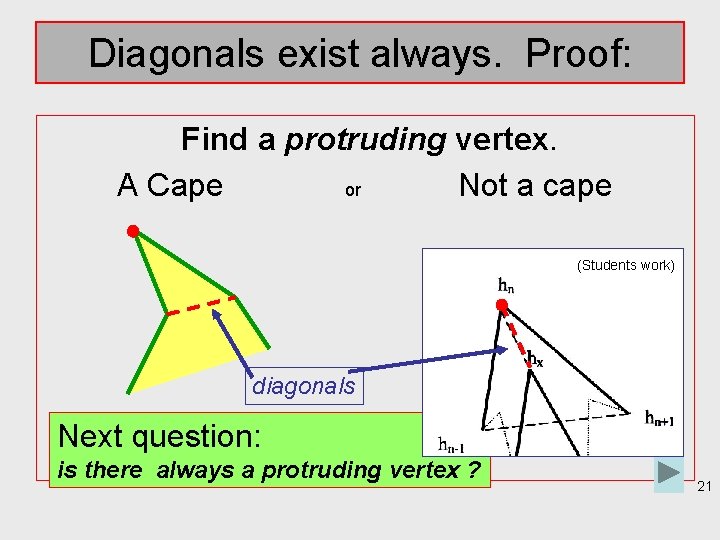
Diagonals exist always. Proof: Find a protruding vertex. A Cape or Not a cape (Students work) diagonals Next question: is there always a protruding vertex ? 21

Guided(? ) reinvention, remarks about • Strong hint about main idea of proof – Main point first: divide and conquer – Students keep overview on the whole story • Proof unrolls in reverse order: – Div+conquer ? ? Diagonal ? ? Protruding vertex ? ? Yes! • In contrast with (axiomatic) deduction: – Polygons -> protruding vertex -> diagonal exist -> divide and conquer -> induction -> theorem -> QED. • Local deduction (Freudenthal) • Explicit proofs rather late in Dutch curriculum, this can be first time – Students show many different levels of retelling the proof-story • Design team explored possible students behavior 22

D: Counting triangulations in the CONVEX case (optional, but recommended) • Problem formulated during design-day: How many different triangulations are possible in a convex 5, 6, 7 -gon? • Initial design motivation: There should be accessible problems for everyone • [Name of this number: Tn ] 23

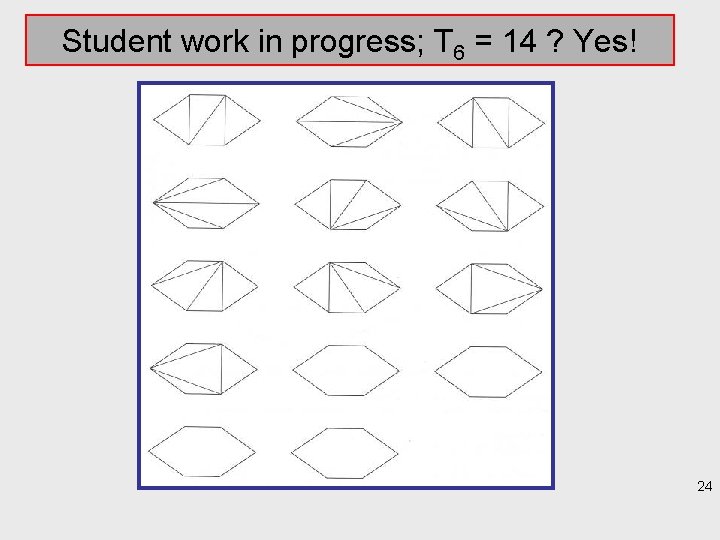
Student work in progress; T 6 = 14 ? Yes! 24

Design team at mathwork again • T 5 = 5, T 6 = 14 • Find T 7 from T 6. • General: – find Tn from earlier Tm’s. • (there is a convolution - recursion formula) • (numbers are the so-called Catalan-numbers) 25

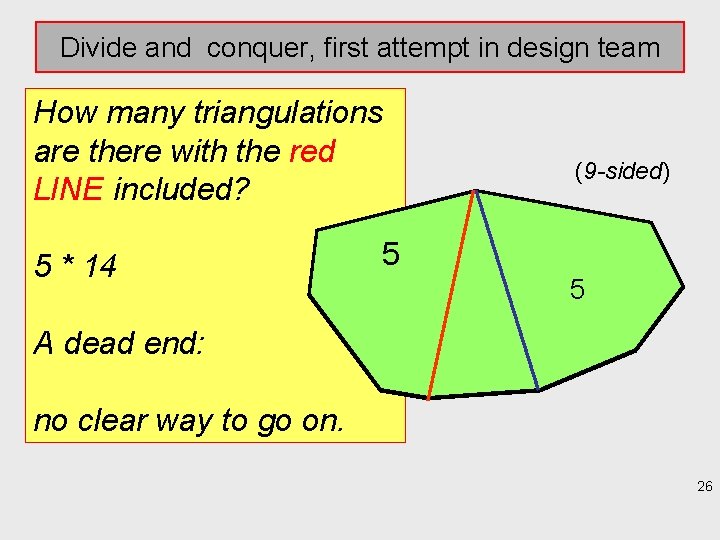
Divide and conquer, first attempt in design team How many triangulations are there with the red LINE included? 5 * 14 14 55 (9 -sided) 14 5 A dead end: no clear way to go on. 26

This Halfway-question is a better hint! How many triangulations are there with the gray triangle included? (10 -sided) 27

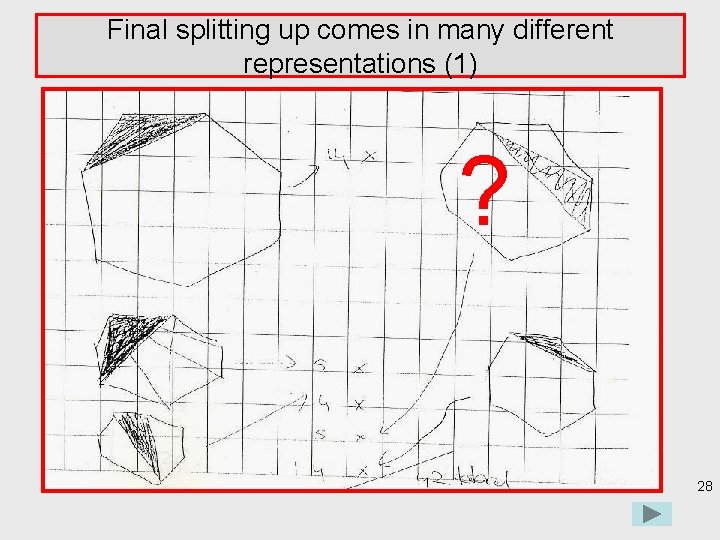
Final splitting up comes in many different representations (1) ? 28

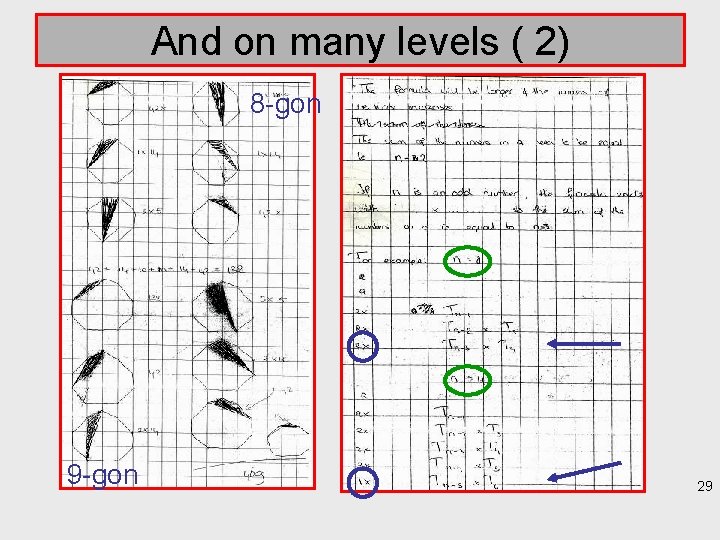
And on many levels ( 2) 8 -gon 9 -gon 29

Final formula found in many styles (3) Difficult spots in process 30

Final formula found in many styles (4) 31

Final conclusion • the hard core of this design process was the mathematical activity of the design team • which is a kind of reinventing of problems and solutions • The resulting guided reinvention in the task – – Prevents some possible disasters helped students exploring a route in the problem field On many different levels … And did not steer them totally from 0 to 100. 32
 Fisme science
Fisme science Poara
Poara Jayeeta saha 3gpp
Jayeeta saha 3gpp Haloch
Haloch Similar congruent shapes
Similar congruent shapes Critical aad
Critical aad Aad/speed program
Aad/speed program El banquero de la resistencia
El banquero de la resistencia Aad hoc
Aad hoc Aad.j
Aad.j Aad van ballegooijen
Aad van ballegooijen Contoh aad
Contoh aad Similar picture
Similar picture Some polygons
Some polygons Isosceles and equilateral triangle
Isosceles and equilateral triangle Cisco unified contact center management portal
Cisco unified contact center management portal Siapg capes
Siapg capes Linha direta capes
Linha direta capes Agradecimentos tese exemplos
Agradecimentos tese exemplos Unist portal
Unist portal Which type of water is generally preferred for shampooing
Which type of water is generally preferred for shampooing Les capes de la terra
Les capes de la terra Peridicos capes
Peridicos capes Element mes abundant al sol
Element mes abundant al sol Bolsa capes ds
Bolsa capes ds Quiz 8-1 angles of polygons and parallelograms
Quiz 8-1 angles of polygons and parallelograms Which of these are concave polygon
Which of these are concave polygon Lesson 11-4 areas of regular polygons
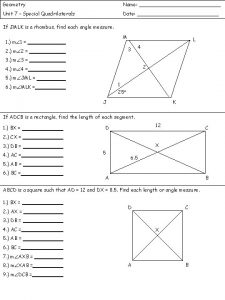
Lesson 11-4 areas of regular polygons Special quadrilaterals
Special quadrilaterals 10-2 developing formulas for circles and regular polygons
10-2 developing formulas for circles and regular polygons Developing formulas for circles and regular polygons
Developing formulas for circles and regular polygons Developing formulas for circles and regular polygons
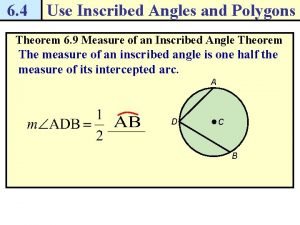
Developing formulas for circles and regular polygons Theorem 6-4
Theorem 6-4