Physics 212 Lecture 21 Slide 1 Music Who

Physics 212 Lecture 21, Slide 1

Music Who is the Artist? A) B) C) D) E) Earth, Wind & Fire War Tower of Power Average White Band Chicago Why? Topic for today = Power

Your Comments “Oh my god that was horrible please don’t make me memorize all that. ” “none of this makes sense please be thurough in lecture” “What significance does Q 2=L/R 2 C have in electrical components? ” “This doesn’t seem conceptually hard but there are tons of new equations and relations between variables. ” “Could you better explain the last lecture and how it leads into this? It looks like its just something you have to stare at for a while but once it clicks then its really easy. I’m having trouble with visualizing the phase diagram and this whole pre lecture was gibberish to me. Not one thing sunk in. ” “i dont see how the transformer relates. . ” 05 We’ll do our best to restate the Big Ideas and give examples Shape of resonance curve (I vs. w) It’s all still based on the phasor diagram! ABSOLUTELY We will connect the two today. . Short review + demo Physics 212 Lecture 21, Slide 3

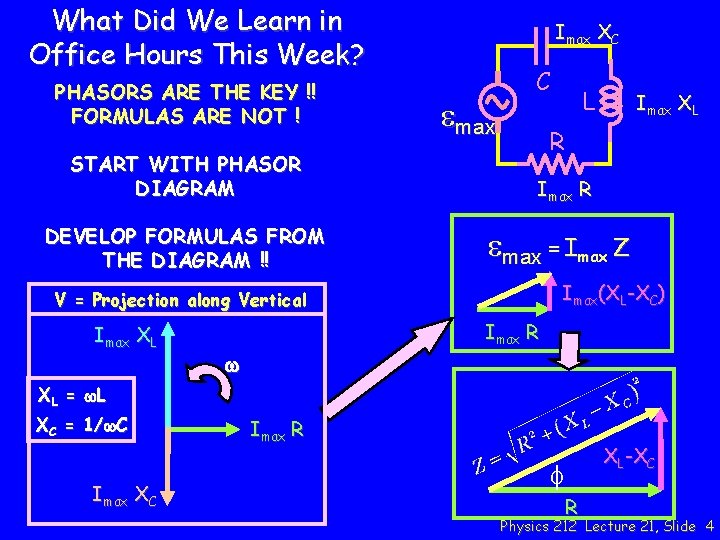
What Did We Learn in Office Hours This Week? PHASORS ARE THE KEY !! FORMULAS ARE NOT ! Imax XC emax C L Imax XL R START WITH PHASOR DIAGRAM Imax R DEVELOP FORMULAS FROM THE DIAGRAM !! emax = Imax Z Imax(XL-XC) V = Projection along Vertical Imax R Imax XL w X L = w. L XC = 1/w. C Imax XC Imax R XL-XC f R Physics 212 Lecture 21, Slide 4

General RLC Example • “Ohms” Law for each element C – NOTE: Good for PEAK values only) – – 07 Vgen = Imax Z VResistor = Imax R Vinductor = Imax XL VCapacitor = Imax XC L R • Typical Problem A generator with peak voltage 15 volts and angular frequency 25 rad/sec is connected in series with an 8 Henry inductor, a 0. 4 m. F capacitor and a 50 ohm resistor. What is the peak current through the circuit? XL R XC Physics 212 Lecture 21, Slide 5

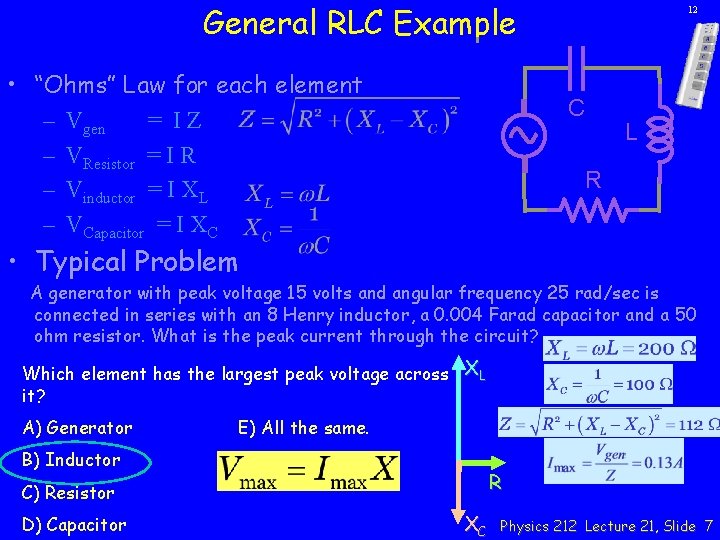
General RLC Example • “Ohms” Law for each element – Vgen = IZ – VResistor = I R – Vinductor = I XL – VCapacitor = I XC 12 C L R • Typical Problem A generator with peak voltage 15 volts and angular frequency 25 rad/sec is connected in series with an 8 Henry inductor, a 0. 004 Farad capacitor and a 50 ohm resistor. What is the peak current through the circuit? Which element has the largest peak voltage across XL it? A) Generator E) All the same. B) Inductor R C) Resistor D) Capacitor XC Physics 212 Lecture 21, Slide 7

General RLC Example 14 • “Ohms” Law for each element – Vgen = IZ – VResistor = I R – Vinductor = I XL – VCapacitor = I XC C L R • Typical Problem A generator with peak voltage 15 volts and angular frequency 25 rad/sec is connected in series with an 8 Henry inductor, a 0. 4 m. F capacitor and a 50 ohm resistor. What is the peak current through the circuit? What happens to the impedance if we decrease the angular frequency to 20 rad/sec? XL XL Z 25 Z 20 A) Z increases R B) Z remains the same C) Z decreases (XL-XC): (200 -100) (160 -125) XC R XC Physics 212 Lecture 21, Slide 8

Resonance Physics 212 Lecture 21, Slide 9

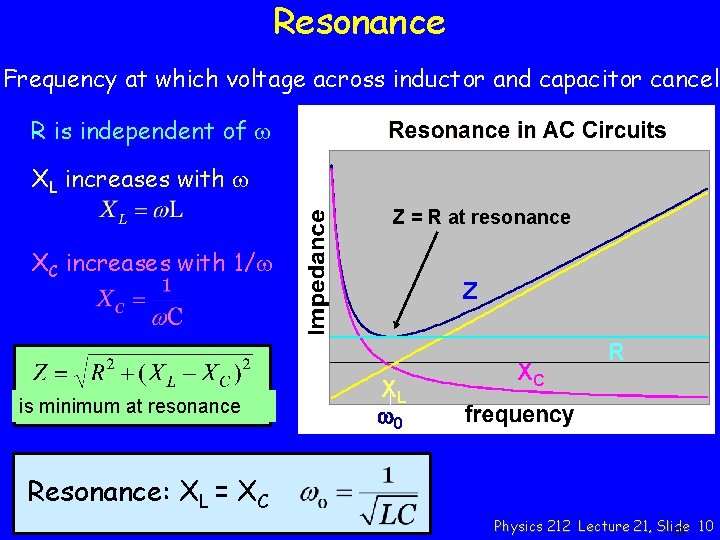
Resonance Frequency at which voltage across inductor and capacitor cancel R is independent of w XL increases with w Z = R at resonance XC increases with 1/w is minimum at resonance Z XL w 0 XC R Resonance: XL = XC Physics 212 Lecture 21, Slide 10 10

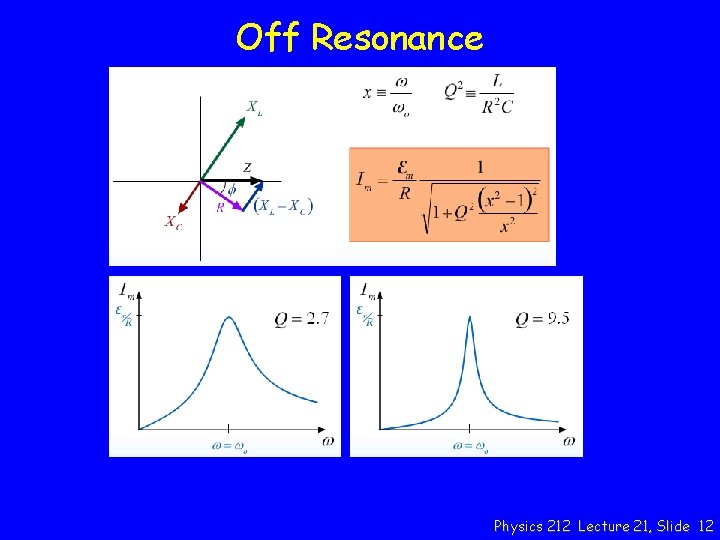
Off Resonance Z In general Umax = max energy stored DU = energy dissipated in one cycle at resonance Physics 212 Lecture 21, Slide 11

Off Resonance Physics 212 Lecture 21, Slide 12

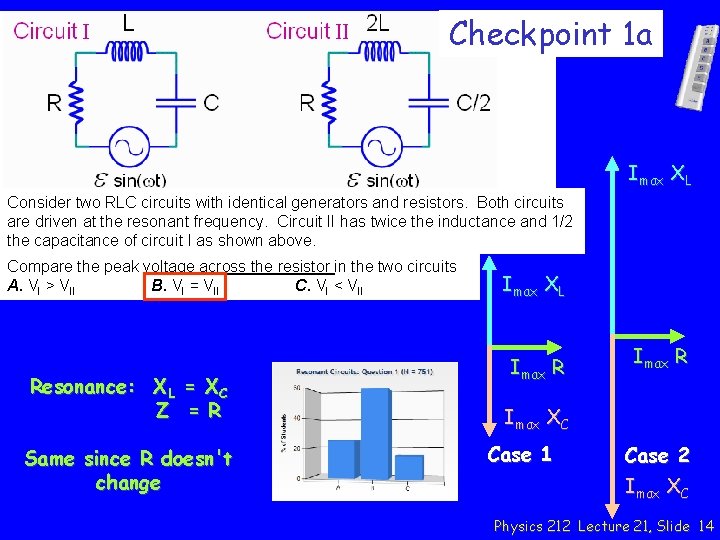
Checkpoint 1 a Consider two RLC circuits with identical generators and resistors. Both circuits are driven at the resonant frequency. Circuit II has twice the inductance and 1/2 the capacitance of circuit I as shown above. Compare the peak voltage across the resistor in the two circuits A. VI > VII B. VI = VII C. VI < VII “Circuit II has twice the impedance and therefore half the peak current and resistor voltage. ” “They would be the same because the circuit has the same impedance. ” “V must be less across the resistor to account for increased voltage in the capacitor and inductor” Physics 212 Lecture 21, Slide 13

Checkpoint 1 a Imax XL Consider two RLC circuits with identical generators and resistors. Both circuits are driven at the resonant frequency. Circuit II has twice the inductance and 1/2 the capacitance of circuit I as shown above. Compare the peak voltage across the resistor in the two circuits A. VI > VII B. VI = VII C. VI < VII Resonance: XL = XC Z = R Same since R doesn't change Imax XL Imax R Imax XC Case 1 Case 2 Imax XC Physics 212 Lecture 21, Slide 14

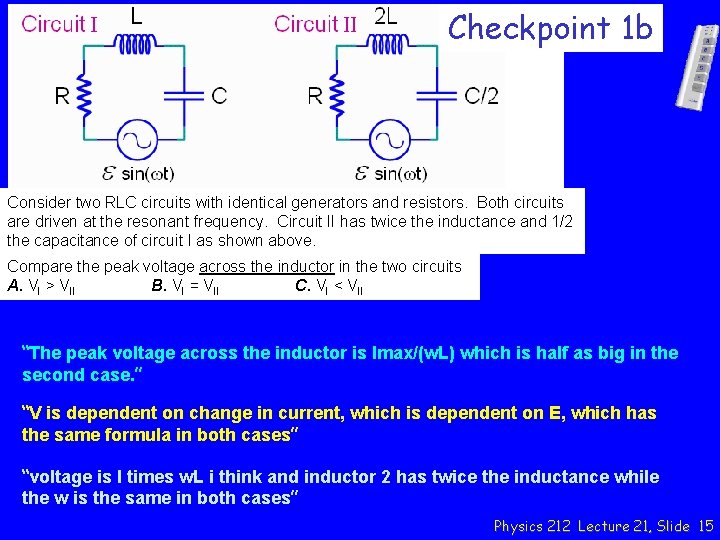
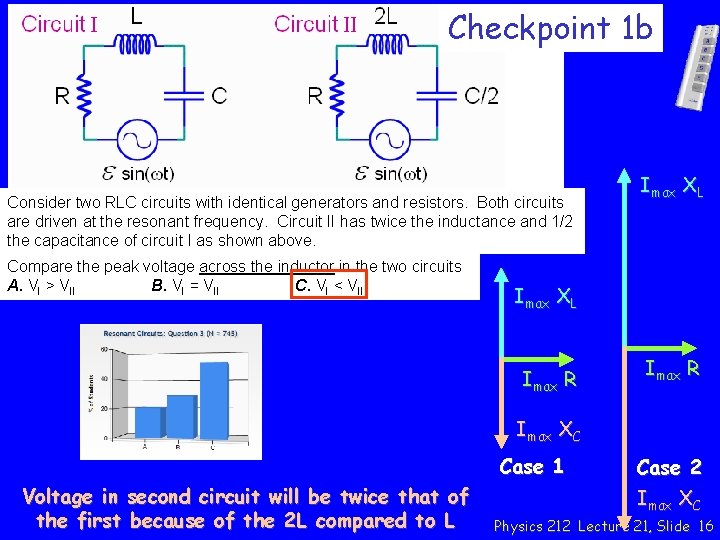
Checkpoint 1 b Consider two RLC circuits with identical generators and resistors. Both circuits are driven at the resonant frequency. Circuit II has twice the inductance and 1/2 the capacitance of circuit I as shown above. Compare the peak voltage across the inductor in the two circuits A. VI > VII B. VI = VII C. VI < VII “The peak voltage across the inductor is Imax/(w. L) which is half as big in the second case. ” “V is dependent on change in current, which is dependent on E, which has the same formula in both cases” “voltage is I times w. L i think and inductor 2 has twice the inductance while the w is the same in both cases” Physics 212 Lecture 21, Slide 15

Checkpoint 1 b Consider two RLC circuits with identical generators and resistors. Both circuits are driven at the resonant frequency. Circuit II has twice the inductance and 1/2 the capacitance of circuit I as shown above. Compare the peak voltage across the inductor in the two circuits A. VI > VII B. VI = VII C. VI < VII Imax XL Imax R Imax XC Case 1 Voltage in second circuit will be twice that of the first because of the 2 L compared to L Case 2 Imax XC Physics 212 Lecture 21, Slide 16

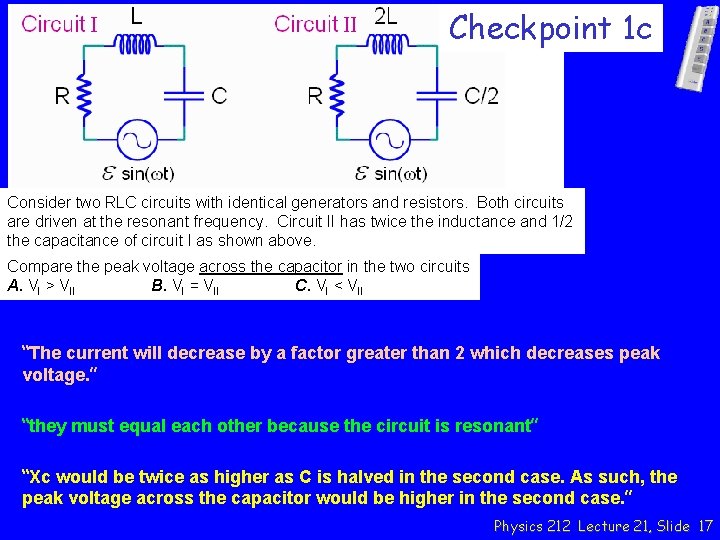
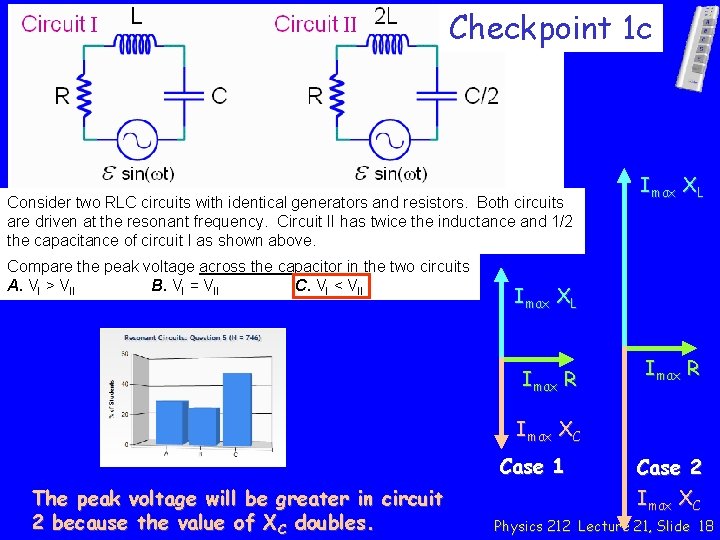
Checkpoint 1 c Consider two RLC circuits with identical generators and resistors. Both circuits are driven at the resonant frequency. Circuit II has twice the inductance and 1/2 the capacitance of circuit I as shown above. Compare the peak voltage across the capacitor in the two circuits A. VI > VII B. VI = VII C. VI < VII “The current will decrease by a factor greater than 2 which decreases peak voltage. ” “they must equal each other because the circuit is resonant” “Xc would be twice as higher as C is halved in the second case. As such, the peak voltage across the capacitor would be higher in the second case. ” Physics 212 Lecture 21, Slide 17

Checkpoint 1 c Consider two RLC circuits with identical generators and resistors. Both circuits are driven at the resonant frequency. Circuit II has twice the inductance and 1/2 the capacitance of circuit I as shown above. Compare the peak voltage across the capacitor in the two circuits A. VI > VII B. VI = VII C. VI < VII Imax XL Imax R Imax XC Case 1 The peak voltage will be greater in circuit 2 because the value of XC doubles. Case 2 Imax XC Physics 212 Lecture 21, Slide 18

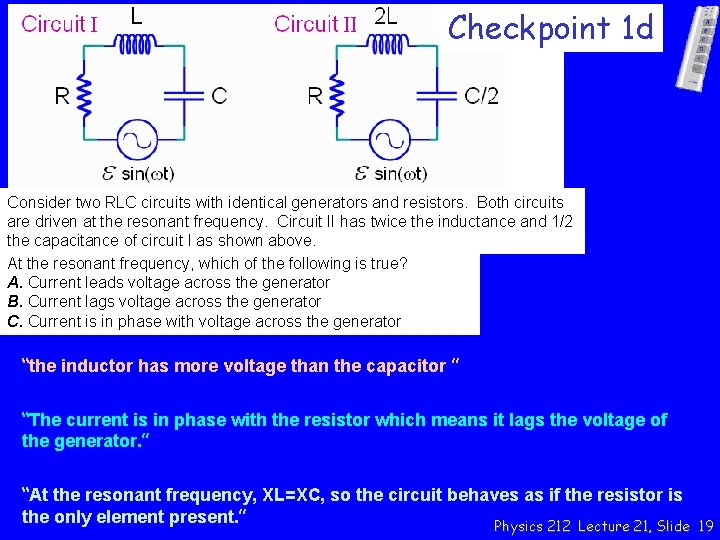
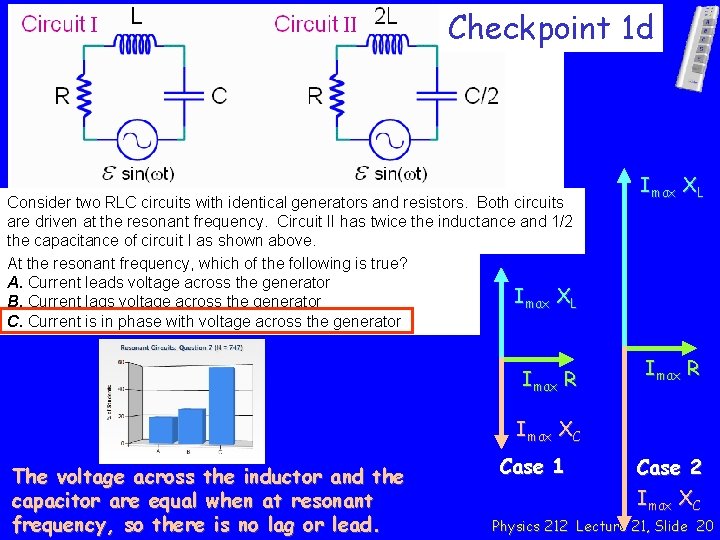
Checkpoint 1 d Consider two RLC circuits with identical generators and resistors. Both circuits are driven at the resonant frequency. Circuit II has twice the inductance and 1/2 the capacitance of circuit I as shown above. At the resonant frequency, which of the following is true? A. Current leads voltage across the generator B. Current lags voltage across the generator C. Current is in phase with voltage across the generator “the inductor has more voltage than the capacitor ” “The current is in phase with the resistor which means it lags the voltage of the generator. ” “At the resonant frequency, XL=XC, so the circuit behaves as if the resistor is the only element present. ” Physics 212 Lecture 21, Slide 19

Checkpoint 1 d Consider two RLC circuits with identical generators and resistors. Both circuits are driven at the resonant frequency. Circuit II has twice the inductance and 1/2 the capacitance of circuit I as shown above. At the resonant frequency, which of the following is true? A. Current leads voltage across the generator Imax XL B. Current lags voltage across the generator C. Current is in phase with voltage across the generator Imax R Imax XL Imax R Imax XC The voltage across the inductor and the capacitor are equal when at resonant frequency, so there is no lag or lead. Case 1 Case 2 Imax XC Physics 212 Lecture 21, Slide 20

Power • P = IV instantaneous always true – Difficult for Generator, Inductor and Capacitor because of phase – Resistor I, V are ALWAYS in phase! C P = IV = I 2 R R • Average Power Inductor and Capacitor = 0 ( Resistor <I 2 R> = <I 2 > R = ½ I 2 peak R RMS = Root Mean Square Ipeak = Irms sqrt(2) L < sinwtcoswt > = 0 ) < I 2 R > = Irms 2 R Physics 212 Lecture 21, Slide 21

Power Line Calculation • If you want to deliver 1500 Watts at 100 Volts over transmission lines w/ resistance of 5 Ohms. How much power is lost in the lines? – Current Delivered: I = P/V = 15 Amps – Loss = IV (on line) = I 2 R = 15*15 * 5 = 1, 125 Watts! • If you deliver 1500 Watts at 10, 000 Volts over the same transmission lines. How much power is lost? – Current Delivered: I = P/V =. 15 Amps – Loss = IV (on line) = I 2 R = 0. 125 Watts DEMO Physics 212 Lecture 21, Slide 22

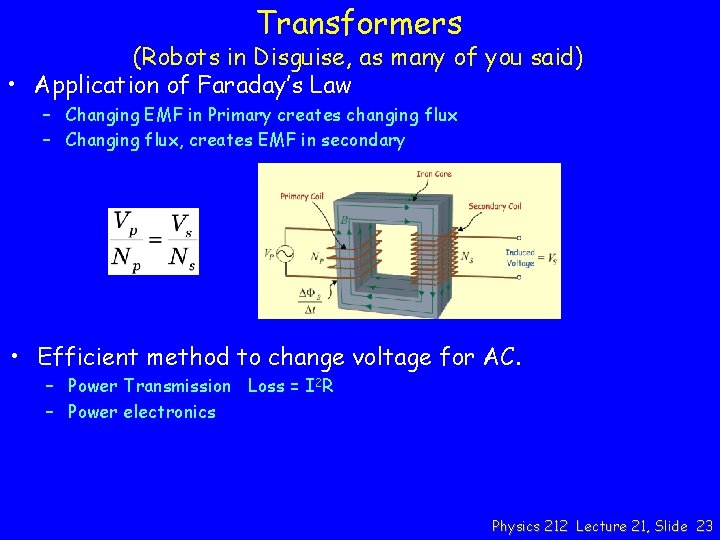
Transformers (Robots in Disguise, as many of you said) • Application of Faraday’s Law – Changing EMF in Primary creates changing flux – Changing flux, creates EMF in secondary • Efficient method to change voltage for AC. – Power Transmission Loss = I 2 R – Power electronics Physics 212 Lecture 21, Slide 23

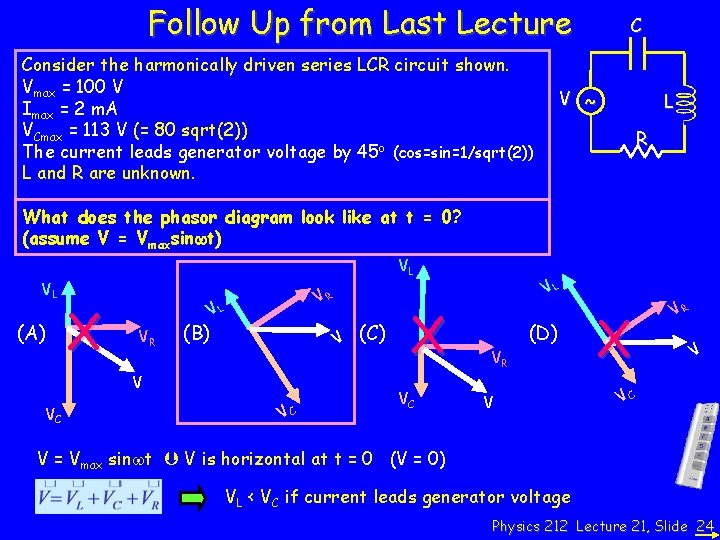
Follow Up from Last Lecture Consider the harmonically driven series LCR circuit shown. Vmax = 100 V Imax = 2 m. A VCmax = 113 V (= 80 sqrt(2)) The current leads generator voltage by 45 o (cos=sin=1/sqrt(2)) L and R are unknown. C V ~ L R What does the phasor diagram look like at t = 0? (assume V = Vmaxsinwt) VL (A) VL X VR VL VR (B) V V VC VC (C) X VC VL VR (D) V X VR V VC V = Vmax sinwt V is horizontal at t = 0 (V = 0) VL < VC if current leads generator voltage Physics 212 Lecture 21, Slide 24

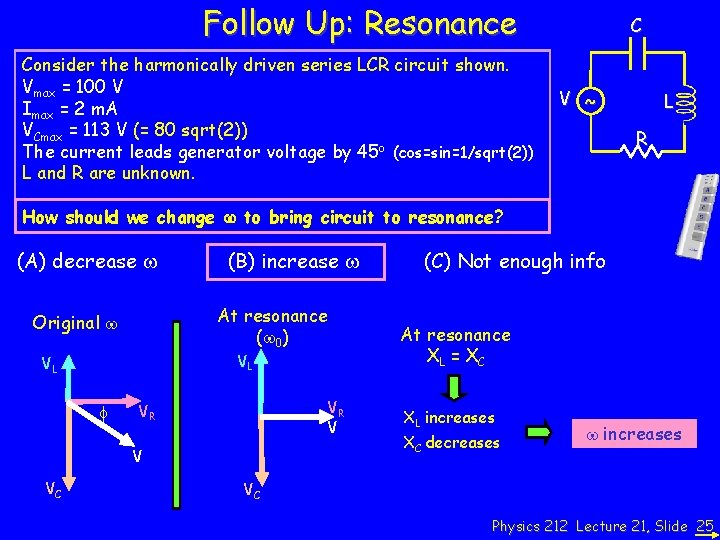
Follow Up: Resonance Consider the harmonically driven series LCR circuit shown. Vmax = 100 V Imax = 2 m. A VCmax = 113 V (= 80 sqrt(2)) The current leads generator voltage by 45 o (cos=sin=1/sqrt(2)) L and R are unknown. C V ~ L R How should we change w to bring circuit to resonance? (A) decrease w (B) increase w At resonance (w 0) Original w VL VL f VR V VC (C) Not enough info At resonance XL = X C XL increases XC decreases w increases VC Physics 212 Lecture 21, Slide 25

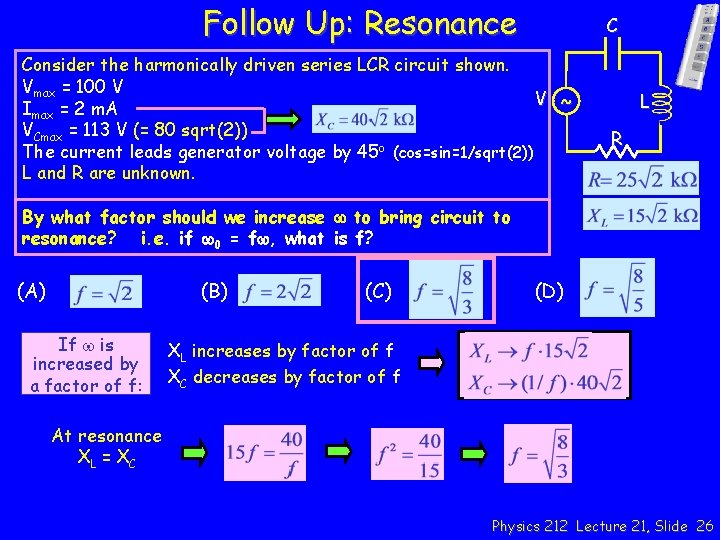
Follow Up: Resonance C Consider the harmonically driven series LCR circuit shown. Vmax = 100 V V ~ Imax = 2 m. A VCmax = 113 V (= 80 sqrt(2)) The current leads generator voltage by 45 o (cos=sin=1/sqrt(2)) L and R are unknown. L R By what factor should we increase w to bring circuit to resonance? i. e. if w 0 = fw, what is f? (A) (B) If w is increased by a factor of f: (C) (D) XL increases by factor of f XC decreases by factor of f At resonance XL = X C Physics 212 Lecture 21, Slide 26

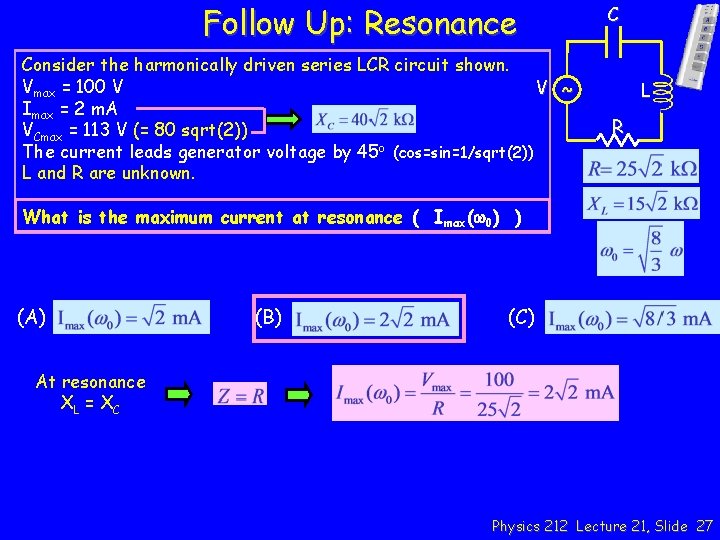
Follow Up: Resonance Consider the harmonically driven series LCR circuit shown. Vmax = 100 V V ~ Imax = 2 m. A VCmax = 113 V (= 80 sqrt(2)) The current leads generator voltage by 45 o (cos=sin=1/sqrt(2)) L and R are unknown. C L R What is the maximum current at resonance ( Imax(w 0) ) (A) (B) (C) At resonance XL = X C Physics 212 Lecture 21, Slide 27