PHYS575CSI655 Introduction to Atmospheric Physics and Chemistry Lecture

PHYS-575/CSI-655 Introduction to Atmospheric Physics and Chemistry Lecture Notes #3 – Part 1: Thermodynamics 1. Thermodynamics Review/Tutorial - Ideal Gas Law - Heat Capacity - 1 st & 2 nd Laws of Thermodynamics - Adiabatic Processes - Energy Transport 2. 3. 4. 5. 6. Hydrostatic Equilibrium Adiabatic Lapse Rate – DRY Adiabatic Lapse Rate - WET Static Stability SLT and the Atmosphere 10/26/2020 1

What is Thermodynamics? Thermodynamics is the study of heat and its transformation from a macroscopic point of view. "Department of Entropy" 10/26/2020 "Now, in the second law of thermodynamics. . . " 2

1. Thermodynamics Tutorial Thermodynamics is the study of heat and its transformation to and from other sources of energy, from a macroscopic point of view. Ø Statistical Mechanics connects thermodynamics to the microscopic world through the statistical description of an ensemble of atoms or molecules that constitute a macroscopic system. Ø The transfer of heat, in turn, is driven by differences in temperature or potential differences associated with chemical reactions. In the interest of crafting a brief tutorial for applications to the atmosphere, I have glossed over some of the finer (but yet important) points of thermodynamics. For more complete treatment: General: Fundamentals of Statistical and Thermal Physics (Mc. Graw-Hill Series in Fundamentals of Physics) by Frederick Reif, 1965. Atmospheric: Atmospheric Thermodynamics, by C. F. Bohren and B. A. Albrecht, Oxford University Press, Oxford, 1998. 10/26/2020 3

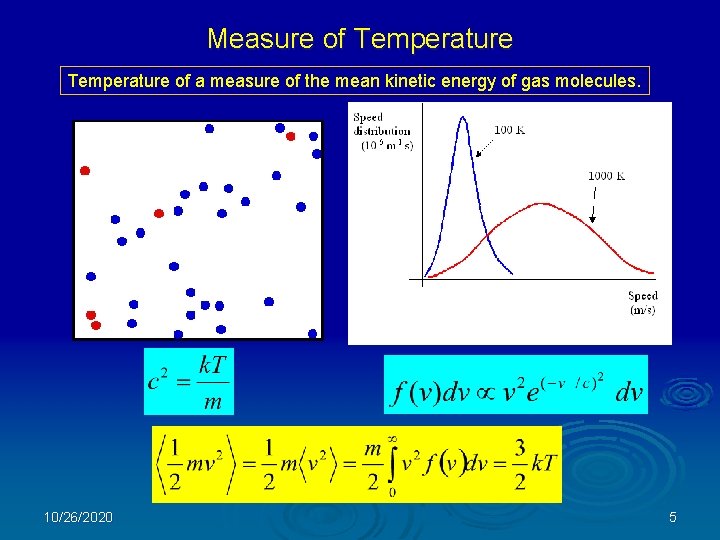
Defining Temperature is a measure of the mean kinetic energy of gas molecules. The temperature of an ideal monatomic gas is related to the average kinetic energy of its atoms as they move. In this animation, the size of helium atoms relative to their spacing is shown to scale under 1950 atmospheres of pressure. These room-temperature atoms have a certain, average speed (slowed down here two trillion fold). 10/26/2020 4

Measure of Temperature of a measure of the mean kinetic energy of gas molecules. 10/26/2020 5

Temperature Scales Temperature is a measure of the random kinetic energy of atoms and/or molecules The Fahrenheit Scale: • we are most familiar with this one • water freezes at 32 degrees F. • water boils at 212 degrees F. • when we cool to the absolute lowest temperature we reach -459 degrees (this is referred to as Absolute Zero) Ø The Celsius Scale: • water freezes at 0 degrees C. • water boils at 100 degrees C. • Absolute Zero is at -273 degrees C. Ø The Kelvin Scale • Absolute Zero is 0 K • a temperature change of 1 degree K is the same as a temperature change of 1 degree C. • water freezes (or melts) at 273 K • water boils at 373 K Ø Ø <1/2 mv 2> = 3/2 k T The Kelvin is scale is the more useful scale for our course since it refers to Absolute Zero in a direct way. 10/26/2020 6

The Ideal Gas Law Laboratory experiments show that the pressure, volume, and temperature of any material may be related by an Equation of State (EOS). These variables are known as State Variables. All atmospheric gasses follow an equation of state known as the Ideal Gas Law (IGL) to a very high degree of accuracy. We assume the IGL to be exact in atmospheric science. The Ideal Gas Law may be written: p. V = m. RT where p = pressure V = volume m = mass T = temperature (absolute Kelvin; K = o. C + 273. 15) R = gas constant The gas constant R depends upon the particular gas under consideration. Since m/V = ρ (density of the gas), the IGL may be written: p = ρRT 10/26/2020 7

Ideal Gas Law (IGL) - continued We can also define α = 1/ρ, known as the specific volume, to write the IGL as: pα = RT Boyle’s Law: For fixed temperature, the pressure of a gas is inversely proportional to its volume, i. e. , P ~ 1/V. Additional forms of the Ideal Gas Law: A mole (gram-molecular weight) of any substance is the molecular weight M of the substance expressed in grams. For example, the molecular weight of water is 18. 015 gm, so 1 mole of water is 18. 015 gm of water. The number of moles (N) in a mass m (in grams) of a substance is given by: N = m/M The number of molecules in 1 mole of any substance is a universal constant called Avogadro’s number, NA. NA = 6. 022 x 1023 molecules per mole. 10/26/2020 8

Ideal Gas Law (IGL) – continued again The Ideal Gas Law for 1 mole of any gas can be written: p. V = R*T Where R* is the universal gas constant = 8. 3145 J K-1 mol-1. So for N moles of any gas, the IGL will be: p. V = NR*T The gas constant for 1 molecule of any gas is also a universal constant known as Boltzmann’s constant, k = 1. 38 x 10 -23 J K-1 molecule-1 So for a gas with n gas molecules per unit volume V, the IGL is then p = nk. T 10/26/2020 9

Ideal Gas Law - Summary Ideal Gas Law: P = nk. T = ρRT= RT/α PV = R*T/M P = pressure m = mass per gas particle n = number density of gas particles ρ = mn = mass density α = 1/ρ = specific volume V = volume of one mole of gas k = Boltzmann’s constant R = gas constant (gas specific) = R*/Μ M = molar mass R* = universal gas constant T = temperature 10/26/2020 10

Heat Capacity The Heat Capacity of a material is a measure of its ability to absorb and retain heat. More precisely, the Heat Capacity is the energy (d. Q) required to increase the temperature of a unit volume of any substance from T to T+d. T (in Kelvin) The Heat Capacity depends upon the nature of the material and its temperature. The Heat Capacity also depends upon exactly how the energy is added. If the heat is added to a gas at constant volume the heat capacity is lower than if the heat is added at constant pressure. The reason is that heat performs work if the volume changes. 10/26/2020 11

Heat Capacity - continued Heat capacity is related to the ability of a substance to store energy. Energy can be stored in a variety of ways. For a gas, the most obvious way to store energy is in random kinetic energy of the gas molecules. The 1/2 mv 2 is the kinetic energy of a molecule of mass m moving with a velocity v. There is ½ k. T of energy “per degree of freedom” of the molecule. For a molecule moving in 3 -dimensions, there are 3 degrees of freedom and thus the average kinetic energy is stored as 3/2 k. T. If there are other ways for a molecule to store energy, then the heat capacity will be higher. Thus the Heat Capacity depends upon the phase of the substance. 10/26/2020 12

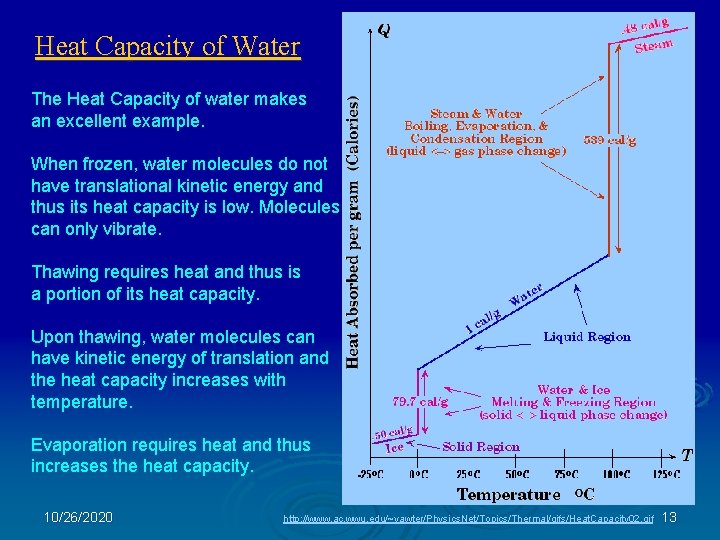
Heat Capacity of Water The Heat Capacity of water makes an excellent example. When frozen, water molecules do not have translational kinetic energy and thus its heat capacity is low. Molecules can only vibrate. Thawing requires heat and thus is a portion of its heat capacity. Upon thawing, water molecules can have kinetic energy of translation and the heat capacity increases with temperature. Evaporation requires heat and thus increases the heat capacity. 10/26/2020 http: //www. ac. wwu. edu/~vawter/Physics. Net/Topics/Thermal/gifs/Heat. Capacity 02. gif 13

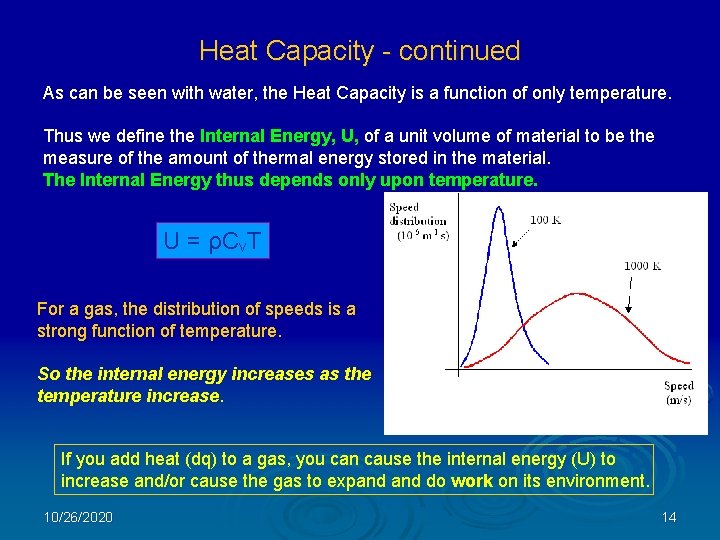
Heat Capacity - continued As can be seen with water, the Heat Capacity is a function of only temperature. Thus we define the Internal Energy, U, of a unit volume of material to be the measure of the amount of thermal energy stored in the material. The Internal Energy thus depends only upon temperature. U = ρCv. T For a gas, the distribution of speeds is a strong function of temperature. So the internal energy increases as the temperature increase. If you add heat (dq) to a gas, you can cause the internal energy (U) to increase and/or cause the gas to expand do work on its environment. 10/26/2020 14

Specific Heats Suppose a small quantity of heat dq is added to a unit mass of material and this causes the material to rise in temperature from T to T+d. T. Then is the specific heat of the material. If the volume of the material is kept constant, then the specific heat at constant volume Cv is defined as: However, if the volume of the material is kept constant, then dq = du (heat changes internal energy and does no work on the environment) and: For an ideal gas u depends only upon temperature (T), so Cv depends only upon T. 10/26/2020 15

Specific Heats - continued We can also define a specific heat at constant pressure Cp as: But when heat is added to a parcel of gas at constant pressure, some energy can be used in expanding the gas. So more heat must be added to a given mass of material at constant pressure to raise it to a given temperature than if the material was kept at constant volume. 10/26/2020 16

The 3 Laws of Thermodynamics Ø First Law: You can’t win. Ø Second Law: You can’t break even. Ø Third Law: You can’t get out of the game. 10/26/2020 17

The Three Laws of Thermodynamics 1) Conservation of Energy: Energy is neither created nor destroyed, it is merely converted from one form to another. 2) The Entropy of an isolated system increases when a system undergoes a spontaneous change. 3) The Entropy of all substances approaches zero as the temperature (in Kelvin) approaches zero. All substances have zero energy at absolute zero. 10/26/2020 18

The First Law of Thermodynamics Conservation of Energy: Energy is neither created nor destroyed, it is only changed from one form to another. What Forms of Energy: -- Gravitational Potential -- Kinetic Energy -- Chemical Energy -- Electromagnetic Energy -- Rest mass energy is Energy? For any system (e. g. a specific collection of matter), the change in energy of the system is equal to the energy transferred by work plus the energy transferred by heat. Heat is the transfer of energy to or from a system associated with a temperature difference. Work is the transfer of energy to a system by the application of a force. 10/26/2020 19

The first law of thermodynamics is the application of the conservation of energy principle to thermodynamic processes: http: //hyperphysics. phy-astr. gsu. edu/hbase/thermo/firlaw. html 10/26/2020 20

The First Law and Work http: //www. grc. nasa. gov/WWW/K-12/airplane/thermo 1. html 10/26/2020 21

10/26/2020 http: //www. fas. org/irp/imint/docs/rst/Sect 14/stability 2. jpg 22

Useful Forms of the First Law of Thermodynamics 10/26/2020 23

Second Law of Thermodynamics The Entropy of an isolated system increases when the system undergoes a spontaneous change. Entropy is the heat added (or subtracted), ΔQ, to a system divided by its temperature in Kelvin (T). It is a measure of the disorder of a system; a measure of the unavailability of a system’s energy to do work; a measure of the disorder of the molecules in a system; a measure of the number of possible states of a system. d. Q is the heat absorbed in an isothermal and reversible process. 10/26/2020 24

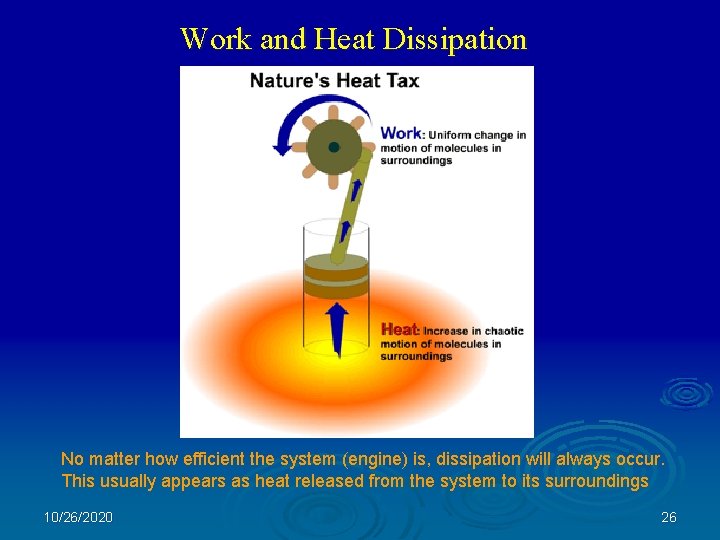
The Second Law of Thermodynamics states that it is impossible to completely convert heat energy into mechanical energy. Another way to put that is to say that the level of entropy (or tendency toward randomness) in a closed system is always either constant or increasing. Implications of the Second Law It is impossible for any process (e. g. , engine), working in a cycle, to completely convert surrounding heat to work. Ø Dissipation will always occur. Ø Entropy will always increase. Ø 10/26/2020 25

Work and Heat Dissipation No matter how efficient the system (engine) is, dissipation will always occur. This usually appears as heat released from the system to its surroundings 10/26/2020 26

Work and Heat http: //physics. uoregon. edu/~courses/dlivelyb/ph 161/heat_engine_schem. gif 10/26/2020 27

Work and Efficiency The Second Law of Thermodynamics states that it is impossible for any heat engine to be 100 % efficient: No process is possible which results in the extraction of an amount of heat from a reservoir and its conversion to an equal amount of mechanical work. 10/26/2020 28

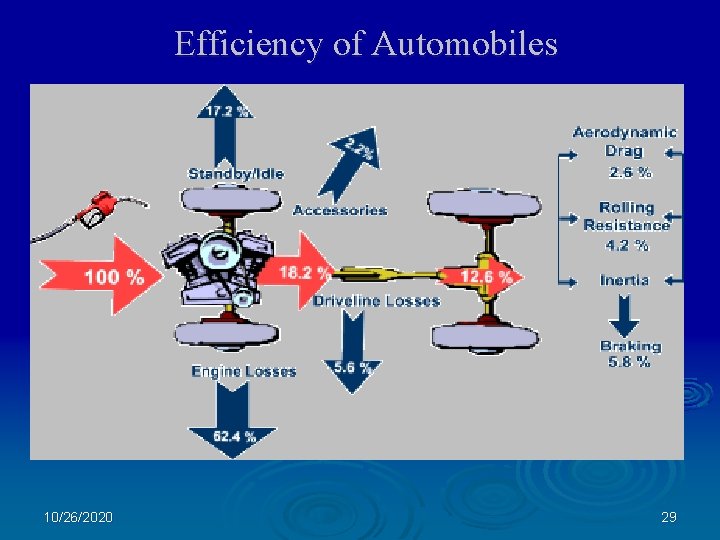
Efficiency of Automobiles 10/26/2020 29

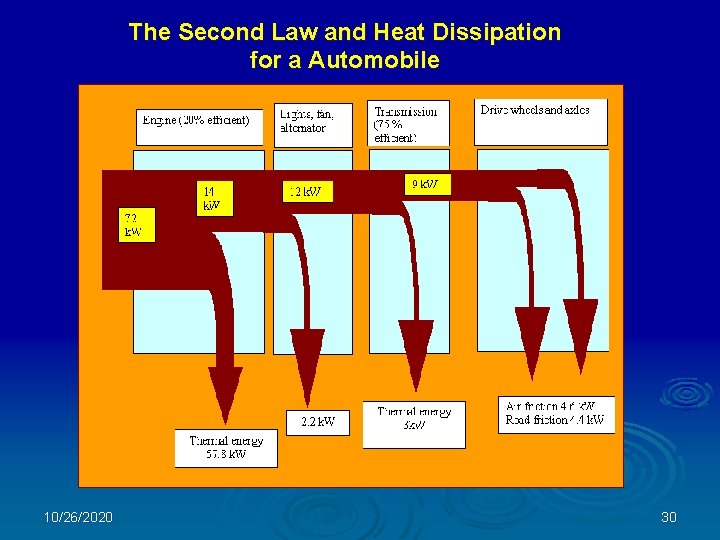
The Second Law and Heat Dissipation for a Automobile 10/26/2020 30

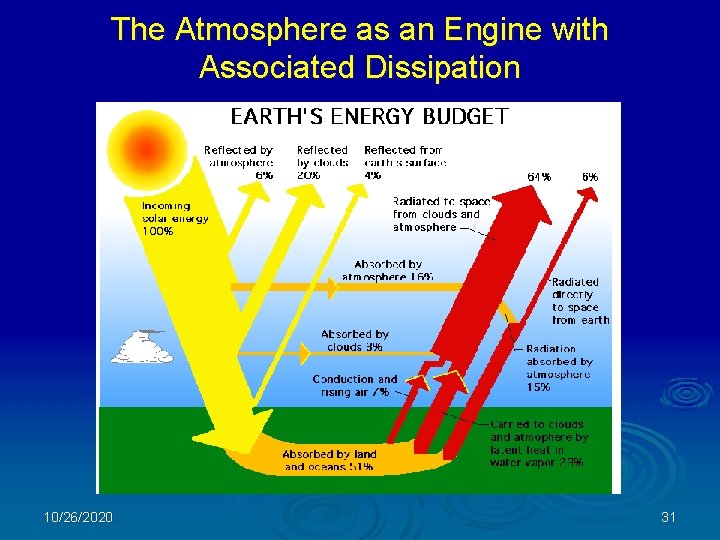
The Atmosphere as an Engine with Associated Dissipation 10/26/2020 31

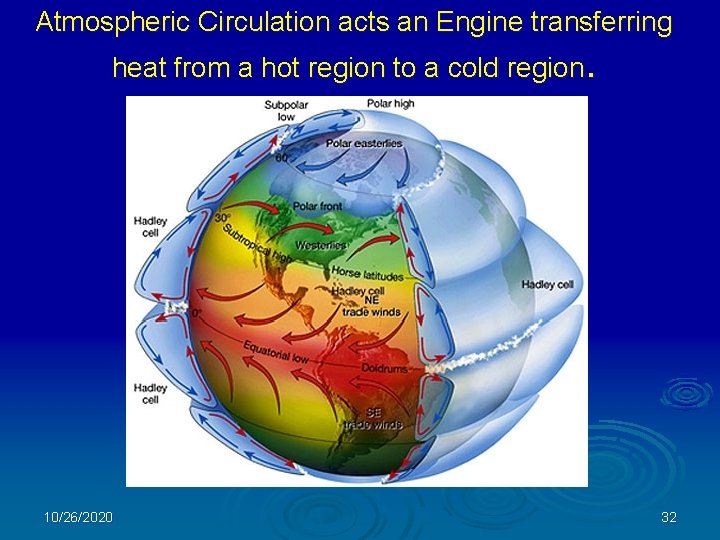
Atmospheric Circulation acts an Engine transferring heat from a hot region to a cold region. 10/26/2020 32

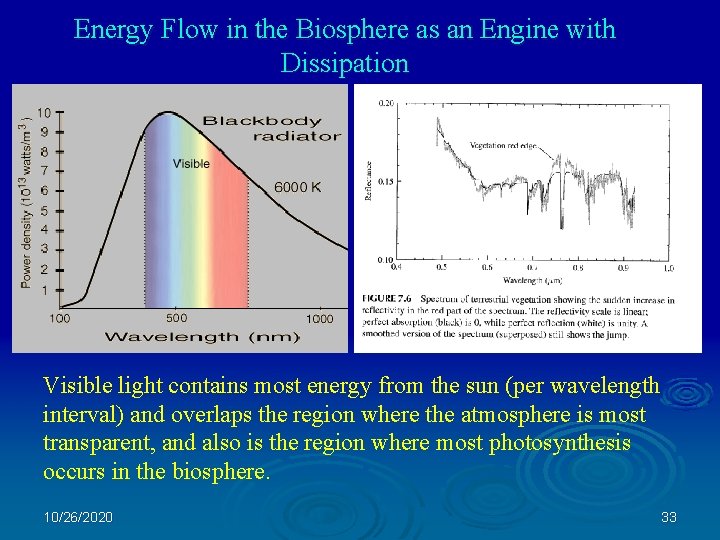
Energy Flow in the Biosphere as an Engine with Dissipation Visible light contains most energy from the sun (per wavelength interval) and overlaps the region where the atmosphere is most transparent, and also is the region where most photosynthesis occurs in the biosphere. 10/26/2020 33

Usable Energy http: //trc. ucdavis. edu/biosci 10 v/bis 10 v/week 2/2 webimages/figure-06 -03 b. jpg 10/26/2020 34

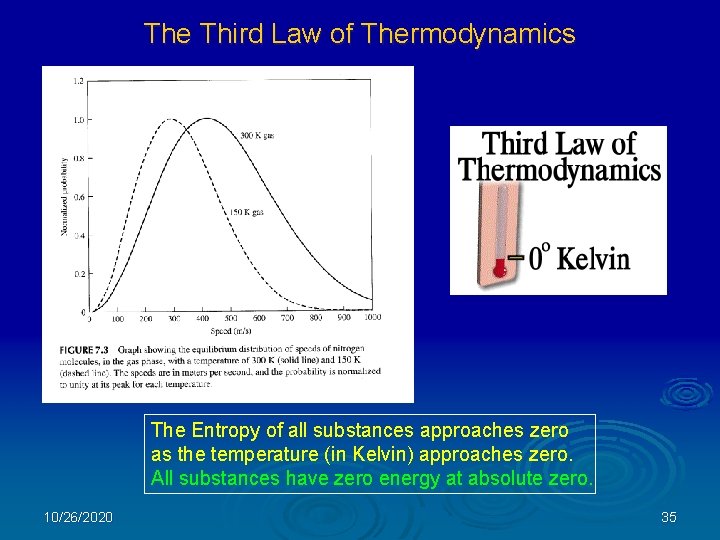
The Third Law of Thermodynamics The Entropy of all substances approaches zero as the temperature (in Kelvin) approaches zero. All substances have zero energy at absolute zero. 10/26/2020 35

The Use of Thermodynamic Diagrams A pair of variables: (P, V) or (P, T) or (V, T) or… denote a state of the system. A P-V diagram shows the possible states that the system can have. d. W = Pd. V = Force x Displacement 10/26/2020 36

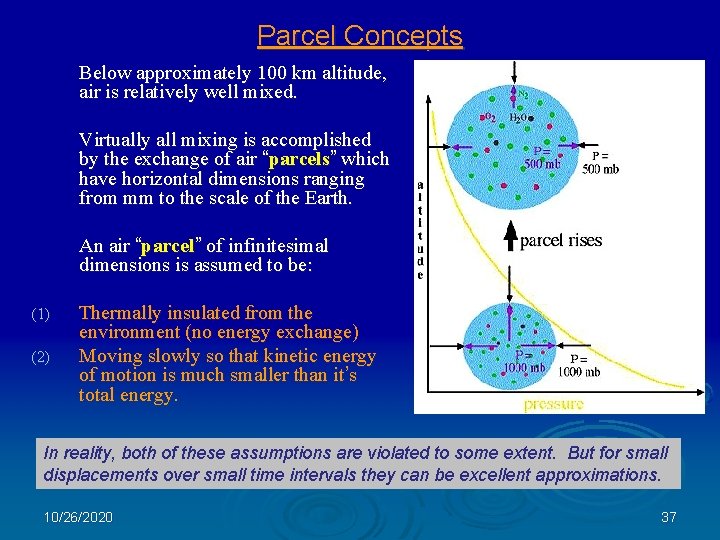
Parcel Concepts Below approximately 100 km altitude, air is relatively well mixed. Virtually all mixing is accomplished by the exchange of air “parcels” which have horizontal dimensions ranging from mm to the scale of the Earth. An air “parcel” of infinitesimal dimensions is assumed to be: (1) (2) Thermally insulated from the environment (no energy exchange) Moving slowly so that kinetic energy of motion is much smaller than it’s total energy. In reality, both of these assumptions are violated to some extent. But for small displacements over small time intervals they can be excellent approximations. 10/26/2020 37

Thermodynamic Descriptions of the Atmosphere During any atmospheric process, the state of a parcel of atmospheric gas (P, V, T, S, etc) will change. The Laws of Thermodynamics determine exactly how these changes can occur. Phase Diagrams describe these changes in the state variables describing the gas. 10/26/2020 38

Thermodynamic Descriptions of the Atmosphere During any atmospheric process, the state of a parcel of atmospheric gas (P, V, T, S, etc) will change. Any pair of variables can be used to describe the state of the system: (P, V) or (T, S) or (P, S), etc. 10/26/2020 39

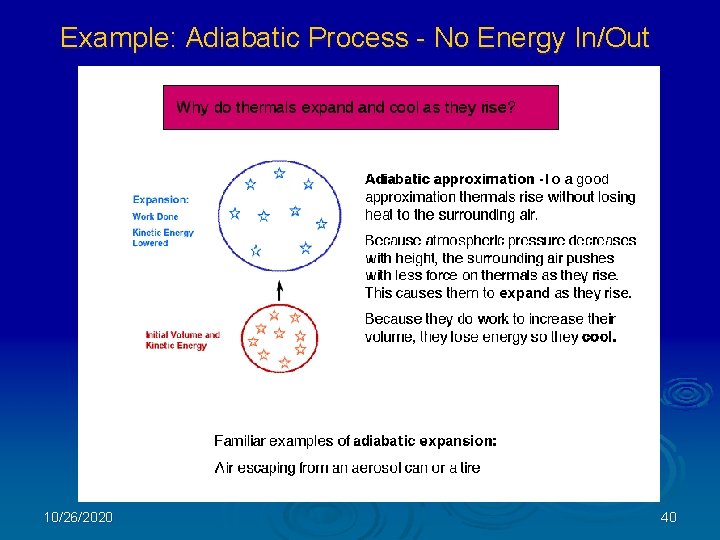
Example: Adiabatic Process - No Energy In/Out 10/26/2020 40

Parcel Concepts: Applications of the laws of thermodynamics to air parcels First Law of Thermodynamics: d. Q = d. U + Pd. V Internal Energy: d. U = C pd. T Second Law of Thermodynamics: d. S = d. Q/T Adiabatic means d. Q = 0. d. Q implies d. S = 0. Thus an adiabatic process is also an isentropic process. 10/26/2020 41

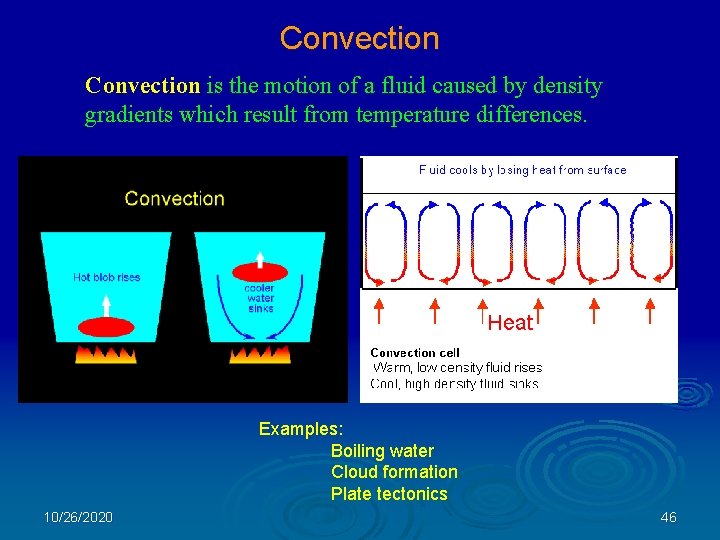
Energy Transport There are three primary ways that energy is transported in planetary atmospheres. (1) Conduction: is the transfer of energy by collisions between particles (generally atoms or molecules). Also known as diffusive transport of energy. (2) Convection: is the motion of a fluid caused by density gradients which are a result of temperature differences. (3) Radiation: is the transport of energy by photons. 10/26/2020 42

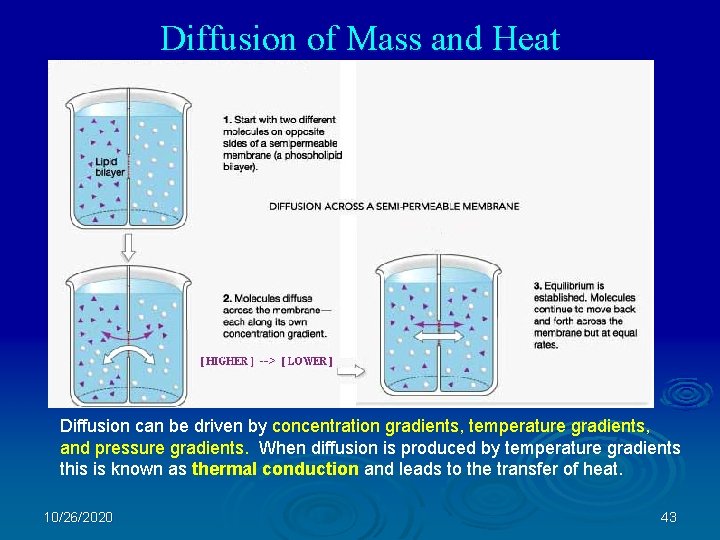
Diffusion of Mass and Heat Diffusion can be driven by concentration gradients, temperature gradients, and pressure gradients. When diffusion is produced by temperature gradients this is known as thermal conduction and leads to the transfer of heat. 10/26/2020 43

Thermal Conduction is the transfer of heat by collisions between particles Q = heat flux (erg cm-2 s-1) d. T/dz = temperature gradient in z direction κT = thermal conductivity is a measure of a material’s physical ability to conduct heat. Fick’s First Law of Diffusion The rate of change of energy per unit volume is given by: Fick’s Second Law of Diffusion 10/26/2020 44

Thermal Conduction is the transfer of heat by collisions between particles U = internal energy = ρCPT, where ρ = mass density CP = heat capacity at constant pressure (it can also occur at constant v) T = temperature Or Where κD = thermal diffusivity = κT/ρCP 10/26/2020 45

Convection is the motion of a fluid caused by density gradients which result from temperature differences. Examples: Boiling water Cloud formation Plate tectonics 10/26/2020 46

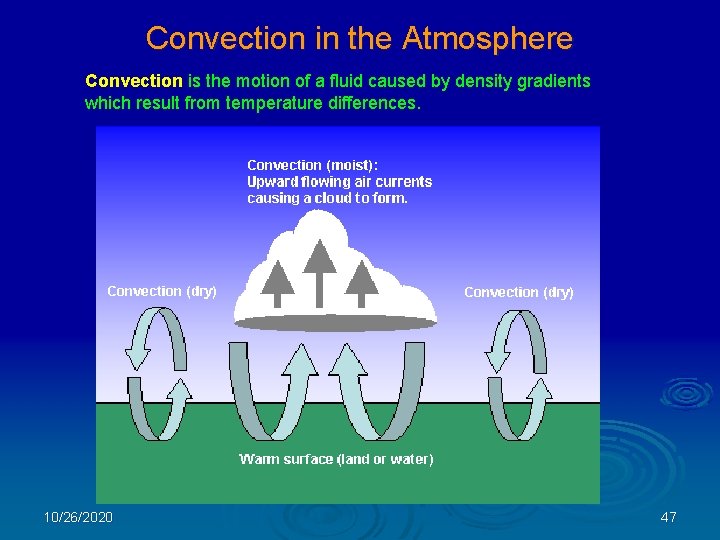
Convection in the Atmosphere Convection is the motion of a fluid caused by density gradients which result from temperature differences. 10/26/2020 47

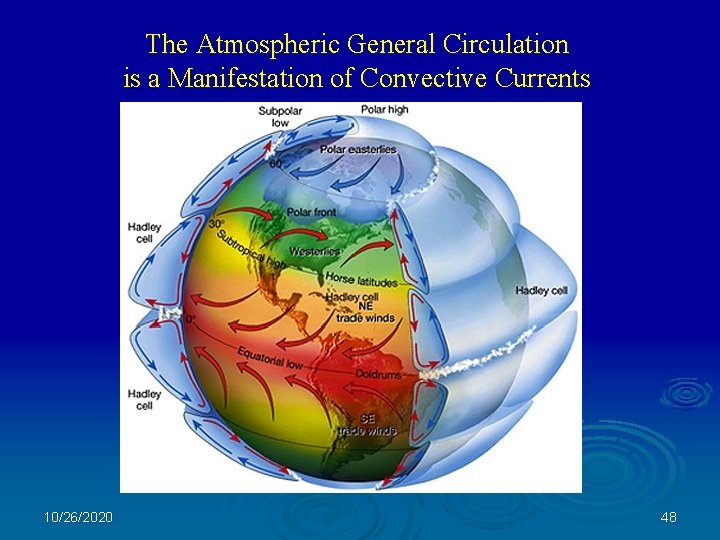
The Atmospheric General Circulation is a Manifestation of Convective Currents 10/26/2020 48

Quantifying Convective Energy Transport The Convective Energy Flux can be quantified analogous to thermal conduction flux, if thermal diffusion coefficient is replaced by an Eddy Diffusion Coefficient, Ke. First Law of Diffusion The rate of change of energy per unit volume is given by: Second Law of Diffusion Ke = Eddy Diffusion Coefficient The key problem in convection and mixing is the choice of Ke. It is usually determined by observations of tracer motions in the atmosphere. 10/26/2020 49

Energy Transport by Radiation c = 2. 998 x 108 ms-1 speed of electromagnetic radiation λ = wavelength (wavenumber = k = 1/λ) ν = frequency, such that: h = Planck’s Constant 10/26/2020 Energy: 50

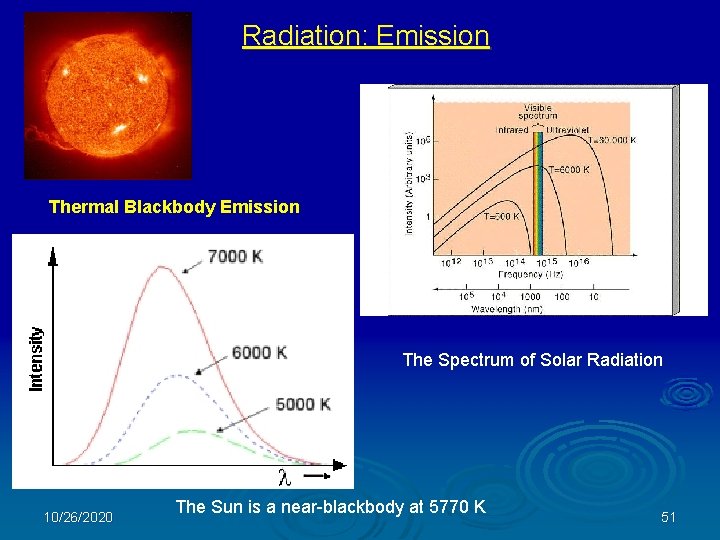
Radiation: Emission Thermal Blackbody Emission The Spectrum of Solar Radiation 10/26/2020 The Sun is a near-blackbody at 5770 K 51

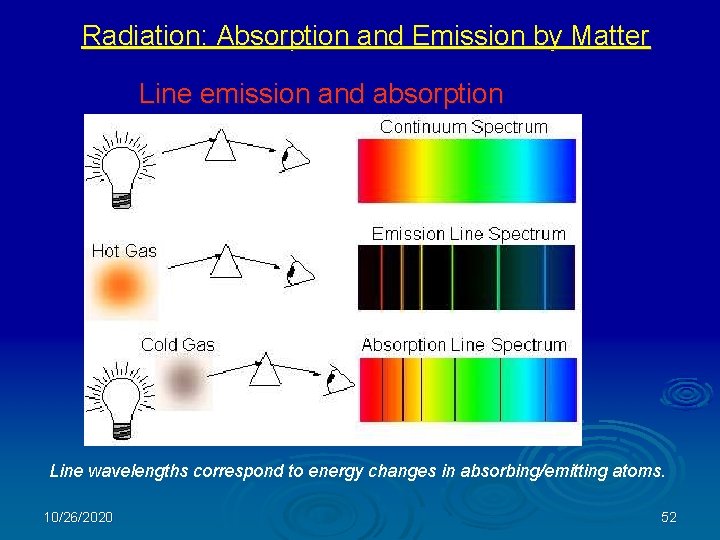
Radiation: Absorption and Emission by Matter Line emission and absorption Line wavelengths correspond to energy changes in absorbing/emitting atoms. 10/26/2020 52

Atomic Structure: Photon Absorption & Emission 10/26/2020 53

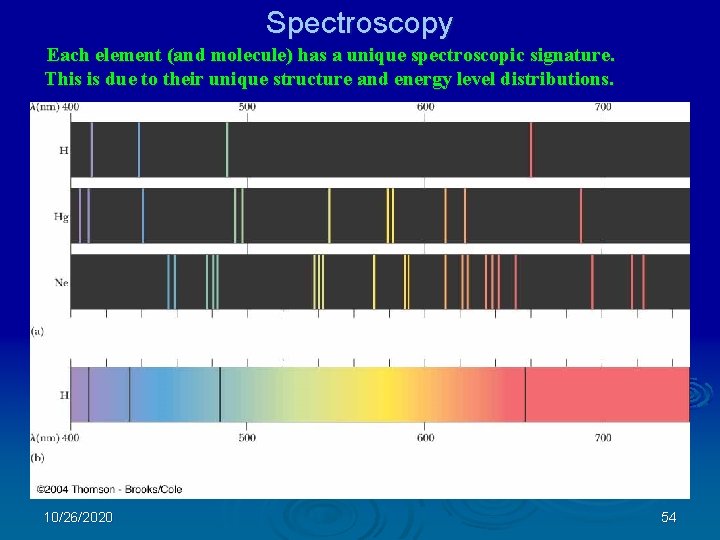
Spectroscopy Each element (and molecule) has a unique spectroscopic signature. This is due to their unique structure and energy level distributions. 10/26/2020 54

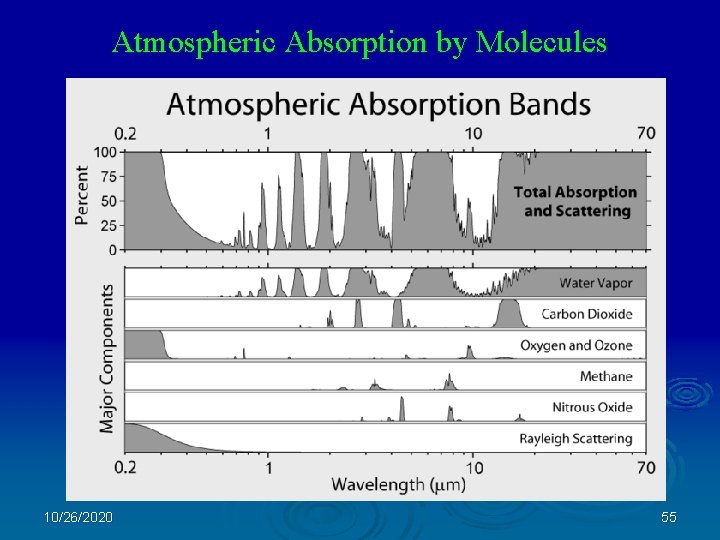
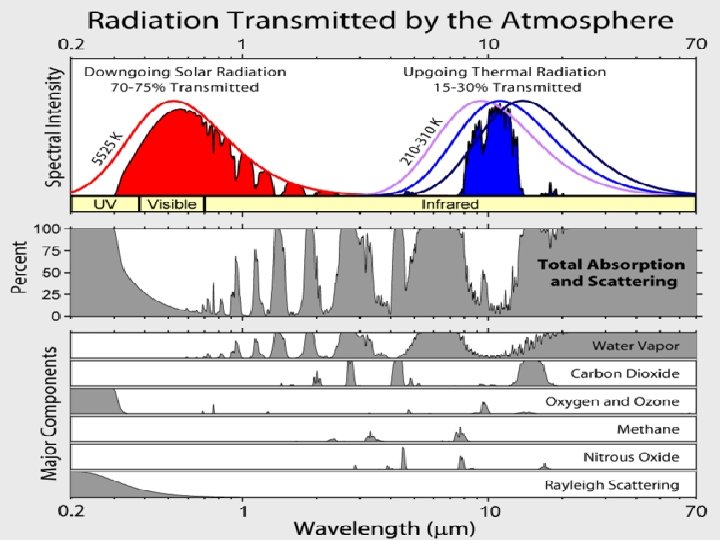
Atmospheric Absorption by Molecules 10/26/2020 55

10/26/2020 56

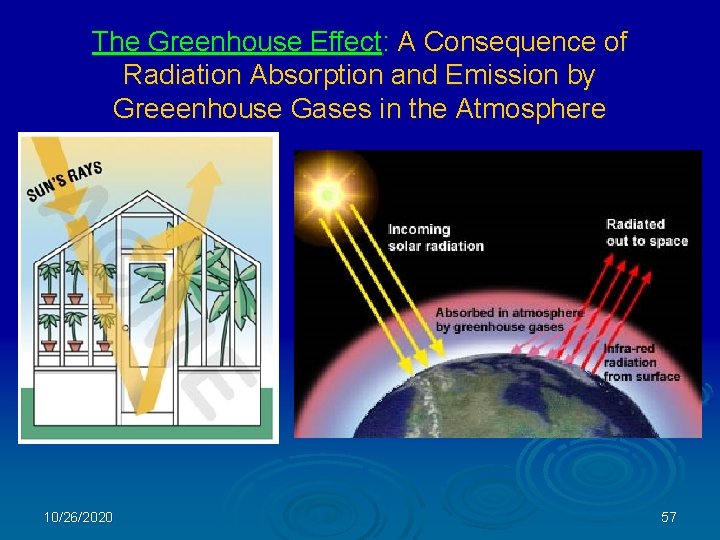
The Greenhouse Effect: A Consequence of Radiation Absorption and Emission by Greeenhouse Gases in the Atmosphere 10/26/2020 57

The Greenhouse Effect and Global Warming Sunlight brings energy into the climate system; most of it is absorbed by the oceans and land. THE GREENHOUSE EFFECT: Heat (infrared energy) radiates outward from the warmed surface of the Earth. Some of the infrared energy is absorbed by greenhouse gases in the atmosphere, which emits the energy in all directions. Some of this infrared energy further warms the Earth. GLOBAL WARMING: Increasing concentrations of CO 2 and other "greenhouse" gases trap more infrared energy in the atmosphere than occurs naturally. The additional heat further warms the atmosphere and Earth’s surface. 10/26/2020 58

Vertical Structure of the Earth’s Atmosphere: Illustration of Heat Transport Mechanisms Conduction: Solar extreme ultraviolet (EUV) photons absorbed in the upper atmosphere deposit energy which is conducted downwards. Radiation: Stratospheric ozone (O 3) absorb solar ultraviolet photons which cause local heating. Convection: The steep vertical temperature gradient produces unstable air parcels. 10/26/2020 59

Applications of Thermodynamics to Atmospheric Processes What is a Storm? Ø Parcel Concepts Ø Hydrostatic Equilibrium Ø Vertical Temperature Profile Ø Adiabatic Lapse Rate Ø Dry vs. Wet Atmosphere Ø Static Stability Ø The Second Law of Thermodynamics and the Atmosphere Ø 10/26/2020 60

What is a Storm? 1. Do all storms have the same cause? 2. Do all storms have the same ending? 3. Are there aspects that all storms have in common? http: //www. noaanews. noaa. gov/stories 2005/images/ivan 091504 -1515 zb. jpg 10/26/2020 61

Storm Definitions: Ø Ø Ø Ø behave violently, as if in state of a great anger take by force; "Storm the fort" rain, hail, or snow hard and be very windy, often with thunder or lightning; "If it storms, we'll need shelter" a violent weather condition with winds 64 -72 knots (11 on the Beaufort scale) and precipitation and thunder and lightning blow hard; "It was storming all night" a violent commotion or disturbance; "the storms that had characterized their relationship had died away"; "it was only a tempest in a teapot" attack by storm; attack suddenly a direct and violent assault on a stronghold 10/26/2020 62

What Causes a Storm? 10/26/2020 http: //systhread. net/pics/storm/jpegs-orig/10. jpg 63

How Long Can a Storm Last? 10/26/2020 Jupiter’s Giant Red Spot 64

Baby Red Spots? 10/26/2020 65

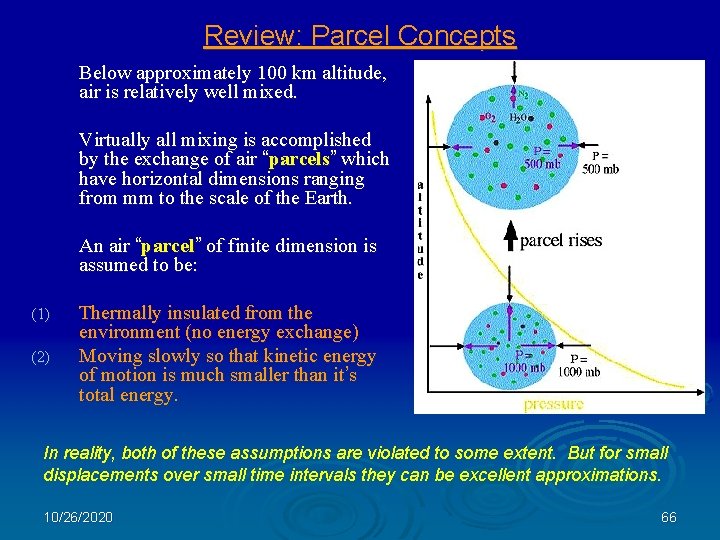
Review: Parcel Concepts Below approximately 100 km altitude, air is relatively well mixed. Virtually all mixing is accomplished by the exchange of air “parcels” which have horizontal dimensions ranging from mm to the scale of the Earth. An air “parcel” of finite dimension is assumed to be: (1) (2) Thermally insulated from the environment (no energy exchange) Moving slowly so that kinetic energy of motion is much smaller than it’s total energy. In reality, both of these assumptions are violated to some extent. But for small displacements over small time intervals they can be excellent approximations. 10/26/2020 66

How do you describe air Parcels? Ideal Gas Law - Summary Ideal Gas Law: P = nk. T = ρRT=RT/α PV = R*T/M P = pressure m = mass per gas particle n = number density of gas particles ρ = mn = mass density α = 1/ρ = specific volume V = volume of one mole of gas k = Boltzmann’s constant R = gas constant (gas specific) = R*/Μ M = molar mass R* = universal gas constant T = temperature 10/26/2020 67

Parcel Concepts: Applications of the laws of thermodynamics to air parcels Internal Energy (kinetic energy): Internal Energy (general): U = ρCp. T Internal Energy Change: d. U = Cpd. T; Work=Pd. V First Law of Thermodynamics: d. Q = d. U + Pd. V Second Law of Thermodynamics: d. S = d. Q/T Hydrostatic Equilibrium: d. P = -ρgdz Specific Heats (Constant P, V) Adiabatic means d. Q = 0. d. Q implies d. S = 0. Thus an adiabatic process is also an isentropic process. 10/26/2020 68

Hydrostatic Equilibrium Air pressure at any height in the atmosphere is due to the force per unit area exerted by the weight of all of the air lying above that height. The air is in hydrostatic balance if the net upward force on a thin slab of air is equal to the net downward force on the slab. Thus the change in pressure between the top and bottom of the thin slab is equal to the weight (d. M g = ρd. V g) of the slab per unit area, where d. V = d. Adz. Hydrostatic Balance: ρg d. Adz = P(z) d. A – P(z+dz) d. A P(z+dz) = P(z) + (d. P/dz) dz Thus d. P/dz = -ρg 10/26/2020 69

Hydrostatic Equilibrium Hydrostatic Balance: d. P = - ρgdz Ideal Gas Law: P = nk. T = (ρ/m) k. T = ρRT P = pressure m = mass per gas particle n = number density of gas particles ρ = mn = mass density k = Boltzmann constant R = gas constant T = temperature 10/26/2020 70

Hydrostatic Equilibrium This means that pressure falls off exponentially with altitude z. H = k. T/mg is the Atmospheric Scale Height, and is also the equivalent thickness of the atmosphere for constant temperature. Near the Earth’s surface, H ~ 7 -8 km. 10/26/2020 71

Atmospheric Scale Height where This means that pressure falls off exponentially with altitude z, with a e-folding “distance” in the vertical of H. For an isothermal atmosphere (T = constant), density would have the same functional form. H is also the equivalent “thickness” of the atmosphere. If the entire atmosphere was compressed to sea level pressure (Po), then the atmosphere would extend to a height of H. Near the Earth’s surface, H ~ 7 -8 km. H is also roughly the altitude to which an atom moving vertically can reach. This can be seen by equating an atom’s kinetic to gravitational potential energy: ½ mv 2 = 3/2 k. T = 3/2 mg. H 10/26/2020 72

Geopotential Height The Geopotential, Φ, at any point in the Earth’s atmosphere is defined as the work that must be done against the Earth’s gravitational field to raise a mass of 1 kg from sea level to that point. Units are J kg-1 or m 2 s-2. The force (in newtons) acting on 1 kg at height z above sea level is numerically equal to g. The work (in joules) done in raising 1 kg from z to z+dz is: From hydrostatic equilibrium (dp = -ρgdz) we get: The Geopotential at height z is then: 10/26/2020 73

We can also define a quantity called the Geopotential Height, Z, as: Where go is the globally averaged acceleration due to gravity at the Earth’s surface. Geopotential Height is used as the vertical coordinate in most atmospheric applications in which energy plays an important role (e. g. , large scale motions). In the lower atmosphere, there is only a small difference between the physical height z and the geopotential height Z. 10/26/2020 74

Thickness of Layer Between Pressure Levels In meteorological applications it is not convenient to deal with density, as it is difficult to measure. Pressure makes a more convenient vertical variable. Hydrostatic equilibrium: Geopotential: Integrate the geopotential between two pressure levels, p 1 and p 2. implies: From the definition of geopotential height: This is known as the thickness of the layer between two pressure layers. 10/26/2020 75

Scale Height for an Isothermal Atmosphere Thickness: If T = constant, OR if the mean temperature is used in this expression, then we get: Which can be integrated exactly: Or, by raising e to the power of each side: Scale Height: H = RT/go H ~ 7 -8 km in lower atmosphere 10/26/2020 76

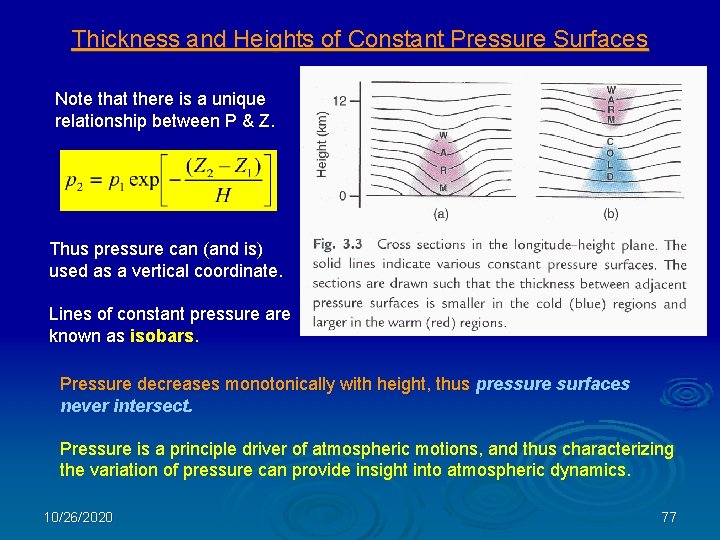
Thickness and Heights of Constant Pressure Surfaces Note that there is a unique relationship between P & Z. Thus pressure can (and is) used as a vertical coordinate. Lines of constant pressure are known as isobars. Pressure decreases monotonically with height, thus pressure surfaces never intersect. Pressure is a principle driver of atmospheric motions, and thus characterizing the variation of pressure can provide insight into atmospheric dynamics. 10/26/2020 77

First Law of Thermodynamics, Once Again d. Q = d. U + Pd. V Heat Flow (in/out) = change in internal energy + work done by parcel Using the specific heat relationship we have d. U = Cv d. T So we can write: d. Q = Cv d. T + Pd. V as equivalent statement of the First Law of Thermodynamics. 10/26/2020 78

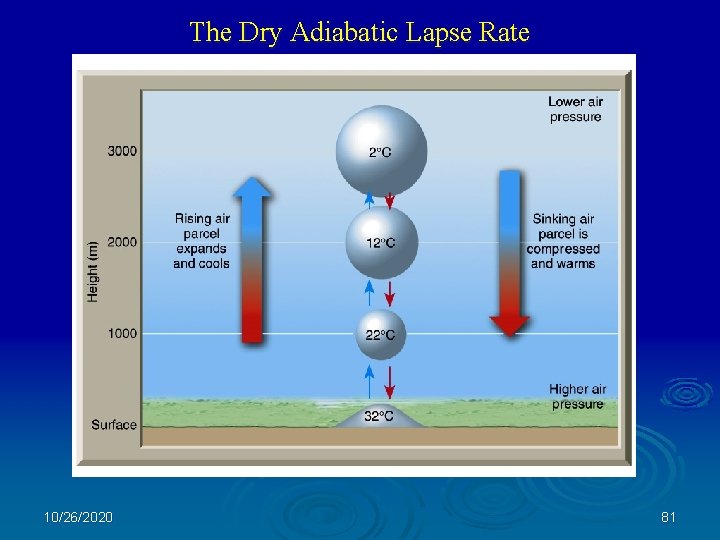
Derivation of the Dry Adiabatic Lapse Rate (DALR) Hydrostatic Equilibrium: d. P = -ρg dz, or Vd. P = -g dz (where V = specific volume = 1/ρ) Ideal Gas Law: P = ρRT = RT/ V First Law of Thermodynamics: d. Q = Cvd. T + P d. V Rewrite IGL PV = RT Differentiate the IGL P d. V + V d. P = Rd. T = (Cp-Cv) d. T (For an ideal gas Cp – Cv = R) Combine FLT & IGL d. Q = Cv d. T + (Cp-Cv) d. T – V d. P d. Q = C pd. T – V d. P But for an adiabatic process (no energy flow into or out of the parcel) d. Q = 0 So Cpd. T = V d. P = -g dz d. T/dz = -g/Cp DALR Note that the DALR doesn’t say anything about the actual value of T, but it provides a very strong constraint on how T varies with altitude. 10/26/2020 79

Adiabatic Processes for Parcels If we slowly move a parcel of dry air vertically, such that there is no energy flow with its environment (d. Q=0), then its temperature will change with altitude following the Dry Adiabatic Lapse Rate (DALR). 10/26/2020 80

The Dry Adiabatic Lapse Rate 10/26/2020 81

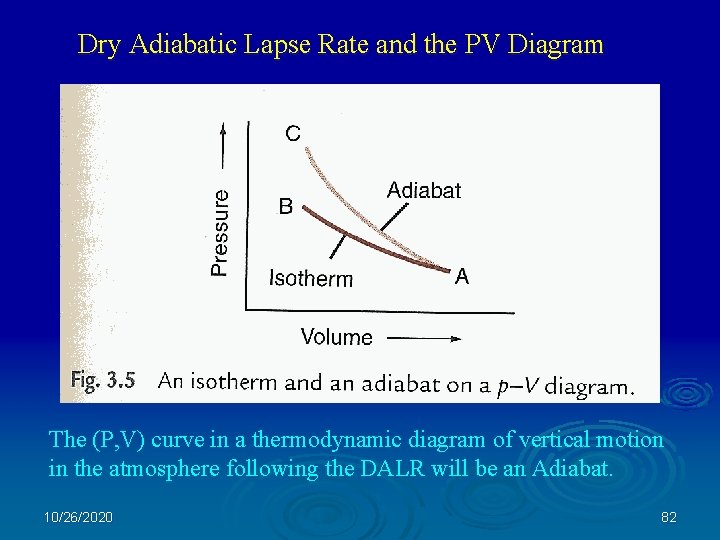
Dry Adiabatic Lapse Rate and the PV Diagram The (P, V) curve in a thermodynamic diagram of vertical motion in the atmosphere following the DALR will be an Adiabat. 10/26/2020 82

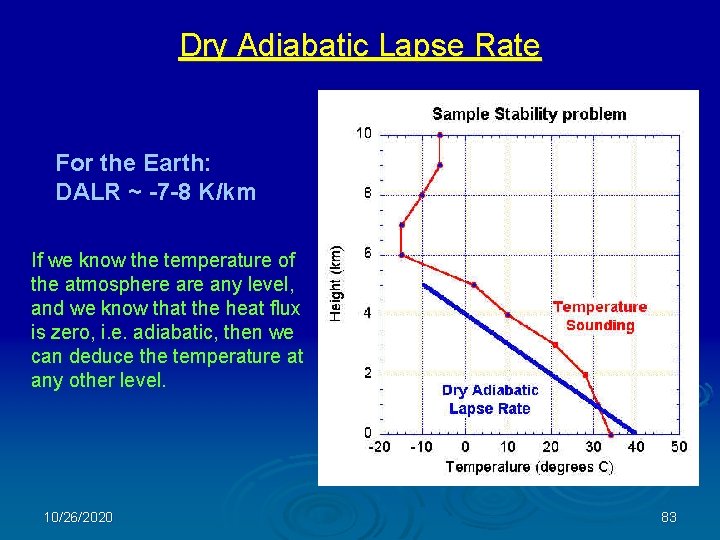
Dry Adiabatic Lapse Rate For the Earth: DALR ~ -7 -8 K/km If we know the temperature of the atmosphere any level, and we know that the heat flux is zero, i. e. adiabatic, then we can deduce the temperature at any other level. 10/26/2020 83

Entropy and Potential Temperature First Law of Thermodynamics: d. Q = d. U + Pd. V = d. U - Vd. P Internal Energy: d. U = Cp d. T Second Law of Thermodynamics: d. S = d. Q/T S = Entropy of the system 10/26/2020 84

Entropy and Potential Temperature FLT SLT Integration Rewrite: 10/26/2020 Where κ =R/Cp (approximately 2/7 for a diatomic gas) So is the constant of integration. 85

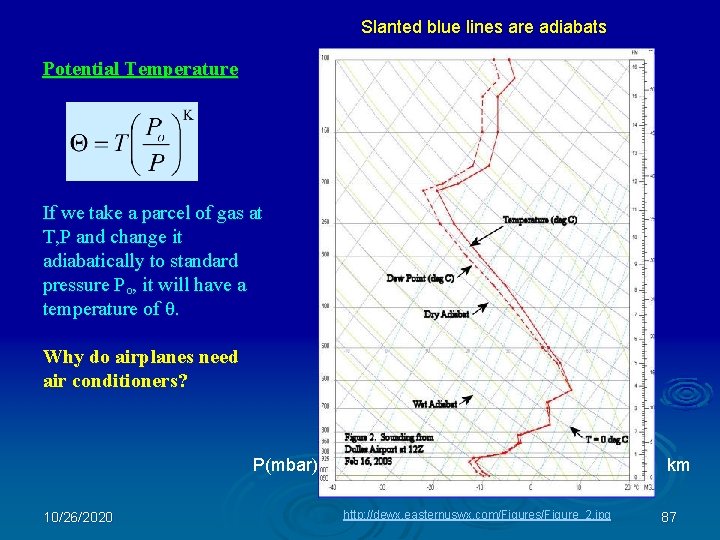
Adiabatic Processes: d. Q = 0 Constant Entropy Processes: d. S = 0 From the Second Law of Thermodynamics d. S = d. Q/T, an adiabatic process is thus an isentropic process. d. S=0 Integrate: Potential Temperature 10/26/2020 86

Slanted blue lines are adiabats Potential Temperature If we take a parcel of gas at T, P and change it adiabatically to standard pressure Po, it will have a temperature of θ. Why do airplanes need air conditioners? P(mbar) 10/26/2020 km http: //dewx. easternuswx. com/Figures/Figure_2. jpg 87

Parcel Concepts: Key Ideas Internal Energy (kinetic energy): Internal Energy (general): U = ρ Cp. T Internal Energy Change: d. U = Cpd. T; Work=Pd. V First Law of Thermodynamics: d. Q = d. U + Pd. V Second Law of Thermodynamics: d. S = d. Q/T Hydrostatic Equilibrium: d. P = -ρ gdz Specific Heats (at constant P) Specific Heats (at constant V) 10/26/2020 88