Performance Evaluation of Parallel Processing XianHe Sun Illinois

Performance Evaluation of Parallel Processing Xian-He Sun Illinois Institute of Technology Sun@iit. edu X. Sun (IIT) CS 546 1

Outline • Performance metrics – Speedup – Efficiency – Scalability • Examples • Reading: Kumar – ch 5 X. Sun (IIT) CS 546 2

Performance Evaluation (Improving performance is the goal) • Performance Measurement – Metric, Parameter • Performance Prediction – Model, Application-Resource • Performance Diagnose/Optimization – Post-execution, Algorithm improvement, Architecture improvement, State-of-the-art, Scheduling, Resource management/Scheduling X. Sun (IIT) CS 546 3

Parallel Performance Metrics (Run-time is the dominant metric) • Run-Time (Execution Time) • Speed: mflops, mips, cpi • Efficiency: throughput • Speedup • Parallel Efficiency • Scalability: The ability to maintain performance gain when system and problem size increase • Others: portability, programming ability, etc X. Sun (IIT) CS 546 4

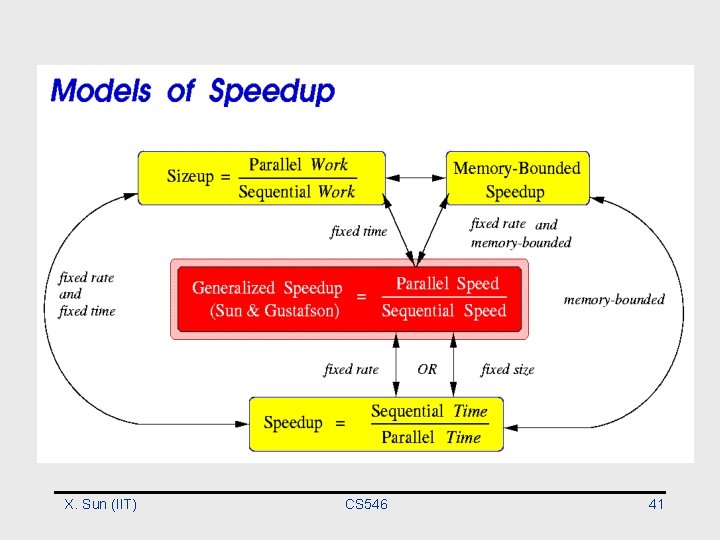
Performance Evaluation of Parallel Processing Models of Speedup • Speedup • Scaled Speedup – Parallel processing gain over sequential processing, where problem size scales up with computing power (having sufficient workload/parallelism) X. Sun (IIT) CS 546 5

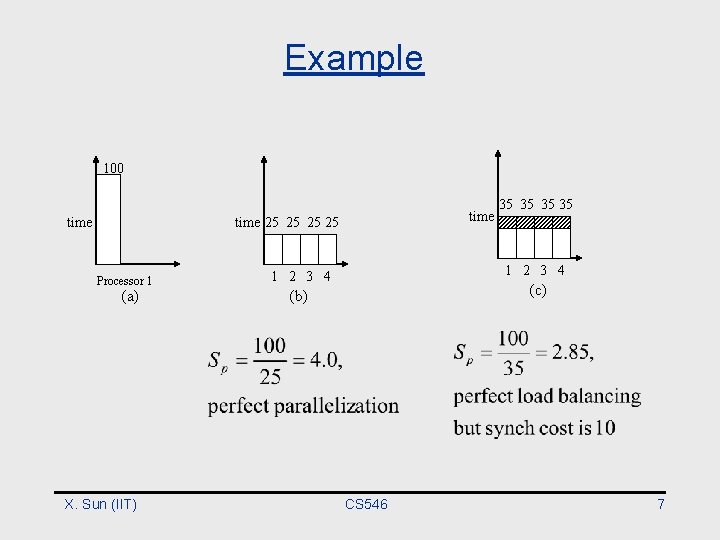
Speedup • Ts =time for the best serial algorithm • Tp=time for parallel algorithm using p processors X. Sun (IIT) CS 546 6

Example 100 time 25 25 Processor 1 (a) X. Sun (IIT) 35 35 1 2 3 4 (c) (b) CS 546 7

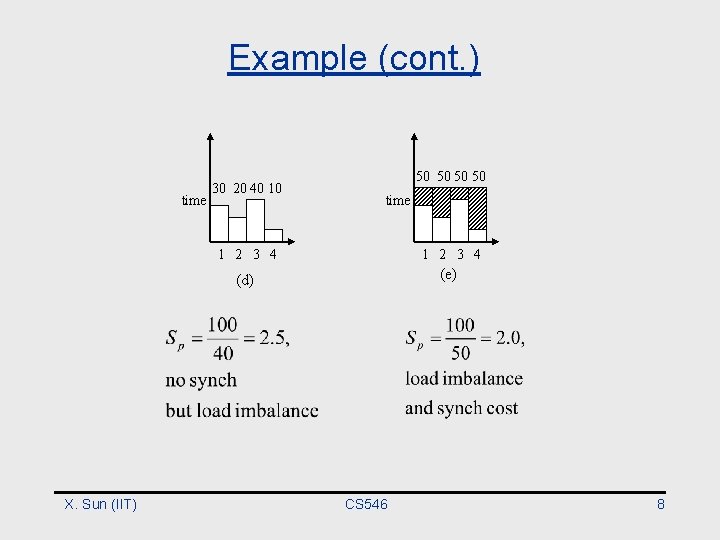
Example (cont. ) time X. Sun (IIT) 30 20 40 10 50 50 time 1 2 3 4 (d) (e) CS 546 8

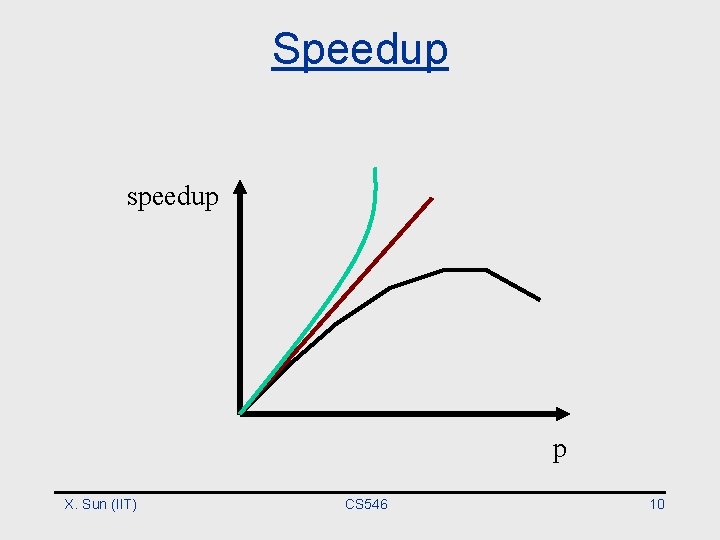
What Is “Good” Speedup? • Linear speedup: • Superlinear speedup • Sub-linear speedup: X. Sun (IIT) CS 546 9

Speedup speedup p X. Sun (IIT) CS 546 10

Sources of Parallel Overheads • • Interprocessor communication Load imbalance Synchronization Extra computation X. Sun (IIT) CS 546 11

Degradations of Parallel Processing Unbalanced Workload Communication Delay Overhead Increases with the Ensemble Size X. Sun (IIT) CS 546 12

Degradations of Distributed Computing Unbalanced Computing Power and Workload Shared Computing and Communication Resource Uncertainty, Heterogeneity, and Overhead Increases with the Ensemble Size X. Sun (IIT) CS 546 13

Causes of Superlinear Speedup • • • Cache size increased Overhead reduced Latency hidden Randomized algorithms Mathematical inefficiency of the serial algorithm Higher memory access cost in sequential processing • X. H. Sun, and J. Zhu, "Performance Considerations of Shared Virtual Memory Machines, " IEEE Trans. on Parallel and Distributed Systems, Nov. 1995 X. Sun (IIT) CS 546 14

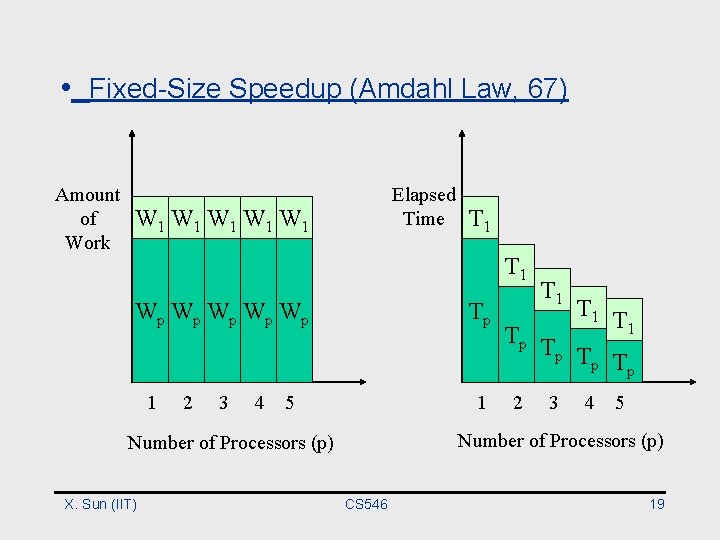
• Fixed-Size Speedup (Amdahl’s law) – Emphasis on turnaround time – Problem size, W, is fixed X. Sun (IIT) CS 546 15

Amdahl’s Law • The performance improvement that can be gained by a parallel implementation is limited by the fraction of time parallelism can actually be used in an application • Let = fraction of program (algorithm) that is serial and cannot be parallelized. For instance: – Loop initialization – Reading/writing to a single disk – Procedure call overhead • Parallel run time is given by X. Sun (IIT) CS 546 16

Amdahl’s Law • Amdahl’s law gives a limit on speedup in terms of X. Sun (IIT) CS 546 17

Enhanced Amdahl’s Law • To include overhead • The overhead includes parallelism and interaction overheads Amdahl’s law: argument against massively parallel systems X. Sun (IIT) CS 546 18

• Fixed-Size Speedup (Amdahl Law, 67) Amount of Work Elapsed Time W 1 W 1 W 1 T 1 Wp Wp Wp 1 2 3 4 Tp 5 1 T 1 Tp T p Tp 2 3 4 5 Number of Processors (p) X. Sun (IIT) T 1 CS 546 19

Amdahl’s Law • The speedup that is achievable on p processors is: • If we assume that the serial fraction is fixed, then the speedup for infinite processors is limited by 1/ • For example, if =10%, then the maximum speedup is 10, even if we use an infinite number of processors X. Sun (IIT) CS 546 20

Comments on Amdahl’s Law • The Amdahl’s fraction in practice depends on the problem size n and the number of processors p • An effective parallel algorithm has: • For such a case, even if one fixes p, we can get linear speedups by choosing a suitable large problem size • Scalable speedup • Practically, the problem size that we can run for a particular problem is limited by the time and memory of the parallel computer X. Sun (IIT) CS 546 21

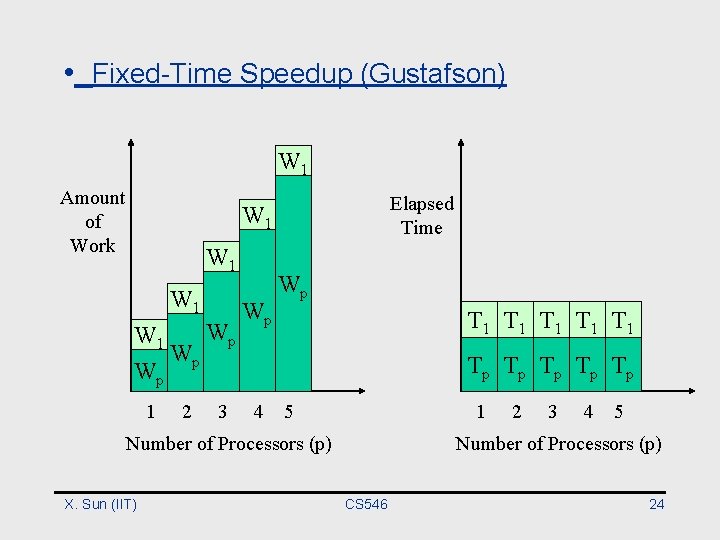
• Fixed-Time Speedup (Gustafson, 88) ° Emphasis on work finished in a fixed time ° Problem size is scaled from W to W' ° W': Work finished within the fixed time with parallel processing X. Sun (IIT) CS 546 22

Gustafson’s Law (Without Overhead) p (1 -a)p a X. Sun (IIT) 1 -a CS 546 time 23

• Fixed-Time Speedup (Gustafson) W 1 Amount of Work Elapsed Time W 1 W 1 Wp Wp 1 2 Wp Wp Wp T 1 T 1 T 1 Tp Tp Tp 3 4 5 1 Number of Processors (p) X. Sun (IIT) 2 3 4 5 Number of Processors (p) CS 546 24

Converting ’s between Amdahl’s and Gustafon’s laws Based on this observation, Amdahl’s and Gustafon’s laws are identical. X. Sun (IIT) CS 546 25

Memory Constrained Scaling: Sun and Ni’s Law • Scale the largest possible solution limited by the memory space. Or, fix memory usage per processor – (ex) N-body problem • Problem size is scaled from W to W* • W* is the work executed under memory limitation of a parallel computer • For simple profile, and G(n) is the increase of parallel workload as the memory capacity increases p times. X. Sun (IIT) CS 546 27

Sun & Ni’s Law p (1 -a)G(p) a X. Sun (IIT) 1 -a CS 546 time 28

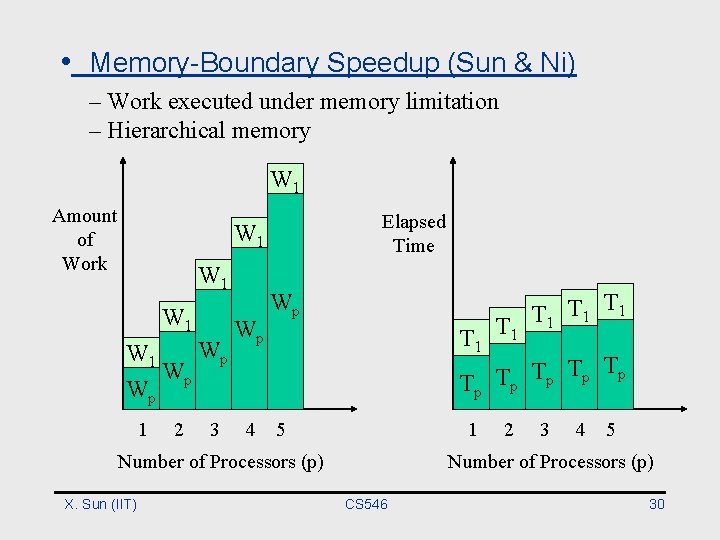
• Memory-Bounded Speedup (Sun & Ni, 90) ° Emphasis on work finished under current physical limitation ° Problem size is scaled from W to W* ° W*: Work executed under memory limitation with parallel processing • X. H. Sun, and L. Ni , "Scalable Problems and Memory-Bounded Speedup, " Journal of Parallel and Distributed Computing, Vol. 19, pp. 27 -37, Sept. 1993 (SC 90). X. Sun (IIT) CS 546 29

• Memory-Boundary Speedup (Sun & Ni) – Work executed under memory limitation – Hierarchical memory W 1 Amount of Work Elapsed Time W 1 W 1 Wp Wp 1 2 3 Wp T 1 T T 1 1 T 1 Tp Tp T T p Wp p 4 5 1 Number of Processors (p) X. Sun (IIT) 2 3 4 5 Number of Processors (p) CS 546 30

Characteristics • Connection to other scaling models – G(p) = 1, problem constrained scaling – G(p) = p, time constrained scaling • With overhead • G(p) > p, can lead to large increase in execution time – (ex) 10 K x 10 K matrix factorization: 800 MB, 1 hr in uniprocessor with 1024 processors, 320 K x 320 K matrix, 32 hrs X. Sun (IIT) CS 546 31

Why Scalable Computing – Scalable More accurate solution Sufficient parallelism Maintain efficiency – Efficient in parallel computing Load balance Communication – Mathematically effective Adaptive Accuracy X. Sun (IIT) CS 546 32

• Memory-Bounded Speedup ° Natural for domain decomposition based computing ° Show the potential of parallel processing (In gerneal, computing requirement increases faster with problem size than that of communication) ° Impacts extend to architecture design: trade-off of memory size and computing speed X. Sun (IIT) CS 546 33

Why Scalable Computing (2) Small Work • Appropriate for small machine – Parallelism overheads begin to dominate benefits for larger machines • Load imbalance • Communication to computation ratio – May even achieve slowdowns – Does not reflect real usage, and inappropriate for large machine • Can exaggerate benefits of improvements X. Sun (IIT) CS 546 34

Why Scalable Computing (3) Large Work • Appropriate for big machine – Difficult to measure improvement – May not fit for small machine • Can’t run • Thrashing to disk • Working set doesn’t fit in cache – Fits at some p, leading to superlinear speedup X. Sun (IIT) CS 546 35

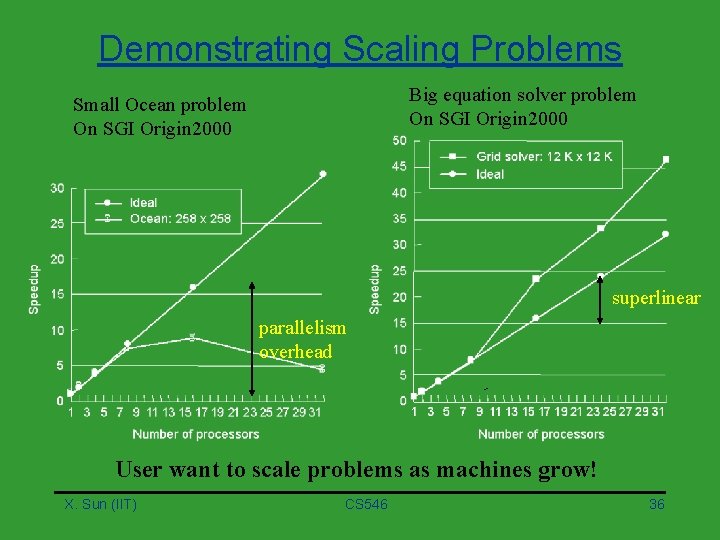
Demonstrating Scaling Problems Big equation solver problem On SGI Origin 2000 Small Ocean problem On SGI Origin 2000 superlinear parallelism overhead User want to scale problems as machines grow! X. Sun (IIT) CS 546 36

How to Scale • Scaling a machine – Make a machine more powerful – Machine size • <processor, memory, communication, I/O> – Scaling a machine in parallel processing • Add more identical nodes • Problem size – Input configuration – data set size : the amount of storage required to run it on a single processor – memory usage : the amount of memory used by the program X. Sun (IIT) CS 546 37

Two Key Issues in Problem Scaling • Under what constraints should the problem be scaled? – Some properties must be fixed as the machine scales • How should the problem be scaled? – Which parameters? – How? X. Sun (IIT) CS 546 38

Constraints To Scale • Two types of constraints – Problem-oriented • Ex) Time – Resource-oriented • Ex) Memory • Work to scale – Metric-oriented • Floating point operation, instructions – User-oriented • Easy to change but may difficult to compare • Ex) particles, rows, transactions • Difficult cross comparison X. Sun (IIT) CS 546 39

Rethinking of Speedup • Speedup • Why it is called speedup but compare time • Could we compare speed directly? • Generalized speedup • X. H. Sun, and J. Gustafson, "Toward A Better Parallel Performance Metric, " Parallel Computing, Vol. 17, pp. 1093 -1109, Dec. 1991. X. Sun (IIT) CS 546 40

X. Sun (IIT) CS 546 41

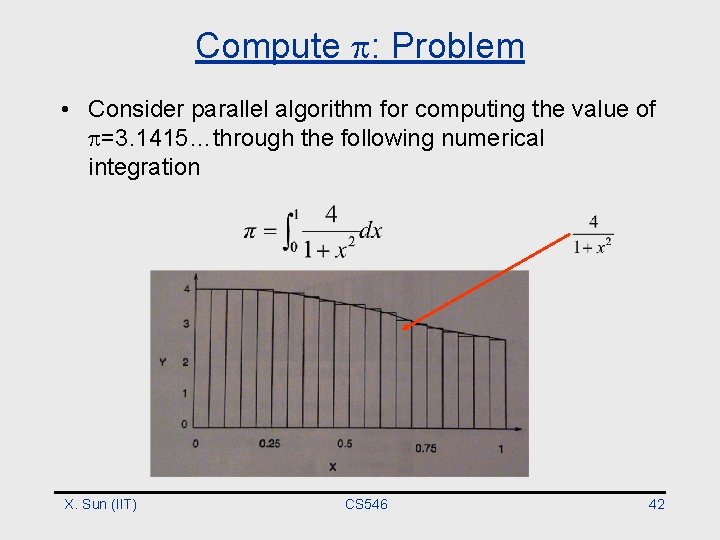
Compute : Problem • Consider parallel algorithm for computing the value of =3. 1415…through the following numerical integration X. Sun (IIT) CS 546 42

Compute : Sequential Algorithm computepi() { h=1. 0/n; sum =0. 0; for (i=0; i<n; i++) { x=h*(i+0. 5); sum=sum+4. 0/(1+x*x); } pi=h*sum; } X. Sun (IIT) CS 546 43

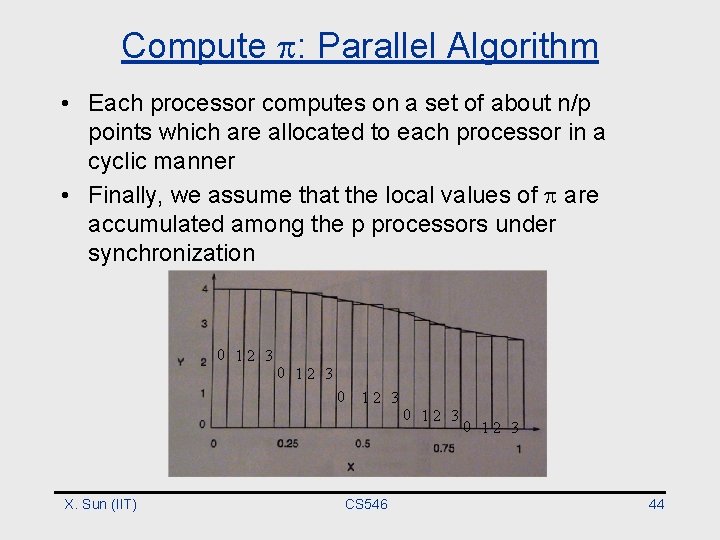
Compute : Parallel Algorithm • Each processor computes on a set of about n/p points which are allocated to each processor in a cyclic manner • Finally, we assume that the local values of are accumulated among the p processors under synchronization 12 3 0 CS 546 0 0 X. Sun (IIT) 12 3 0 0 12 3 44

Compute : Parallel Algorithm computepi() { id=my_proc_id(); nprocs=number_of_procs(): h=1. 0/n; sum=0. 0; for(i=id; i<n; i=i+nprocs) { x=h*(i+0. 5); sum=sum+4. 0/(1+x*x); } localpi=sum*h; use_tree_based_combining_for_critical_section(); pi=pi+localpi; end_critical_section(); } X. Sun (IIT) CS 546 45

Compute : Analysis • Assume that the computation of is performed over n points • The sequential algorithm performs 6 operations (two multiplications, one division, three additions) per points on the xaxis. Hence, for n points, the number of operations executed in the sequential algorithm is: 3 additions for (i=0; i<n; i++) { x=h*(i+0. 5); sum=sum+4. 0/(1+x*x); } 1 division 2 multiplications X. Sun (IIT) CS 546 46

Compute : Analysis • The parallel algorithm uses p processors with static interleaved scheduling. Each processor computes on a set of m points which are allocated to each process in a cyclic manner • The expression for m is given by if p does not exactly divide n. The runtime for the parallel algorithm for the parallel computation of the local values of is: X. Sun (IIT) CS 546 47

Compute : Analysis • The accumulation of the local values of using a tree -based combining can be optimally performed in log 2(p) steps • The total runtime for the parallel algorithm for the computation of including the parallel computation and the combining is: • The speedup of the parallel algorithm is: X. Sun (IIT) CS 546 48

Compute : Analysis • The Amdahl’s fraction for this parallel algorithm can be determined by rewriting the previous equation as: • Hence, the Amdahl’s fraction (n, p) is: • The parallel algorithm is effective because: X. Sun (IIT) CS 546 49

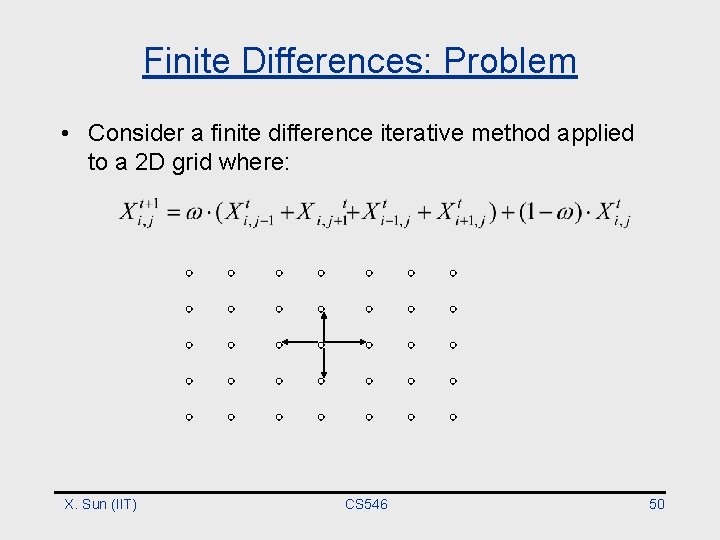
Finite Differences: Problem • Consider a finite difference iterative method applied to a 2 D grid where: X. Sun (IIT) CS 546 50

Finite Differences: Serial Algorithm finitediff() { for (t=0; t<T; t++) { for (i=0; i<n; i++) { for (j=0; j<n; j++) { x[i, j]=w_1*(x[i, j-1]+x[i, j+1]+x[i-1, j]+x[i+1, j]+w_2*x[i, j]; } } X. Sun (IIT) CS 546 51

Finite Differences: Parallel Algorithm • Each processor computes on a sub-grid of points • Synch between processors after every iteration ensures correct values being used for subsequent iterations X. Sun (IIT) CS 546 52

Finite Differences: Parallel Algorithm finitediff() { row_id=my_processor_row_id(); col_id=my_processor_col_id(); p=numbre_of_processors(); sp=sqrt(p); rows=cols=ceil(n/sp); row_start=row_id*rows; col_start=col_id*cols; for (t=0; t<T; t++) { for (i=row_start; i<min(row_start+rows, n); i++) { for (j=col_start; j<min(col_start+cols, n); j++) { x[i, j]=w_1*(x[i, j-1]+x[i, j+1]+x[i-1, j]+x[i+1, j]+w_2*x[i, j]; } barrier(); } } }X. Sun (IIT) CS 546 53

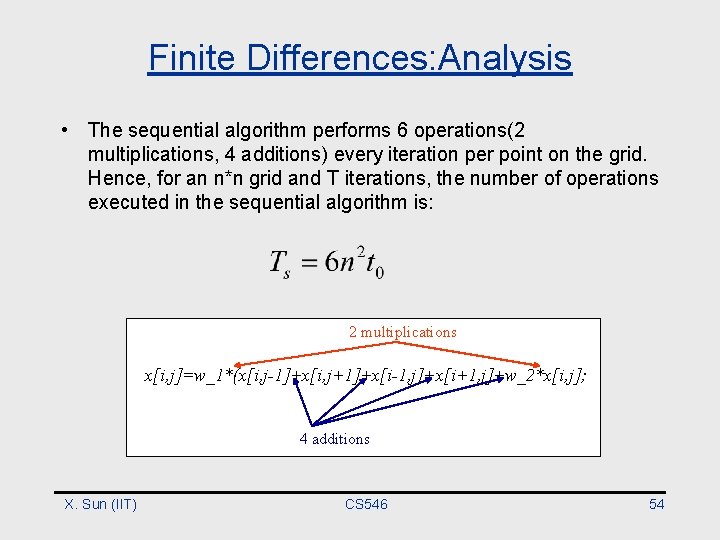
Finite Differences: Analysis • The sequential algorithm performs 6 operations(2 multiplications, 4 additions) every iteration per point on the grid. Hence, for an n*n grid and T iterations, the number of operations executed in the sequential algorithm is: 2 multiplications x[i, j]=w_1*(x[i, j-1]+x[i, j+1]+x[i-1, j]+x[i+1, j]+w_2*x[i, j]; 4 additions X. Sun (IIT) CS 546 54

Finite Differences: Analysis • The parallel algorithm uses p processors with static blockwise scheduling. Each processor computes on an m*m sub-grid allocated to each processor in a blockwise manner • The expression for m is given by The runtime for the parallel algorithm is: X. Sun (IIT) CS 546 55

Finite Differences: Analysis • The barrier synch needed for each iteration can be optimally performed in log(p) steps • The total runtime for the parallel algorithm for the computation is: • The speedup of the parallel algorithm is: X. Sun (IIT) CS 546 56

Finite Differences: Analysis • The Amdahl’s fraction for this parallel algorithm can be determined by rewriting the previous equation as: • Hence, the Amdahl’s fraction (n. p) is: • We finally note that • Hence, the parallel algorithm is effective X. Sun (IIT) CS 546 57

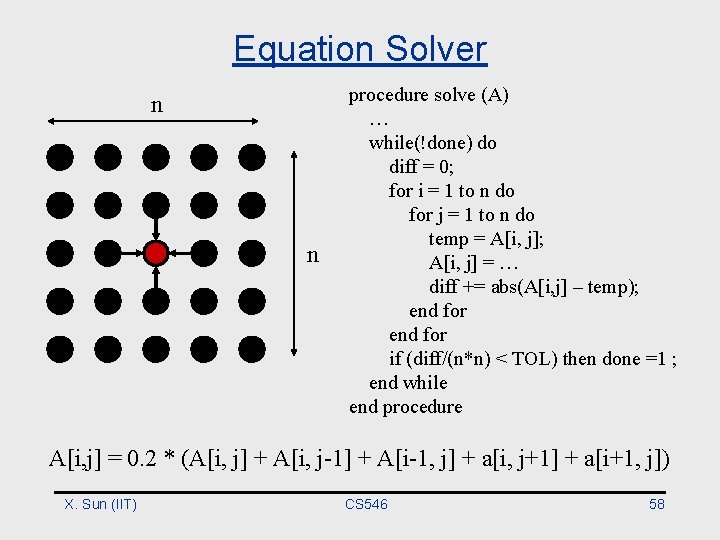
Equation Solver n n procedure solve (A) … while(!done) do diff = 0; for i = 1 to n do for j = 1 to n do temp = A[i, j]; A[i, j] = … diff += abs(A[i, j] – temp); end for if (diff/(n*n) < TOL) then done =1 ; end while end procedure A[i, j] = 0. 2 * (A[i, j] + A[i, j-1] + A[i-1, j] + a[i, j+1] + a[i+1, j]) X. Sun (IIT) CS 546 58

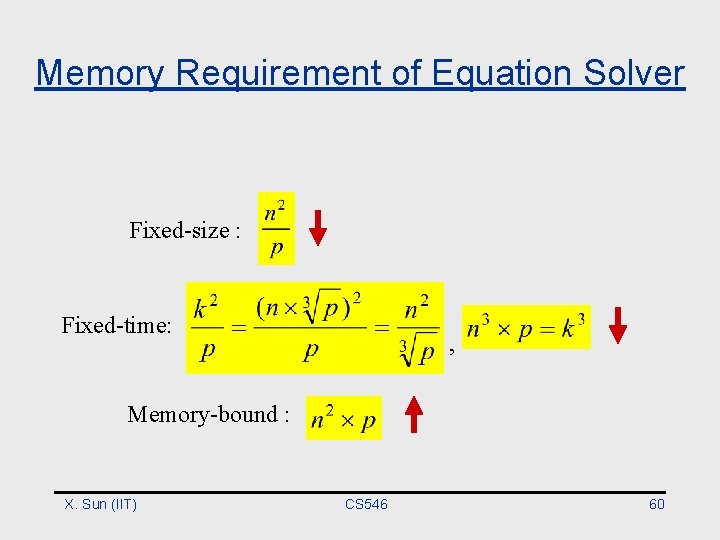
Workloads • Basic properties – Memory requirement : O(n 2) – Computational complexity : O(n 3), assuming the number of iterations to converge to be O(n) • Assume speedups equal to # of p • Grid size – Fixed-size : fixed – Fixed-time : – Memory-bound : X. Sun (IIT) CS 546 59

Memory Requirement of Equation Solver Fixed-size : Fixed-time: , Memory-bound : X. Sun (IIT) CS 546 60

Time Complexity of Equation Solver Fixed-size: Fixed-time: Memory-bound: Sequential time complexity , X. Sun (IIT) CS 546 61

Concurrency is proportional to the number of grid points Fixed-size : Fixed-time: , Memory-bound: X. Sun (IIT) CS 546 62

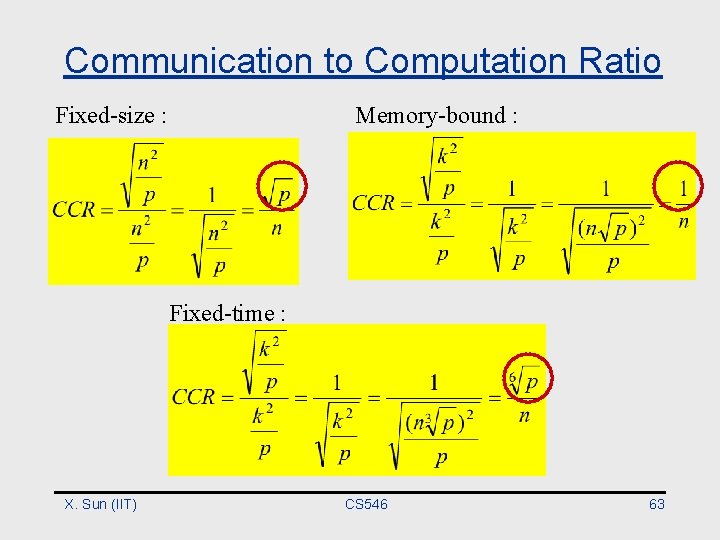
Communication to Computation Ratio Fixed-size : Memory-bound : Fixed-time : X. Sun (IIT) CS 546 63

Scalability • The Need for New Metrics • Comparison of performances with different workload • Availability of massively parallel processing • Scalability Ability to maintain parallel processing gain when both problem size and system size increase X. Sun (IIT) CS 546 64

Parallel Efficiency • The achieved fraction of total potential parallel processing gain – Assuming linear speedup p is ideal case • The ability to maintain efficiency when problem size increase X. Sun (IIT) CS 546 65

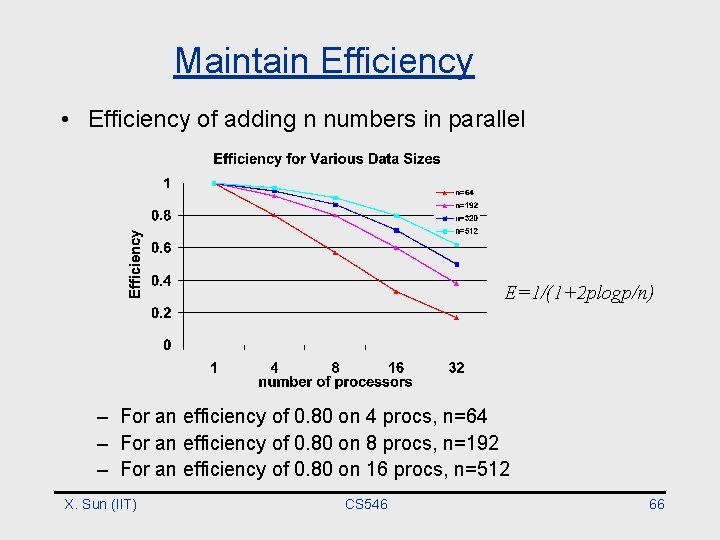
Maintain Efficiency • Efficiency of adding n numbers in parallel E=1/(1+2 plogp/n) – For an efficiency of 0. 80 on 4 procs, n=64 – For an efficiency of 0. 80 on 8 procs, n=192 – For an efficiency of 0. 80 on 16 procs, n=512 X. Sun (IIT) CS 546 66

• Ideally Scalable T(m p, m W) = T(p, W) – – – T: execution time W: work executed P: number of processors used m: scale up m times work: flop count based on the best practical serial algorithm • Fact: T(m p, m W) = T(p, W) if and only if The Average Unit Speed Is Fixed X. Sun (IIT) CS 546 67

– Definition: The average unit speed is the achieved speed divided by the number of processors – Definition (Isospeed Scalability): An algorithm-machine combination is scalable if the achieved average unit speed can remain constant with increasing numbers of processors, provided the problem size is increased proportionally X. Sun (IIT) CS 546 68

• Isospeed Scalability (Sun & Rover, 91) – W: work executed when p processors are employed – W': work executed when p' > p processors are employed to maintain the average speed – Ideal case – Scalability in terms of time X. Sun (IIT) CS 546 69

• Isospeed Scalability (Sun & Rover) – W: work executed when p processors are employed – W': work executed when p' > p processors are employed to maintain the average speed – Ideal case • X. H. Sun, and D. Rover, "Scalability of Parallel Algorithm-Machine Combinations, " IEEE Trans. on Parallel and Distributed Systems, May, 1994 (Ames TR 91) X. Sun (IIT) CS 546 70

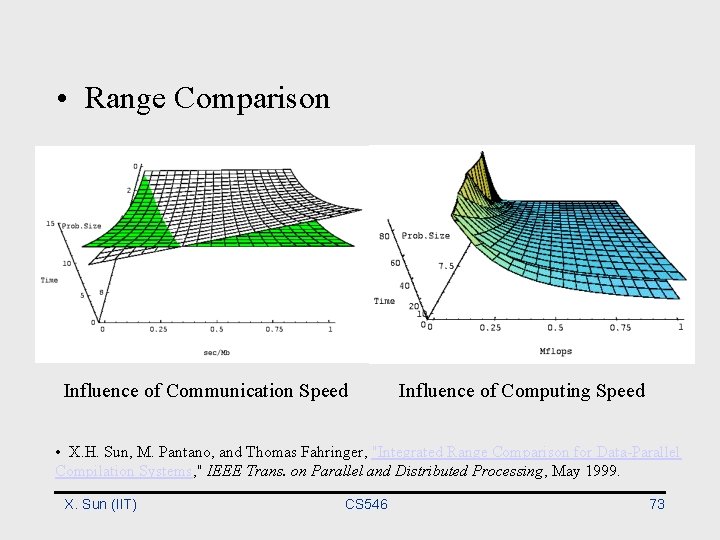
The Relation of Scalability and Time • More scalable leads to smaller time – Better initial run-time and higher scalability lead to superior run-time – Same initial run-time and same scalability lead to same scaled performance – Superior initial performance may not last long if scalability is low • Range Comparison • X. H. Sun, "Scalability Versus Execution Time in Scalable Systems, " Journal of Parallel and Distributed Computing, Vol. 62, No. 2, pp. 173 -192, Feb 2002. X. Sun (IIT) CS 546 71

Range Comparison Via Performance Crossing Point Assume Program I is oz times slower than program 2 at the initial state Begin (Range Comparison) p' = p; Repeat p' = p' + 1; Compute the scalability of program 1 (p, p'); Compute the scalability of program 2 (p, p') ; Until ( (p, p') > (p, p') or p'= the limit of ensemble size) If (p, p') > (p, p') Then p is the smallest scaled crossing point; program 2 is superior at any ensemble size p†, p p† < p' Else program 2 is superior at any ensemble size p†, p p† p’ End {if} End {Range Comparison} X. Sun (IIT) CS 546 72

• Range Comparison Influence of Communication Speed Influence of Computing Speed • X. H. Sun, M. Pantano, and Thomas Fahringer, "Integrated Range Comparison for Data-Parallel Compilation Systems, " IEEE Trans. on Parallel and Distributed Processing, May 1999. X. Sun (IIT) CS 546 73

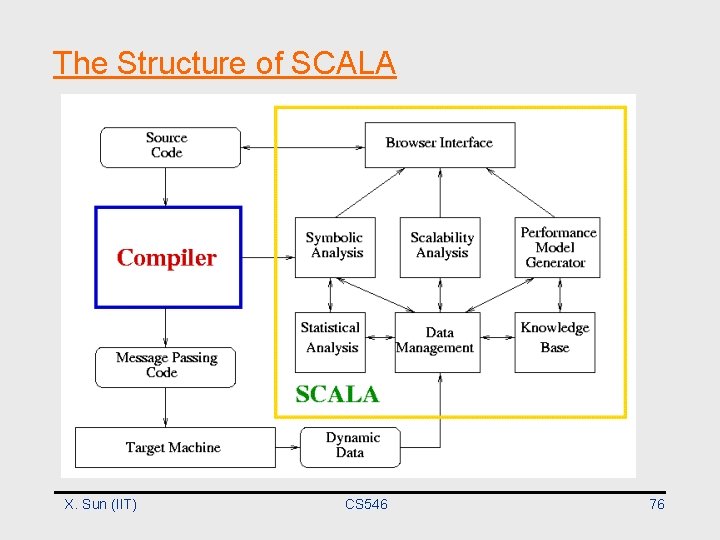
The SCALA (SCALability Analyzer) System • Design Goals – Predict performance – Support program optimization – Estimate the influence of hardware variations • Uniqueness – Designed to be integrated into advanced compiler systems – Based on scalability analysis X. Sun (IIT) CS 546 74

• Vienna Fortran Compilation System – A data-parallel restructuring compilation system – Consists of a parallelizing compiler for VF/HPF and tools for program analysis and restructuring – Under a major upgrade for HPF 2 • Performance prediction is crucial for appropriate program restructuring X. Sun (IIT) CS 546 75

The Structure of SCALA X. Sun (IIT) CS 546 76

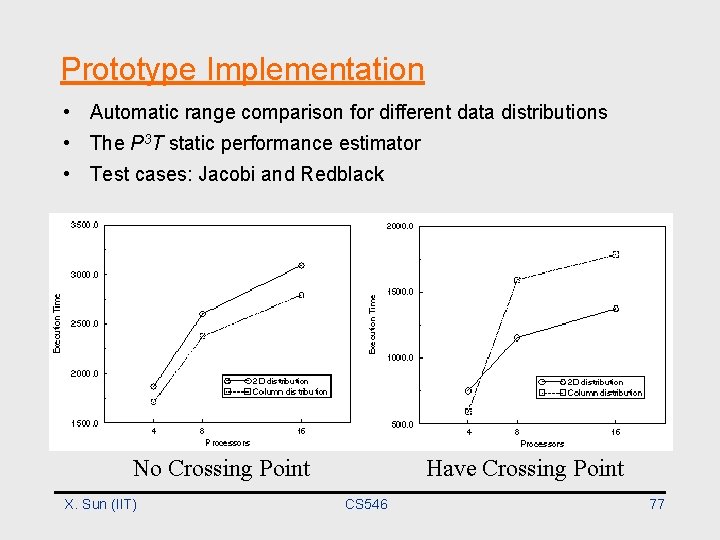
Prototype Implementation • Automatic range comparison for different data distributions • The P 3 T static performance estimator • Test cases: Jacobi and Redblack No Crossing Point X. Sun (IIT) Have Crossing Point CS 546 77

Summary • Relation between Iso-speed scalability and isoefficiency scalability – Both measure the ability to maintain parallel efficiency defined as – Where iso-efficiency’s speedup is the traditional speedup defined as – Iso-speed’s speedup is the generalized speedup defined as – If the sequential execution speed is independent of problem size, iso-speed and iso-efficiency is equivalent – Due to memory hierarchy, sequential execution performance varies largely with problem size X. Sun (IIT) CS 546 78

Summary • Predict the sequential execution performance becomes a major task of SCALA due to advanced memory hierarchy – Memory-Log. P model is introduced for data access cost • New challenge in distributed computing • Generalized iso-speed scalability • Generalized performance tool: GHS • K. Cameron and X. -H. Sun, "Quantifying Locality Effect in Data Access Delay: Memory log. P, " Proc. of 2003 IEEE IPDPS 2003, Nice, France, April, 2003. • X. -H. Sun and M. Wu, "Grid Harvest Service: A System for Long-Term, Application-Level Task Scheduling, " Proc. of 2003 IEEE IPDPS 2003, Nice, France, April, 2003. X. Sun (IIT) CS 546 79