Partial Redundancy Elimination PartialRedundancy Elimination n n Minimize

Partial Redundancy Elimination

Partial-Redundancy Elimination n n Minimize the number of expression evaluations By moving around the places where an expression is evaluated and keeping the result in a temporary variable when necessary, we often can reduce the number of evaluations of this expression along many of the execution paths, while not increasing that number along any path

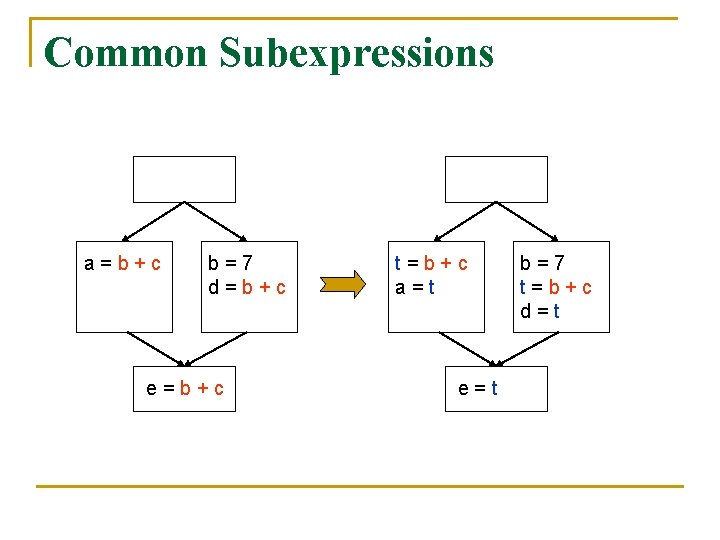
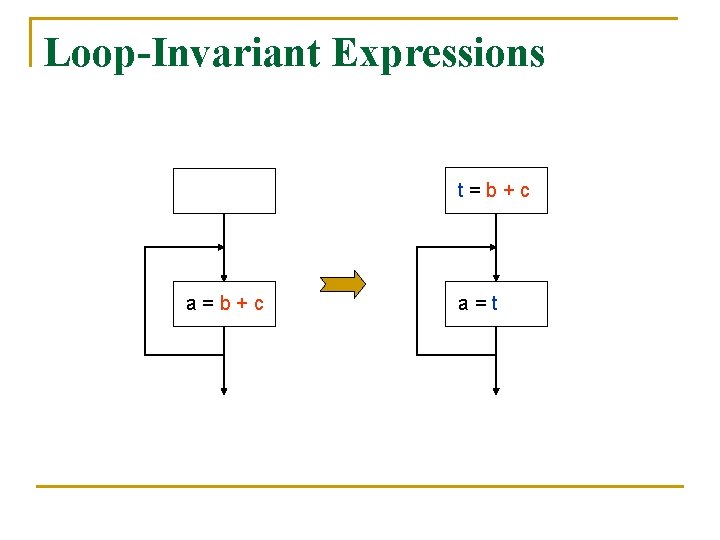
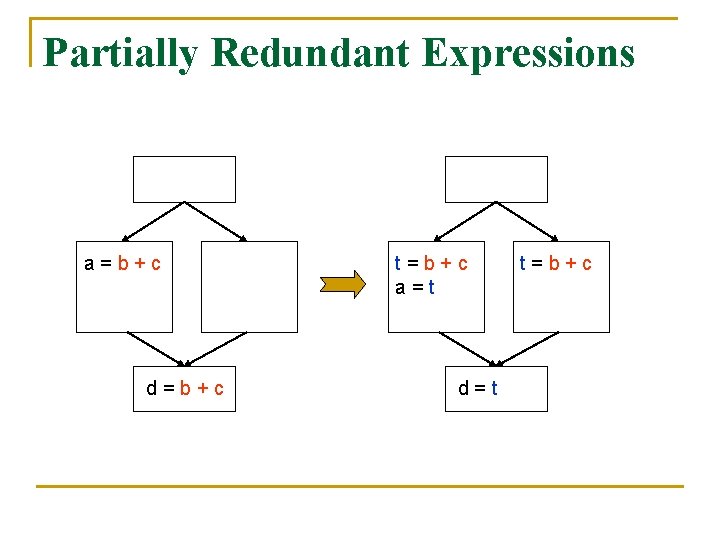
The Sources of Redundancy n n n Common subexpressions Loop-invariant expressions Partially redundant expressions

Common Subexpressions a=b+c b=7 d=b+c e=b+c t=b+c a=t e=t b=7 t=b+c d=t

Loop-Invariant Expressions t=b+c a=t

Partially Redundant Expressions a=b+c d=b+c t=b+c a=t d=t t=b+c

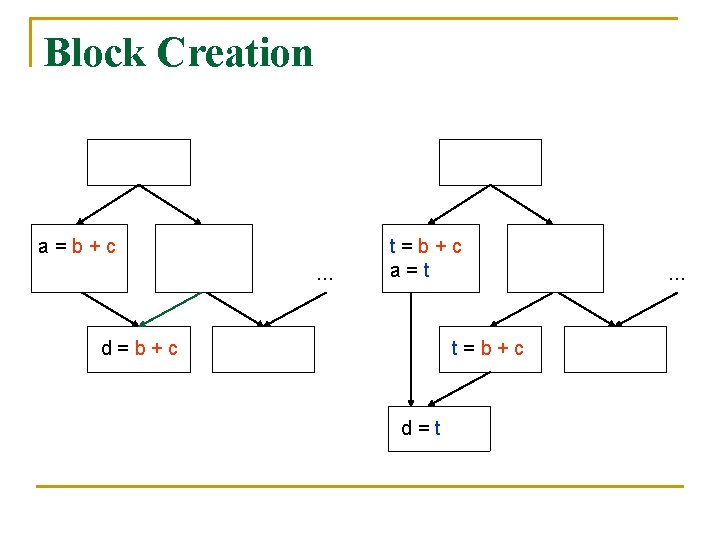
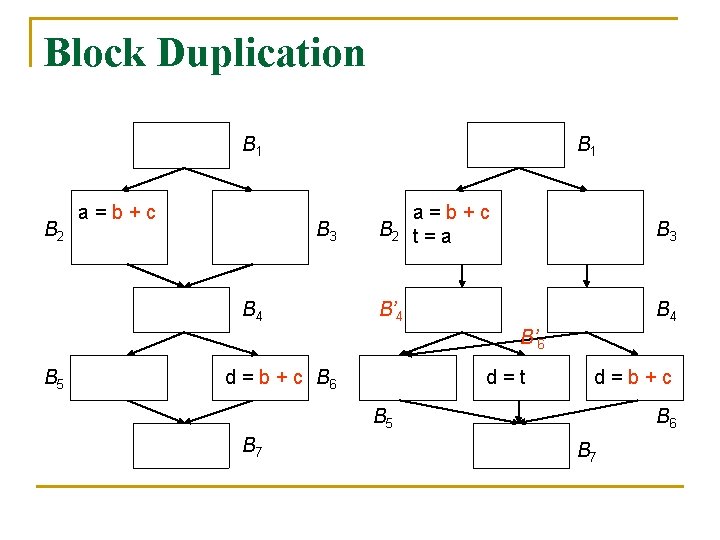
Can All Redundancy Be Eliminated? n n n It is not possible to eliminate all redundant computations along every path, unless we are allowed to change the control flow graph by creating new blocks and duplicating blocks A critical edge is an edge leading from a node with more than one successor to a node with more than one predecessor Block duplication can be used to isolate the path where redundancy is found

Block Creation a=b+c … t=b+c a=t d=b+c t=b+c d=t …

Block Duplication B 1 B 2 a=b+c B 3 B 4 B 2 a=b+c t=a B 3 B’ 4 B’ 6 B 5 d = b + c B 6 d=t d=b+c B 5 B 7 B 6 B 7

The Lazy-Code-Motion Problem n n Three properties desirable from the partial redundancy elimination algorithm All redundant computations of expressions that can be eliminated without block duplication are eliminated The optimized program does not perform any computation that is not in the original program execution Expressions are computed at the latest possible time

Lazy Code Motion n The values of expressions found to be redundant are usually held in registers until they are used Computing a value as late as possible minimizes its lifetime the duration between the time the value is defined and the time it is last used Minimizing the lifetime of a value in turn minimizes the usage of a register

Full Redundancy n n An expression e in block B is redundant if along all paths reaching B, e has been evaluated and the operands of e have not been redefined subsequently Let S be the set of blocks, each containing expression e, that renders e in B redundant The set of edges leaving the blocks in S must necessarily form a cutset, which if removed, disconnects B from the entry of the program No operands of e are redefined along the paths that lead from the blocks in S to B

Partial Redundancy n n If an expression e in block B is only partial redundant, the lazy code motion algorithm attempts to render e fully redundant in B by placing additional copies of the expressions in the flow graph If the attempt is successful, the optimized flow graph will also have a set of blocks S, each containing e, and whose outgoing edges are a cutset between the entry and B

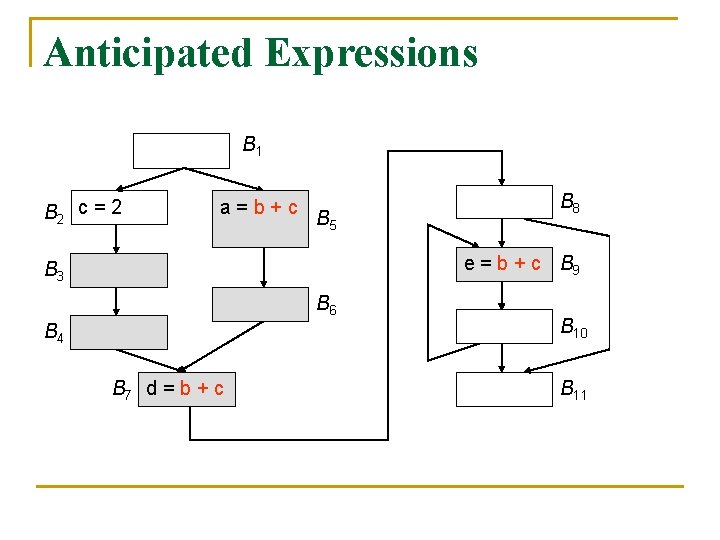
Anticipation of Expressions n n To ensure that no extra operations are executed, copies of an expression must be placed only at program points where the expression is anticipated (very busy) An expression e is anticipated at point p if all paths leading from p eventually compute the value of e using the values of operands that are available at p

Earliest Places of Expressions n n n Consider an acyclic path B 1 B 2 … Bn Suppose e is evaluated only in blocks B 1 and Bn, and the operands of e are not redefined in blocks along the path. There are incoming edges that join the path and there are outgoing edges that exit the path Expression e is not anticipated at the entry of Bi iff there exists an outgoing edge leaving Bj, i j < n, that leads to an execution path that does not use the value of e

Earliest Placement of Expressions B 1 … Bj … Bn … n Anticipation limits how early an expression can be placed

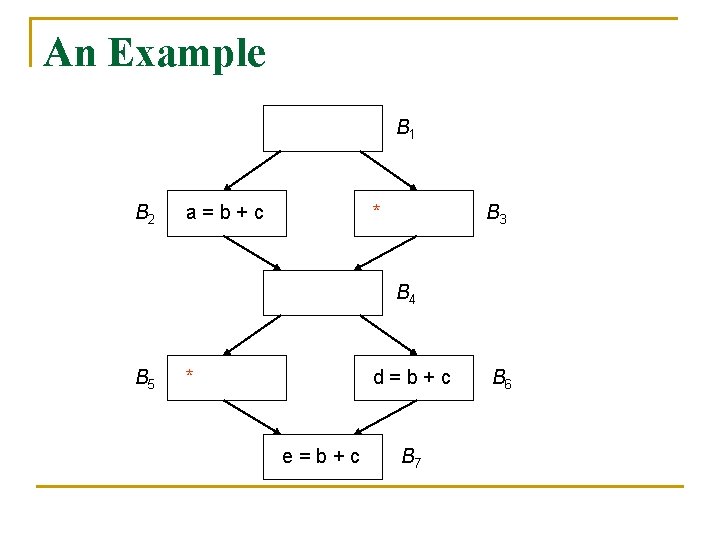
Earliest Placement of Expressions n n We can create a cutset that includes the edge Bi-1 Bi and that renders e redundant in Bn if e is either available or anticipated at the entry of Bi If e is anticipated but not available at the entry of Bi, we must place a copy of e along the incoming edge

Earliest Placement of Expressions n n The introduced expressions may themselves be partially redundant with other instances of the same expression Such partial redundancy may be eliminated by moving these computations further up

An Example B 1 B 2 a=b+c * B 3 B 4 B 5 * d=b+c e=b+c B 7 B 6

Latest Placement of Expressions n n We have a choice of where to place the copies of e, since there are usually several cutsets in the flow graph that satisfy all the requirements Computation is introduced along the incoming edges to the path so the expression is computed as close to the use as possible without introducing redundancy

Summary n n n Anticipation limits how early an expression can be placed The earlier an expression is placed, the more redundancy can be removed Among all solutions that eliminate the same redundancies, the one that computes the expressions the latest minimizes the lifetime of the register holding the values of the expressions involved

The Lazy-Code-Motion Algorithm n n Find all the expressions anticipated at each program point using a backward analysis Find all the expressions available at each program point using a forward analysis. Find all the expressions postponable at each program point using a forward analysis Find all the expressions used at each program point using a backward analysis

Preprocessing n n n Assume that initially every statement is in a basic block of its own, and we only introduce new computations of expressions at the beginning of blocks To ensure that this simplification does not reduce the effectiveness of the technique, we insert a new block between the source and the destination of an edge if the destination has more than one predecessor This also takes care of all critical edges

e-use and e-kill Sets n n e-use. B is the set of expressions computed in B e-kill. B is the set of expressions any of whose operands are defined in B

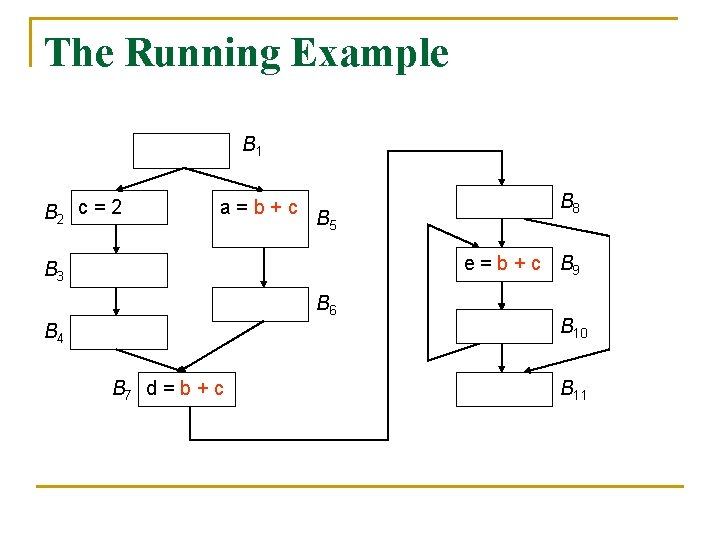
The Running Example B 1 B 2 c = 2 a=b+c B 5 B 8 e = b + c B 9 B 3 B 6 B 4 B 7 d = b + c B 10 B 11

Anticipated Expressions Direction Transfer function Boundary Meet( ) Equations Backwards f. B(x) = e_use. B (x – e_kill. B) IN[EXIT] = IN[B] = f. B(OUT[B]) OUT[B] = s, succ(B) IN[S] Initialization IN[B] = U

Anticipated Expressions B 1 B 2 c = 2 a=b+c B 5 B 8 e = b + c B 9 B 3 B 6 B 4 B 7 d = b + c B 10 B 11

Available Expressions Direction Transfer function Boundary Meet( ) Equations Forwards f. B(x) = (anticipated[B]. in x) – e_kill. B OUT[ENTRY] = OUT[B] = f. B(IN[B]) IN[B] = P, pred(B) OUT[P] Initialization OUT[B] = U

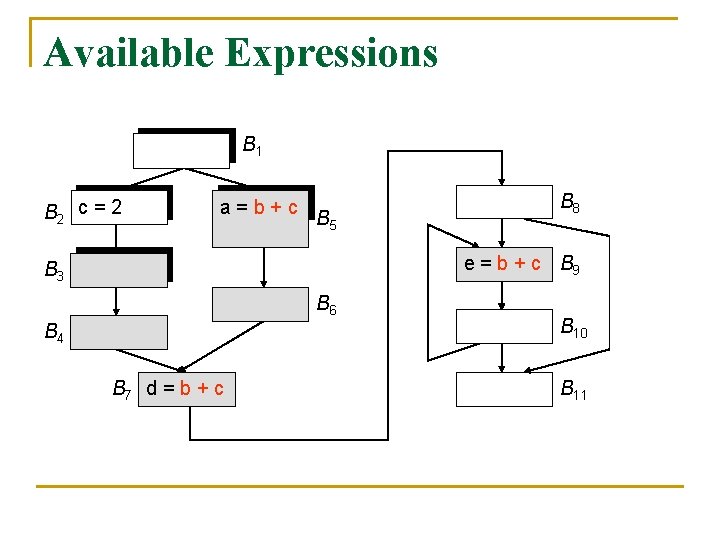
Available Expressions B 1 B 2 c = 2 a=b+c B 5 B 8 e = b + c B 9 B 3 B 6 B 4 B 7 d = b + c B 10 B 11

Available Expressions B 1 a = b + c B 2 B 3 d = b + c B 4

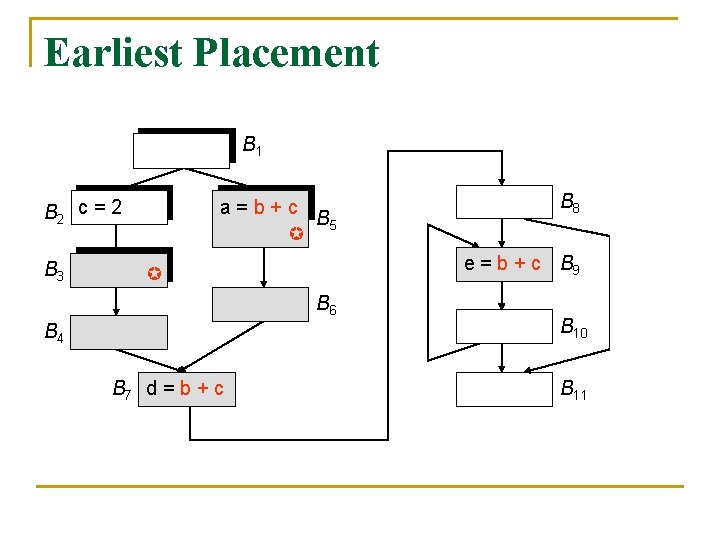
Earliest Placement n With the earliest placement strategy, the set of expressions placed at block B, i. e. , earliest[B], is defined as the set of anticipated expressions that are not yet available earliest[B] = anticipated[B]. in – available[B]. in

Earliest Placement B 1 B 2 c = 2 B 3 a=b+c B 5 e = b + c B 9 B 6 B 4 B 7 d = b + c B 8 B 10 B 11

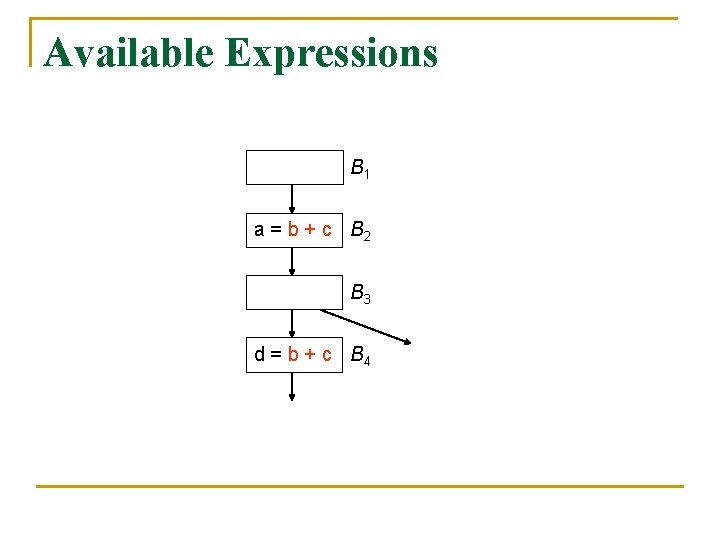
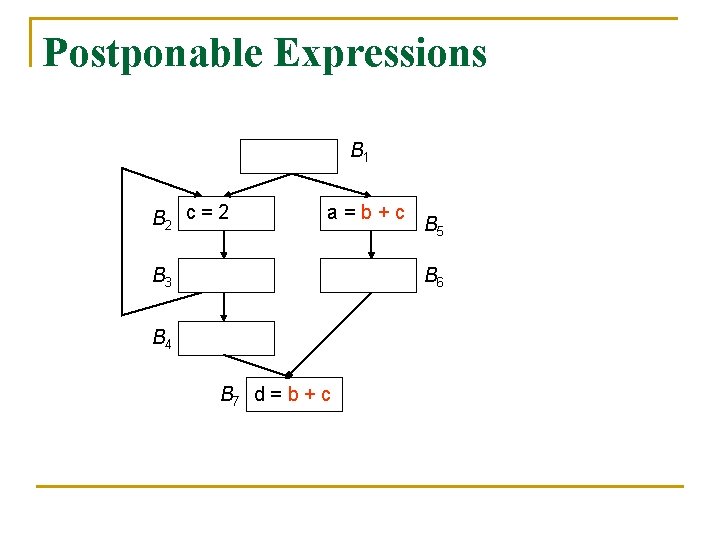
Postponable Expressions B 1 B 2 c = 2 a=b+c B 3 B 5 B 6 B 4 B 7 d = b + c

Postponable Expressions Direction Transfer function Boundary Meet( ) Equations Forwards f. B(x) = (earliest[B] x) – e_use. B OUT[ENTRY] = OUT[B] = f. B(IN[B]) IN[B] = P, pred(B) OUT[P] Initialization OUT[B] = U

Postponable Expressions B 1 B 2 c = 2 a=b+c B 5 B 8 e = b + c B 9 B 3 B 6 B 4 B 7 d = b + c B 10 B 11

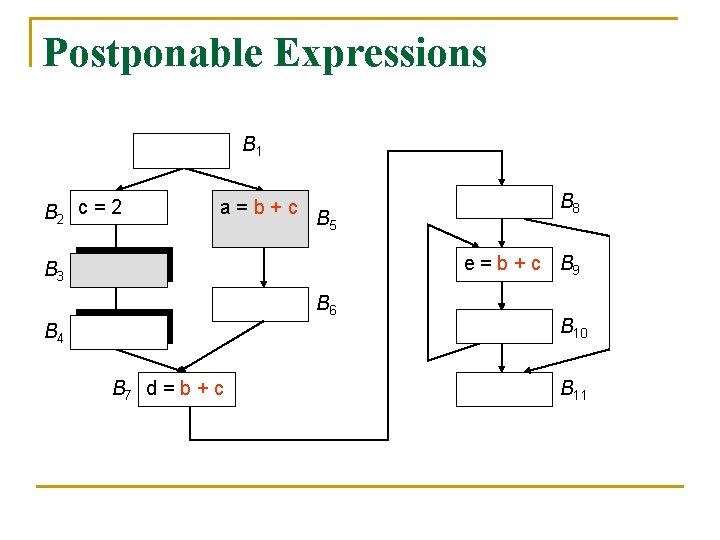
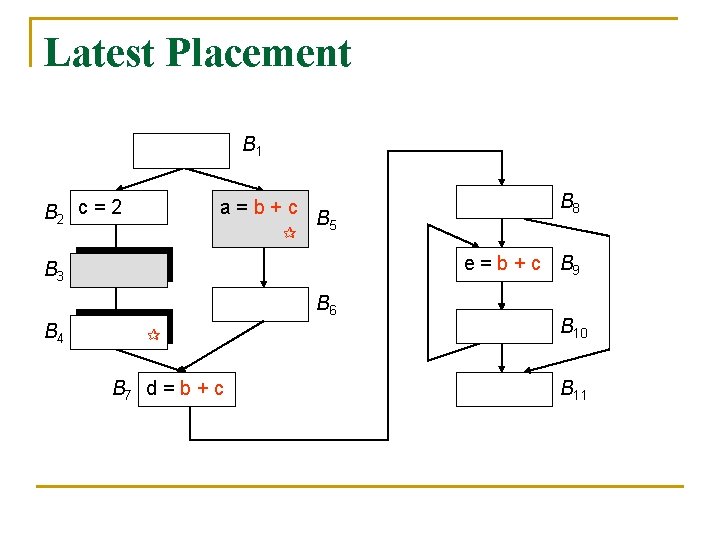
Latest Placement n n Expression e may be placed at the beginning of a block B only if e is in B’s earliest or postponable set upon entry In addition, B is in the postponement frontier of e if one of the following holds: e is in e_use. B e cannot be postponed to one of its successors, i. e. , e is not in the earliest or postponable set upon entry to that successor

Latest Placement latest[B] = (earliest[B] postponable[B]. in) (e_use. B ( S, succ(B)(earliest[S] postponable[S]. in)))

Latest Placement B 1 B 2 c = 2 a=b+c B 5 e = b + c B 9 B 3 B 6 B 4 B 8 B 7 d = b + c B 10 B 11

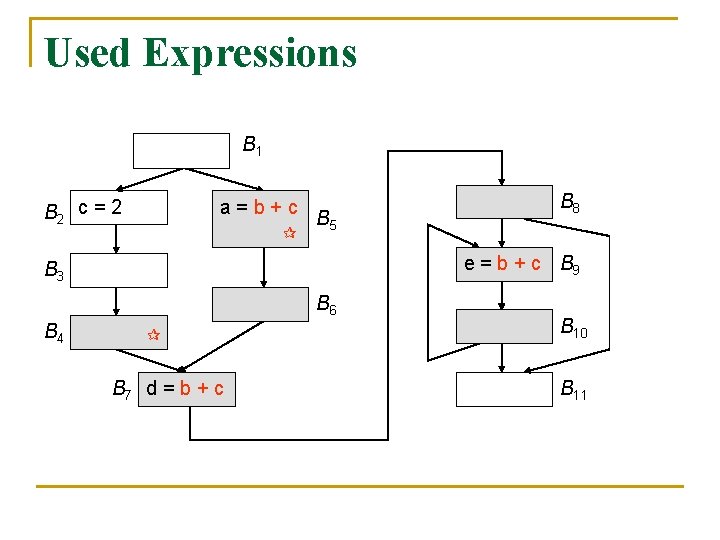
Used Expressions Direction Transfer function Boundary Meet( ) Equations Backwards f. B(x) = (e_use. B x) – latest[B] IN[EXIT] = IN[B] = f. B(OUT[B]) OUT[B] = s, succ(B) IN[S] Initialization IN[B] =

Used Expressions B 1 B 2 c = 2 a=b+c B 5 e = b + c B 9 B 3 B 6 B 4 B 8 B 7 d = b + c B 10 B 11

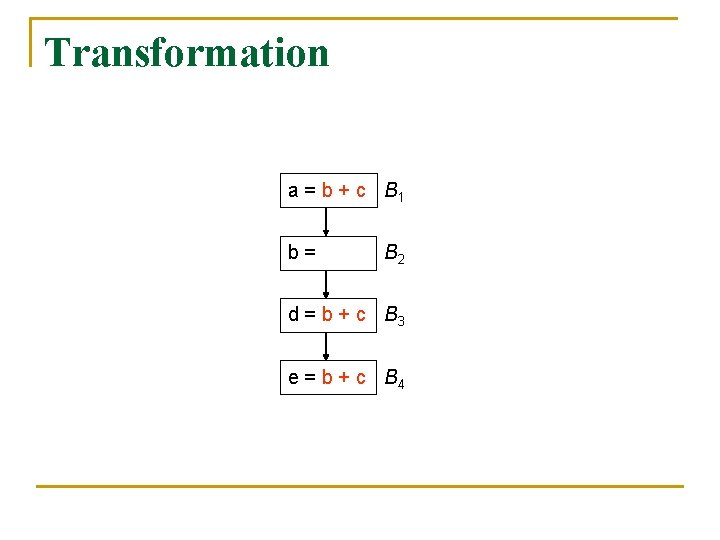
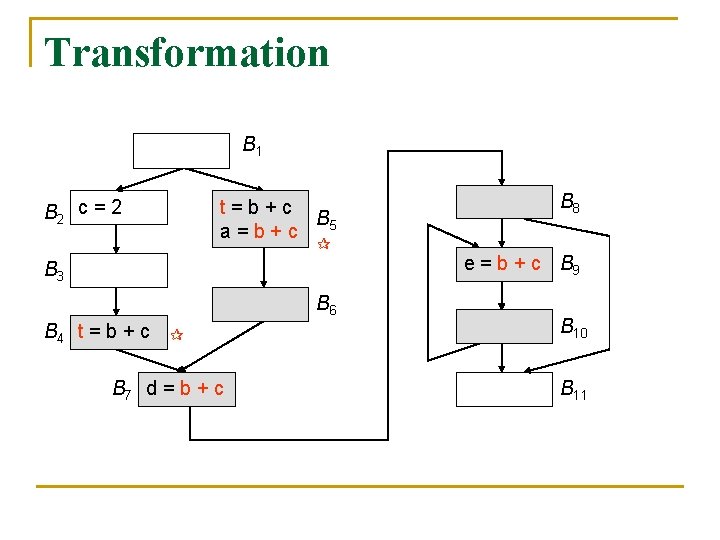
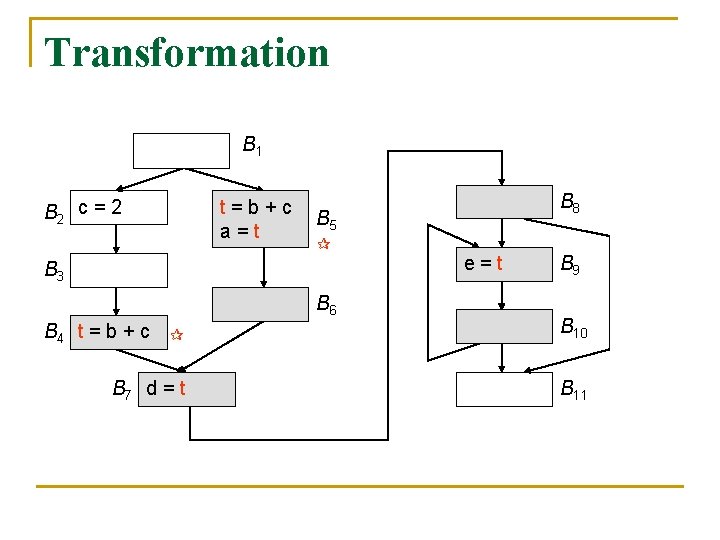
Transformation n n For each expression, say x + y, computed by the program, do the following: Create a new temporary, say t, for x + y For all blocks B such that x + y is in latest[B] used[B]. out, add t = x + y at the beginning of B For all blocks B such that x + y is in e_use. B ( latest[B] used[B]. out), replace every original x + y by t

Transformation a = b + c B 1 b= B 2 d = b + c B 3 e = b + c B 4

Transformation B 1 B 2 c = 2 t=b+c B 5 a=b+c B 3 B 6 B 4 t = b + c B 7 d = b + c B 8 e = b + c B 9 B 10 B 11

Transformation B 1 B 2 c = 2 t=b+c a=t B 8 B 5 B 3 B 6 e=t B 9 B 4 t = b + c B 10 B 7 d = t B 11