Otomata Teori Bahasa Pendahuluan Firrar Utdirartatmo Teori Bahasa

Otomata & Teori Bahasa Pendahuluan Firrar Utdirartatmo: Teori Bahasa dan Otomata JJ Learning Yogyakarta, erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Deskripsi OTB Otamata dan Teori Bahasa (OTB) matakuliah wajib n Komponen utama dari Ilmu Komputer yaitu model dan gagasan mendasar mengenai komputasi. n Suatu bentuk yang memiliki fungsi-fungsi dari komputer digital, menerima input, menghasilkan output, bisa memiliki penyimpanan sementara, dan mampu membuat keputusan dalam menstransformasikan dari input ke output n erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Outcome Pembelajaran Setelah memenuhi tujuan pembelajaran mata kuliah ini mahasiswa diharapkan : n Mampu memahami pengertian dari otomata dan teori bahasa. n Mampu memparaktekkan teori otomata dan teori bahasa dalam kehidupan sehari-hari n erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Introduction Erwin Yudi Hidayat n Teknik Informatika – S 1 n Bidang kajian: n n n Software Engineering and Intelligence Email: erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Komponen Penilaian Tugas n Ujian Tengah Semester n Ujian Akhir Semester n n : % : % Peraturan: Keterlambatan max n Ijin menggunakan surat n Dilarang mempresensikan n erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Referensi Firrar Utdirartatmo, Teori Bahasa dan Otomata, JJ Learning Yogyakarta, 2001 n Bambang Hariyanto, Teori Bahasa, Otomata, dan Komputasi serta Terapannya, Informatika Bandung, 2004 n Dean Kelley, Otomata dan Bahasa-bahasa Formal, PT. Prenhallindo, Jakarta, 1999 n n pppps: Slide bukan referensi atau materi XD erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Standar Kompetensi n Mahasiswa memahami pengertian dan kedudukan OTB pada ilmu komputer erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Contents 1 Definisi dan Pengertian 2 Kedudukan OTB 3 Tata Bahasa 4 Klasifikasi Tata Bahasa erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

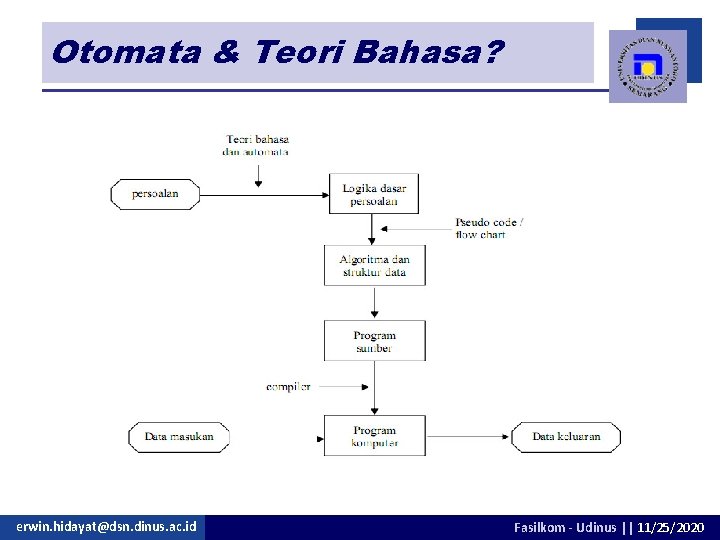
Otomata & Teori Bahasa? Bagian dari teori komputasi pada ilmu komputer n model matematika yang memiliki fungsi dari komputer digital yaitu menerima input, menghasilkan output, bisa memiliki penyimpanan sementara dan mampu membuat keputusan dalam transformasi input ke output n Penekanannya adalah pada pemecahan masalah n erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Otomata & Teori Bahasa? erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Kedudukan OTB n Ilmu komputer memiliki dua komponen utama: Pertama: model dan gagasan mendasar mengenai komputasi n Kedua: teknik rekayasa untuk perancangan sistem komputasi, meliputi perangkat keras dan perangkat lunak, khususnya penerapan rancangan dari teori. n n Otomata dan Teori Bahasa merupakan bagian pertama erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

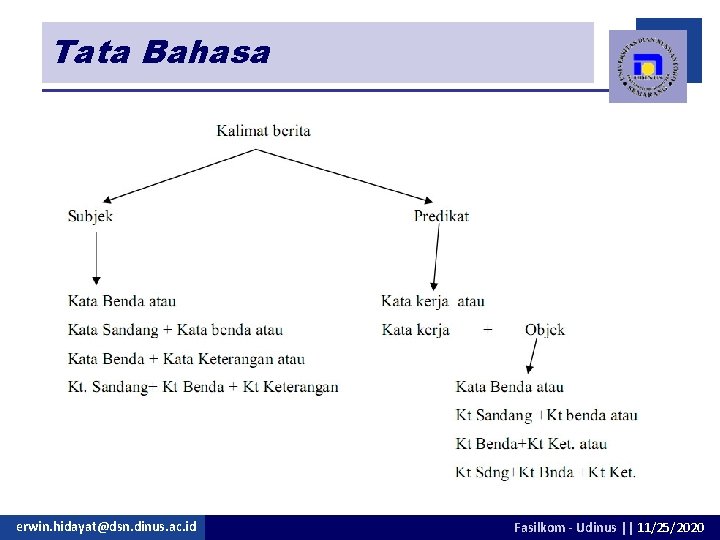
Tata Bahasa Penulisan suatu kalimat dalam sebuah bahasa, akan mengikuti suatu aturan tertentu yang berlaku pada bahasa tersebut n Aturan tersebut dikenal sebagai Tata Bahasa (Grammar) n erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Tata Bahasa erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

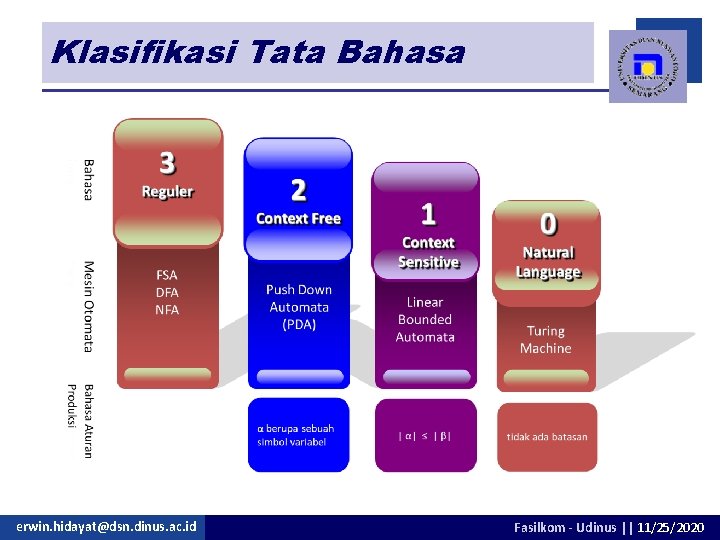
Klasifikasi Tata Bahasa Tata bahasa (grammar): kumpulan dari himpunan-himpunan variabel, simbol-simbol terminal, simbol awal yang dibatasi oleh aturan produksi. n Pada tahun 1959 seorang ahli bernama Noam Chomsky melakukan penggolongan tingkatan bahasa menjadi empat, yang disebut dengan Hirarki Chomsky. n erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Klasifikasi Tata Bahasa erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Konsep Bahasa n n n Abjad String Bahasa (Language) Bahasa Kosong Bahasa Universal dari ∑ erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Konsep Bahasa n Abjad Sebuah himpunan berhingga tak kosong dari simbol – simbol. n Notasi : ∑ n ∑ = {a, b, c, . . . , x, y, z} (Roman alphabet) o ∑ = {0, 1, . . . , 9} o ∑ = {0, 1} (binary alphabet) o erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Konsep Bahasa n Bahasa (Language) n Kumpulan dari string. Notasi : L ∑ = {1, 2, 3, 4, 5}, o Kumpulan {1, 123, 12345, 112} adalah bahasa dari abjad tersebut o ∑ = {1}, o Kumpulan {1, 111, 1111, …} adalah sebuah bahasa. o n Bahasa Kosong n Suatu bahasa yang tidak terdiri dari string. Notasi : {} atau Ø erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Konsep Bahasa n Bahasa universal dari ∑ Bahasa yang terdiri dari semua string berdasarkan suatu abjad ∑ n Notasi ∑* n ∑ = {1}, maka ∑* = {ɛ, 1, 111, 1111, …} n erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

Konsep Bahasa n Operasi-operasi pada Bahasa n n n n Concatenation Eksponensial Union (Gabungan) Intersection (Irisan) Sub Set (Sub Bahasa) Equal Closure Language erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

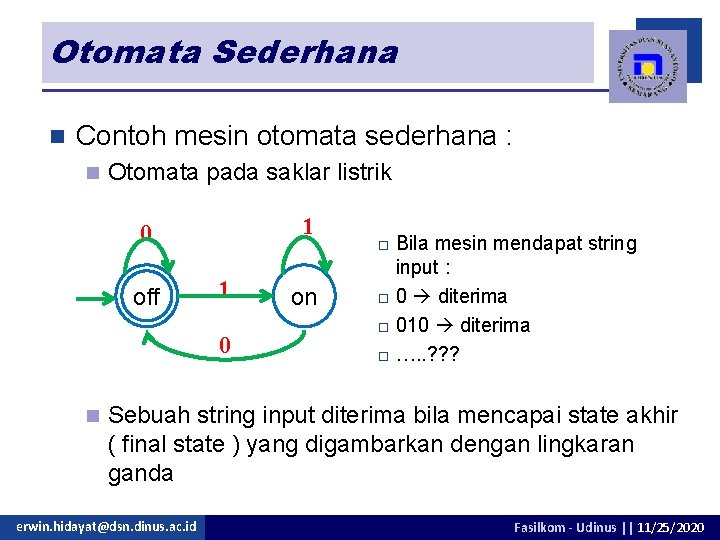
Otomata Sederhana n Contoh mesin otomata sederhana : n Otomata pada saklar listrik 1 0 off 1 0 n on Bila mesin mendapat string input : o 0 diterima o 010 diterima o …. . ? ? ? o Sebuah string input diterima bila mencapai state akhir ( final state ) yang digambarkan dengan lingkaran ganda erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

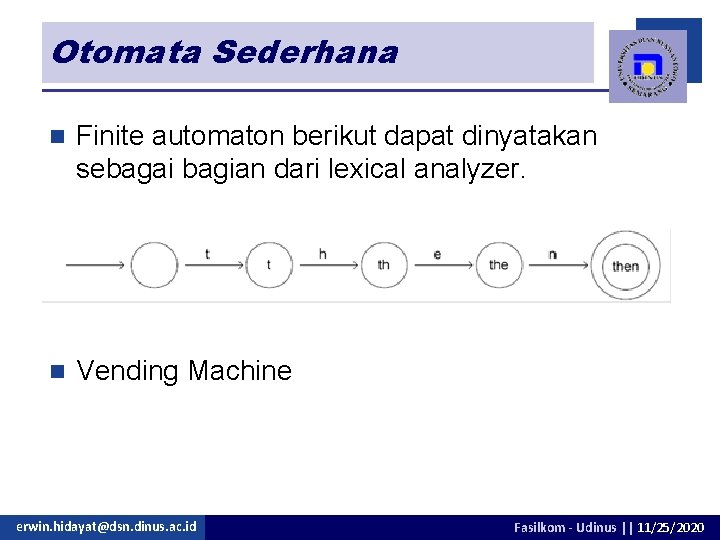
Otomata Sederhana n Finite automaton berikut dapat dinyatakan sebagai bagian dari lexical analyzer. n Vending Machine erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020

erwin. hidayat@dsn. dinus. ac. id Fasilkom - Udinus || 11/25/2020