SEMESTER PENDEK 20152016 OTOMATA DAN TEORI BAHASA FORMAL

SEMESTER PENDEK 2015/2016 OTOMATA DAN TEORI BAHASA FORMAL Betha Nurina Sari, M. Kom

PERTEMUAN 6 Pertemuan 11 : Pohon Penurunan Bebas Konteks q

Tata Bahasa Bebas Konteks (Context Free Grammar/CFG) Bahasa bebas konteks menjadi dasar dalam pembentukan suatu parser/proses analisis sintaksis. Bagian sintaks dalam suatu kompilator kebanyakan didefinisikan dalam tata bahasa bebas konteks. Bila pada tata bahasa regular terdapat pembatasan pada ruas kanan atau hasil produksinya, maka pada tata bahasa bebas konteks/context free grammar, selanjutnya kita sebut CFG, tidak terdapat pembatasan hasil produksinya. Pada aturan produksi:

Tata Bahasa Bebas Konteks (Context Free Grammar/CFG) Batasannya hanyalah ruas kiri (a) adalah sebuah simbol variabel. Contoh aturan produksi yang termasuk CFG : B–>CDe. Fg D–>Bc. De

PARSING Sebuah pohon (tree) adalah : suatu graph terhubung tidak sirkuler, yang memiliki satu simpul (node) /vertex yang disebut akar (root) dan dari root memiliki lintasan ke setiap simpul. Pohon penurunan (derivation tree/parse tree) berguna untuk menggambarkan bagaimana memperoleh suatu string (untai) dengan cara menurunkan simbol-simbol terminal. Setiap simbol variabel akan diturunkan menjadi terminal, sampai tidak ada yang belum tergantikan.

Contoh 1 Misalnya terdapat tata bahasa bebas konteks dengan aturan produksi (simbol awal S, selanjutnya digunakan sebagai simbol awal untuk tata bahasa bebas konteks adalah S). S –> AB A –> a. A | a B –> b. B | b

Akan kita gambarkan pohon penurunan untuk memperoleh untai : ‘aabbb’. Pada pohon tersebut simbol awal akan menjadi akar (root). Setiap kali penurunan dipilih aturan produksi yang menuju ke solusi. Simbol-simbol variabel akan menjadi simpul yang mempunyai anak. Simpul-simpul yang tidak mempunyai anak akan menjadi simbol terminal. Kalau kita baca simbol terminal yang ada pada gambar dari kiri kekanan akan diperoleh untai ‘aabbb’ :
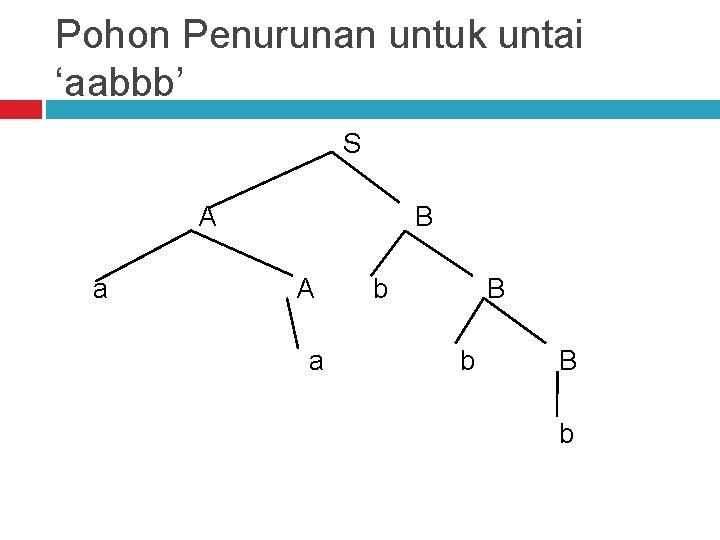
Pohon Penurunan untuk untai ‘aabbb’ S A a B A a b B b

Proses penurunan atau parsing bisa dilakukan dengan cara sebagai berikut Penurunan terkiri (leftmost derivation) : simbol variabel terkiri yang diperluas terlebih dahulu Penurunan terkanan ( rightmost derivation) : simbol variabel terkanan yang diperluas terlebih dahulu

Contoh 2 Misal, terdapat tata bahasa bebas konteks : S –> a. AS | a A –> Sb. A | ba Untuk memperoleh untai ‘aabbaa’ dari tata bahasa bebas konteks diatas (‘=>’ bisa dibaca ‘menurunkan’): Dengan penurunan terkiri: S => a. AS => a. Sb. AS => aabbaa, Dengan penurunan terkanan : S => a. AS=> a. Aa=>a. Sbbaa=>aabbaa. Kita dapat melihat pohon penurunannya pada gambar meskipun proses penurunannya berbeda, namun akan tetap memiliki pohon penurunan yang sama.
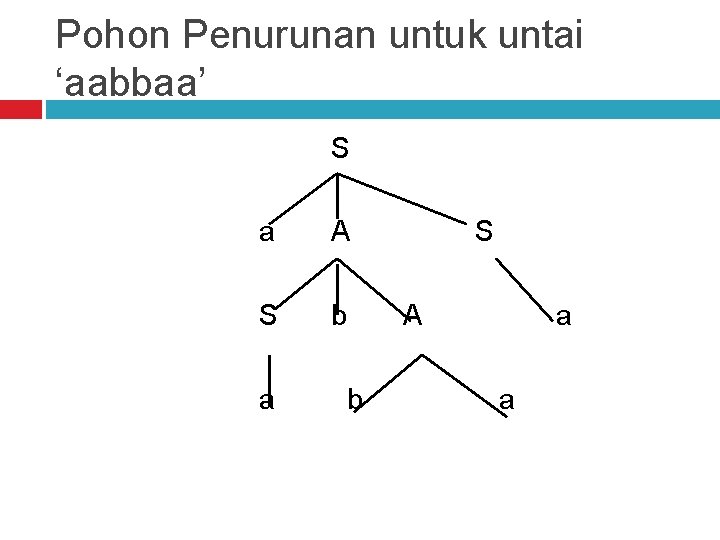
Pohon Penurunan untuk untai ‘aabbaa’ S a A S b a b S A a a

Contoh 3 Biasanya persoalan yang diberikan berkaitan dengan pohon penurunan adalah untuk mencari penurunan yang hasilnya menuju kepada suatu untai yang ditentukan. Dalam hal ini, perlu untuk melakukan percobaan pemilihan aturan produksi yang bisa menuju ke solusi. Misalnya sebuah tata bahasa bebas konteks memiliki aturan produksi sebagai berikut. S –> a. B | b. A A –> a | a. S | b. AA B –> b | b. S | Abb Buat pohon penurunan untuk memperoleh ‘aaabbabbba’
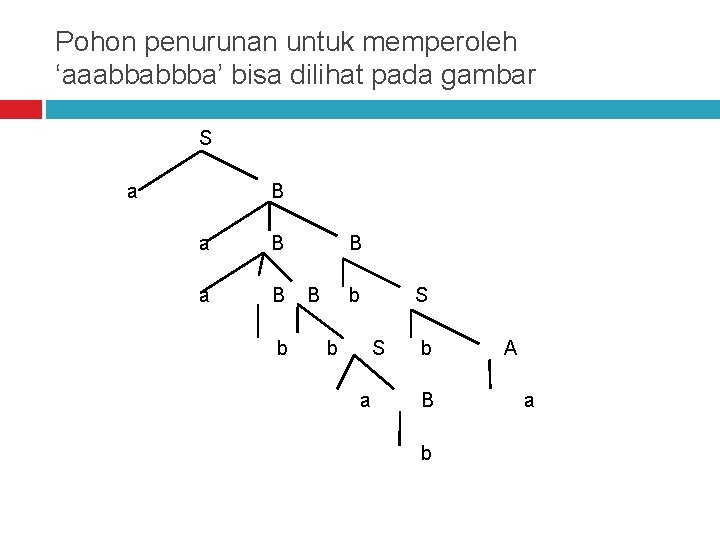
Pohon penurunan untuk memperoleh ‘aaabbabbba’ bisa dilihat pada gambar S a B a B b B B b S a b B b A a
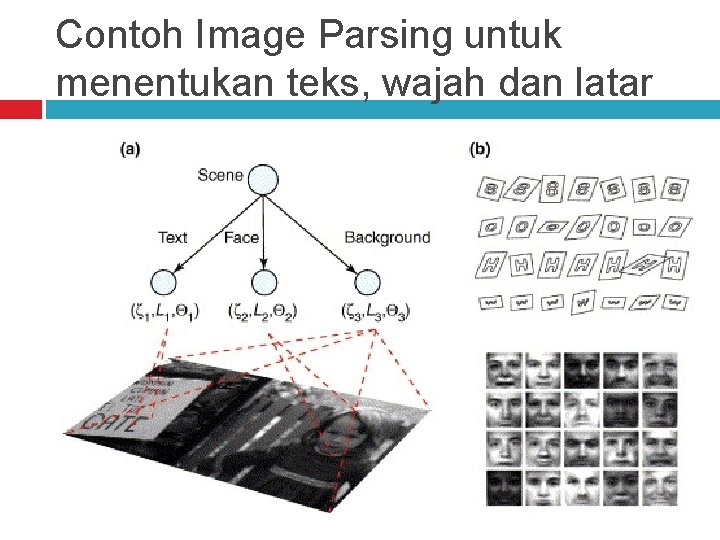
Contoh Image Parsing untuk menentukan teks, wajah dan latar
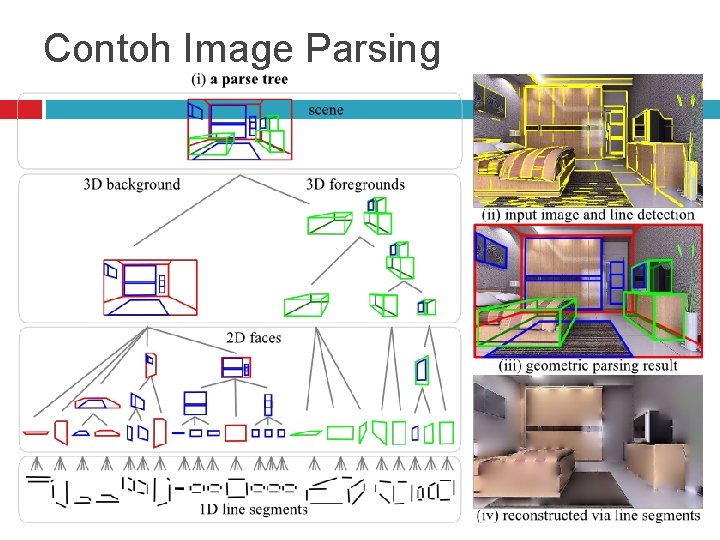
Contoh Image Parsing

Contoh Image Parsing Fungsinya : proses parsing image untuk memahami suatu gambar menjadi 4 aspek perhitungan ruang. 1. Menghitung 3 D scene layout 2. Deteksi obyek 3 D. c/: Furniture 3. Deteksi obyek 2 D. c/: Jendela, Pintu 4. Segmentasi backround

AMBIGUITAS Ambiguitas/ke-dwi artian terjadi bila terdapat lebih dari satu pohon penurunan yang berbeda untuk memperoleh suatu untai. Misalkan terdapat tata bahasa bebas konteks : S–>A|B A–>a B–>a Untuk memperoleh untai ‘a’ bisa terdapat dua cara penurunan berikut ini. S=>A=>a S=>B=>a

AMBIGUITAS Contoh yang lain, terdapat tata bahasa bebas konteks : S–>Sb. S | Sc. S | a Kita bisa menurunkan untai ‘abaca’ dalam dua cara berikut ini 1. S=>Sb. S => Sb. Sca => Sbaca => abaca 2. S=>Sc. S => Sb. Sc. S => abaca
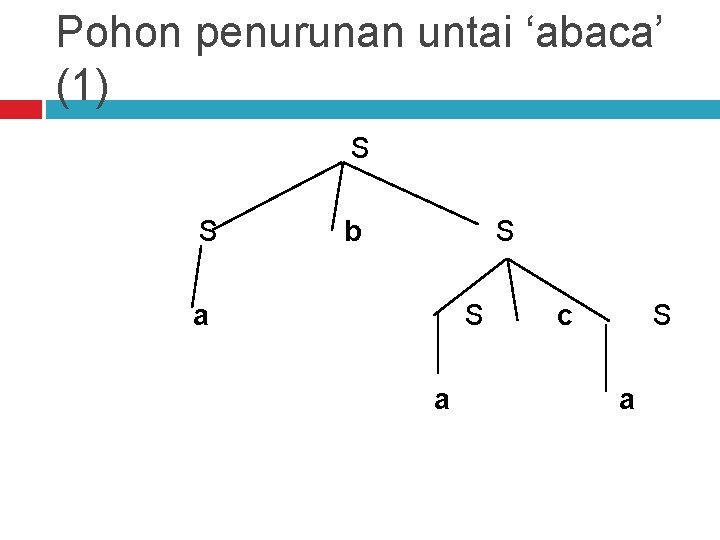
Pohon penurunan untai ‘abaca’ (1) S S b S a c S a
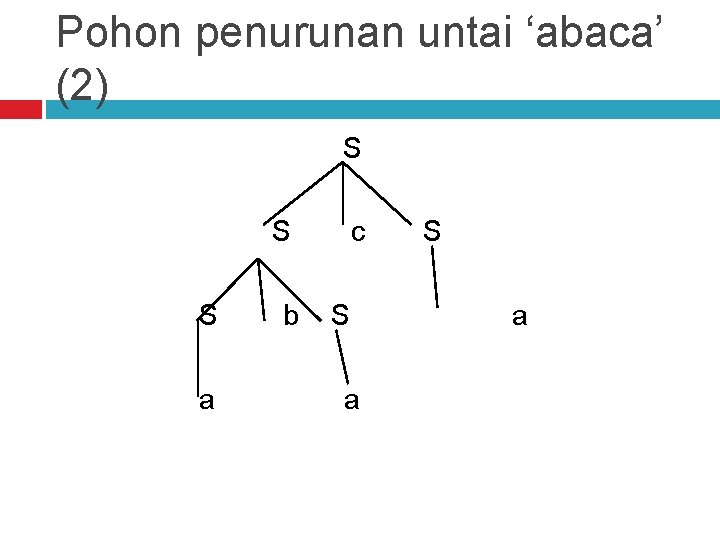
Pohon penurunan untai ‘abaca’ (2) S S S a b c S a

AMBIGUITAS Ambiguitas dapat menimbulkan masalah pada bahasa-bahasa tertentu, baik bahasa alami maupun pada bahasa pemrograman. Bila suatu struktur bahasa memiliki lebih dari suatu dekomposisi (penurunan), dan susunannya akan menentukan arti, maka artinya menjadi ambigu

Pohon Penurunan Kita bisa melihat bahwa untuk untai yang sama (‘abaca’) dapat dibuat pohon penurunan yang berbeda, maka bahwa dapat dikatakan tata bahasa bebas konteks tersebut ambigu. Jadi, untuk menunjukan bahwa suatu tata bahasa bebas konteks ambigu, bisa dilakukan dengan menemukan untai yang memungkinkan pembentukan lebih dari satu pohon penurunan.

PERTEMUAN 7 q Pertemuan 12 : Penyederhanaan CFG

Penyederhanaan CFG Tujuannya : Untuk melakukan pembatasan sehingga tidak menghasilkan pohon penurunan yg memiliki kerumitan yg tdk perlu / aturan produksi yg tdk berarti.

Contoh : S→ AB | a A→a Disederhanakan menjadi : Aturan S→ AB tidak berarti karena B tidak memiliki penurunan

Contoh S→A A→B B→C C→D D→a|A Memiliki kelemahan yaitu terlalu panjang jumlahnya padahal berujung pd S → a, D → A juga menyebabkan kerumitan.

Penyederhanaan CFG Suatu tata bahasa bebas konteks (CFG) dapat disederhanakan dengan melakukan : 1. Penghilangan produksi useless 2. Penghilangan produksi unit 3. Penghilangan produksi ε

Penghilangan Produksi Useless : q Produksi yang memuat simbol variabel yang tidak memiliki penurunan yang akan menghasilkan terminal-terminal seluruhnya, produksi ini tidak berguna karena bila diturunkan tidak akan pernah selesai (masih ada simbol variabel yang tersisa) q Produksi yang tidak akan pernah dicapai dengan penurunan apapun dari simbol awal, sehingga produksi itu redundan (berlebih)

Contoh 1 : S → a. Sa | Abd | Bde A → Ada B → BBB | a Ø Simbol A tdk memiliki penurunan yg menuju terminal, sehingga bisa dihilangkan Ø Konsekuensi no 1, aturan produksi S → Abd tidak memiliki penurunan Bentuk sederhana : S → a. Sa | Bde B → BBB | a

Prinsipnya setiap kali melakukan penyederhanan kita periksa lagi aturan produksi yang tersisa, apakah semua produksi yang useless sudah dihilangkan.

Contoh 2 : S → a. B Sehingga menjadi : A → bc. D | d. AC S → a. B B → e | Ab B→e C → b. Cb | ad. F | ab C → b. Cb | ab F → c. FB Langkah penyederhaan : 1. A → b. CD, D tdk memiliki penurunan 2. Konsekuensi no 1, A tidak memiliki penurunan yang menuju terminal 3. B → Ab tidak memiliki penurunan 4. F tidak memiliki penurunan yang menuju terminal 5. C → ad. F tidak memiliki penurunan

Penghilangan Produksi ℰ adalah produksi dalam bentuk �� atau bisa dianggap sebagai produksi kosong. Penghilangan produksi �� dilakukan dengan penggantian produksi yang memuat variabel yang bisa menuju produksi �� atau biasa disebut nullable.

Contoh : S bc. Ad A �� Pada kasus diatas A nullable, maka variabel A bisa ditiadakan. Hasil penyederhanaan S bcd
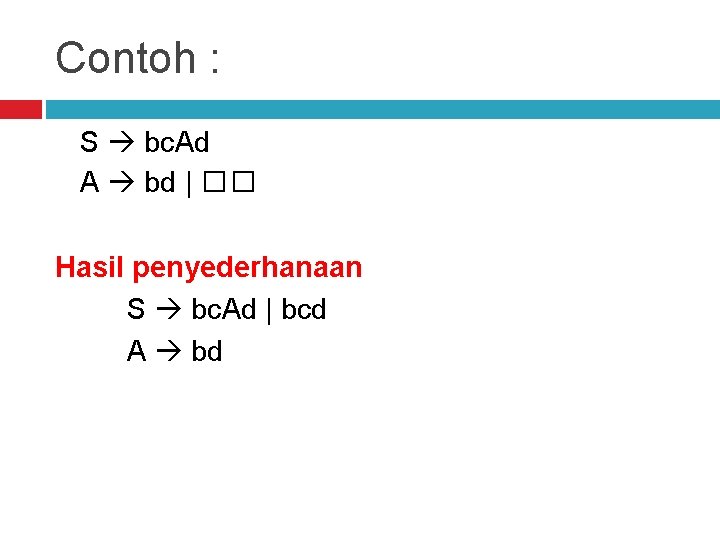
Contoh : S bc. Ad A bd | �� Hasil penyederhanaan S bc. Ad | bcd A bd
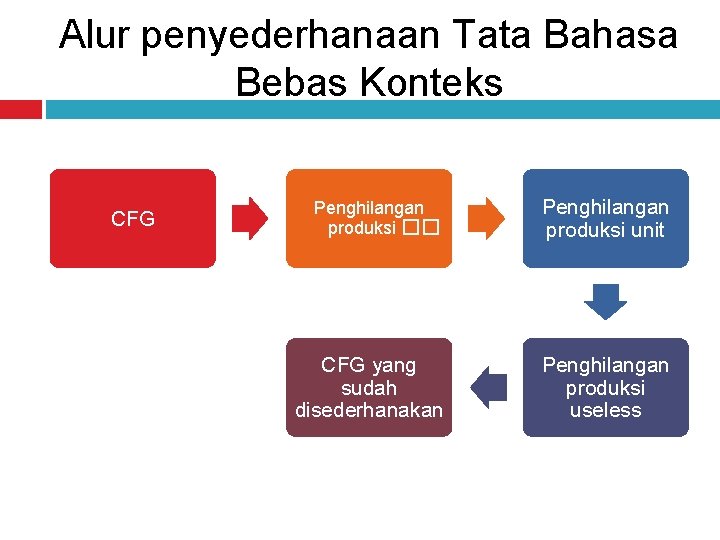
Alur penyederhanaan Tata Bahasa Bebas Konteks CFG Penghilangan produksi �� Penghilangan produksi unit CFG yang sudah disederhanakan Penghilangan produksi useless
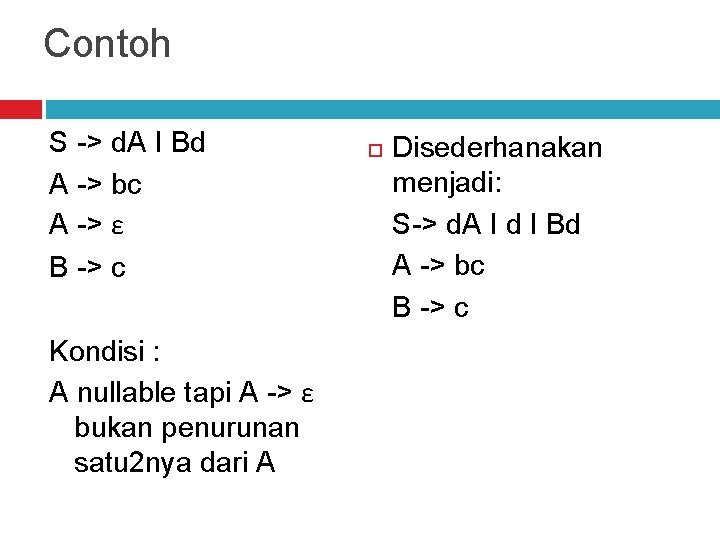
Contoh S -> d. A I Bd A -> bc A -> ε B -> c Kondisi : A nullable tapi A -> ε bukan penurunan satu 2 nya dari A Disederhanakan menjadi: S-> d. A I d I Bd A -> bc B -> c
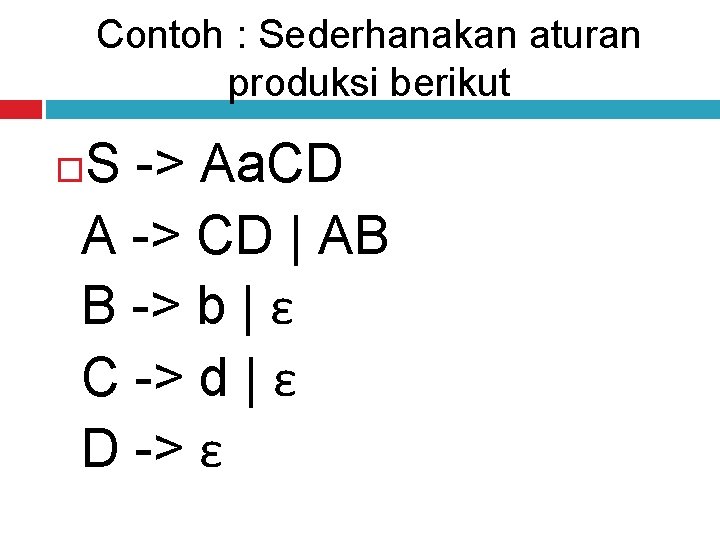
Contoh : Sederhanakan aturan produksi berikut S -> Aa. CD A -> CD | AB B -> b | ε C -> d | ε D -> ε
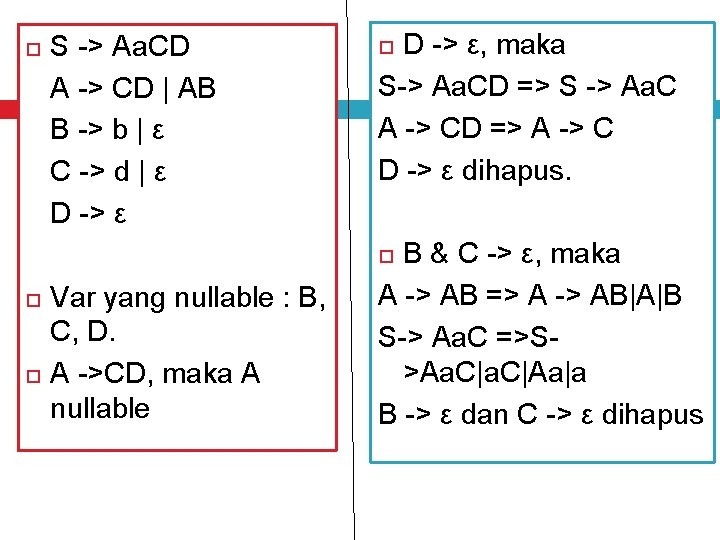
S -> Aa. CD A -> CD | AB B -> b | ε C -> d | ε D -> ε, maka S-> Aa. CD => S -> Aa. C A -> CD => A -> C D -> ε dihapus. B & C -> ε, maka A -> AB => A -> AB|A|B S-> Aa. C =>S>Aa. C|Aa|a B -> ε dan C -> ε dihapus Var yang nullable : B, C, D. A ->CD, maka A nullable

Contoh : Penyederhanaan CFG Setelah Penyederhanaan : S -> Aac|a. C|Aa|a A-> C|AB|A|B B -> b C -> d

NEXT : MESIN TURING - 28 Juli : Mesin Turing - 28 Juli : Kuis 2 - 2 Agustus: UAS
- Slides: 40