SEMESTER PENDEK 20152016 OTOMATA DAN TEORI BAHASA FORMAL

SEMESTER PENDEK 2015/2016 OTOMATA DAN TEORI BAHASA FORMAL Betha Nurina Sari, M. Kom

PERTEMUAN 3 Finite State Automata

Definisi Finite State Automata (1) Bukanlah mesin fisik tetapi suatu model matematika dari suatu sistem yang menerima input dan output diskrit. Finite State Automata memiliki state yang banyaknya berhingga dan dapat berpindah dari suatu state ke state lain. Jenis automata ini tidak memiliki tempat penyimpanan sehingga kemampuan ‘mengingatnya’ terbatas

Definisi Finite State Automata (2) Finite Automata sangat cocok untuk memodelkan sistem dengan jumlah state yang berhingga. Contoh : � Sistem elevator � Mesin untuk pengeluaran minuman kaleng ( Vending Machine) � Pengaturan lampu lalu lintas ( traffic light regulator) � Sirkuit Switching di Komputer � Neuron Nets

Finite State Automata Secara formal Finite State Automata dinyatakan oleh 5 tupel atau M=(Q, ∑, δ, S, F), dimana: Q = Himpunan state/kedudukan. ∑ = Himpunan simbol input/masukan. δ = Fungsi transisi. S = State awal/kedudukan awal (initial state), S ϵ Q. F = Himpunan state akhir ( jumlah state akhir bisa lebih dari satu)

Klasifikasi Finite Automata Finite automata dapat berupa �Deterministic Finite Automata (DFA) Dari suatu state ada tepat satu state berikutnya untuk setiap simbol input yang diterima. �Nondeterministic Finite Automata (NDFA) Dari suatu state bisa terdapat 0, 1 atau lebih busur keluar (transisi) berlabel simbol input yang sama.

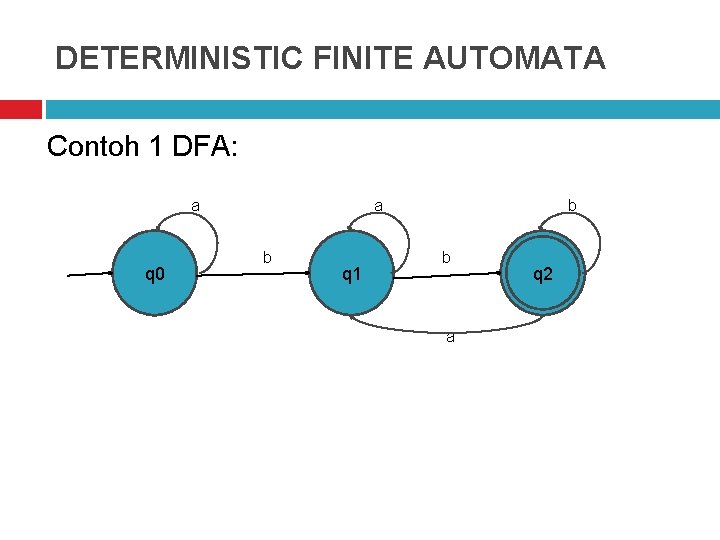
DETERMINISTIC FINITE AUTOMATA Contoh 1 DFA: a q 0 a b q 1 b b a q 2

Contoh 1 DFA Konfigurasi secara formal dinyatakan : Q = {q 0, q 1, q 2} ∑ = {a, b} S = q 0 F = {q 2} Fungsi transisi yang ada sebagai berikut : d(q 0, a)=q 0 d(q 0, b)=q 1 d(q 1, a)=q 1 d(q 1, b)=q 2 d(q 2, a)=q 1 d(q 2, b)=q 2

Contoh 1 DFA Tabel transisi tersebut menunjukan state-state berikutnya untuk kombinasi state-state dan input. Tabel transisi sbb: δ a b q 0 q 1 q 1 q 2 Latihan : Cek Input untai ‘abb’ dan ‘baba’

String yang dikenali oleh FSA merupakan suatu BAHASA yang dikenali oleh FSA tersebut. Jika dimiliki FSA M maka bahasa yang dikenali oleh FSA di notasikan sebagai : L(M) = { x | x semua string yang mengantar M dari S 0 ke (Si ϵ Z) } Untuk mesin FSA pada contoh 1 DFA : L(M) = {bb, abab, ababb, anbanbbna, …}

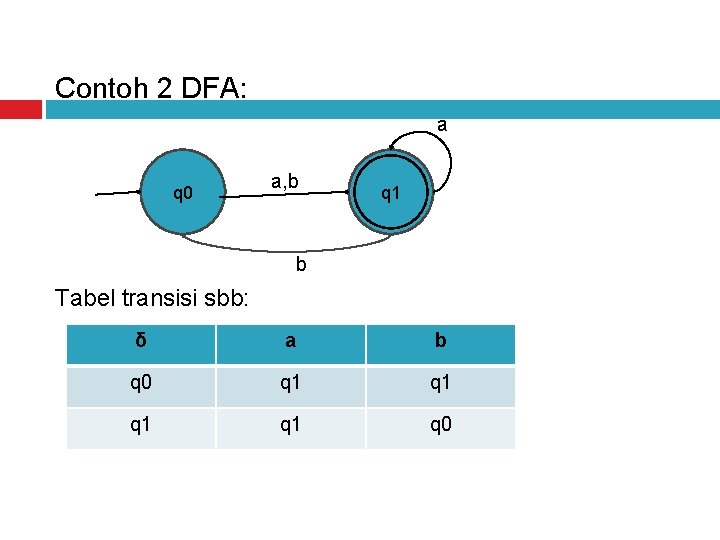
Contoh 2 DFA: a q 0 a, b q 1 b Tabel transisi sbb: δ a b q 0 q 1 q 1 q 0

Non-Deterministic Finite Automata (NFA) Pada NFA dari suatu state bisa terdapat 0, 1 atau lebih busur keluar (transisi) berlabel simbol yang sama. Disini perbedaan ada pada fungsi transisinya, dimana untuk setiap pasangan state-input, kita bisa memiliki 0 atau lebih pilihan untuk state berikutnya.

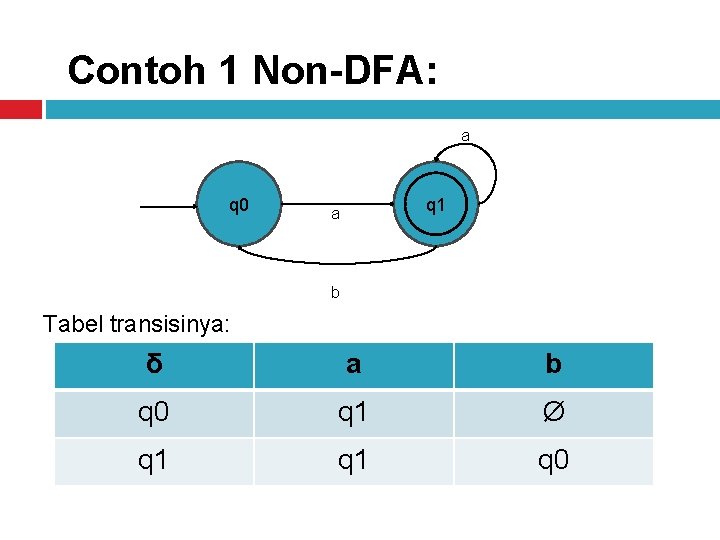
Contoh 1 Non-DFA: a q 0 q 1 q 0 a b Tabel transisinya: δ a b q 0 q 1 Ø q 1 q 0

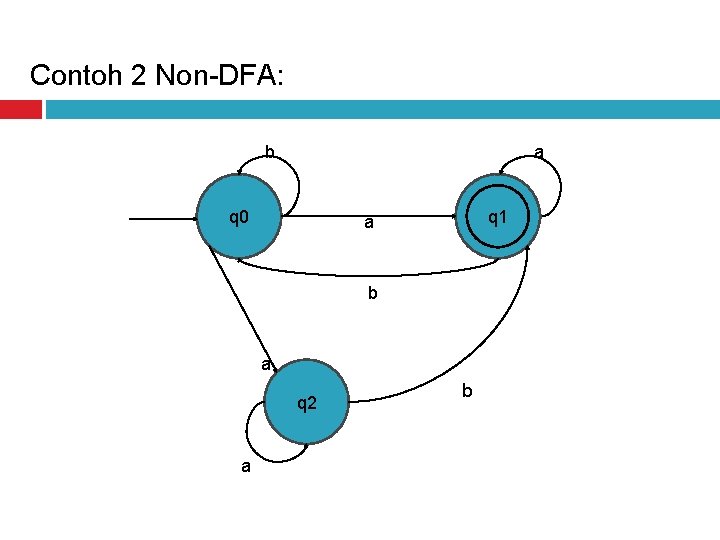
Contoh 2 Non-DFA: b a q 0 q 1 q 0 a b a q 2 a b

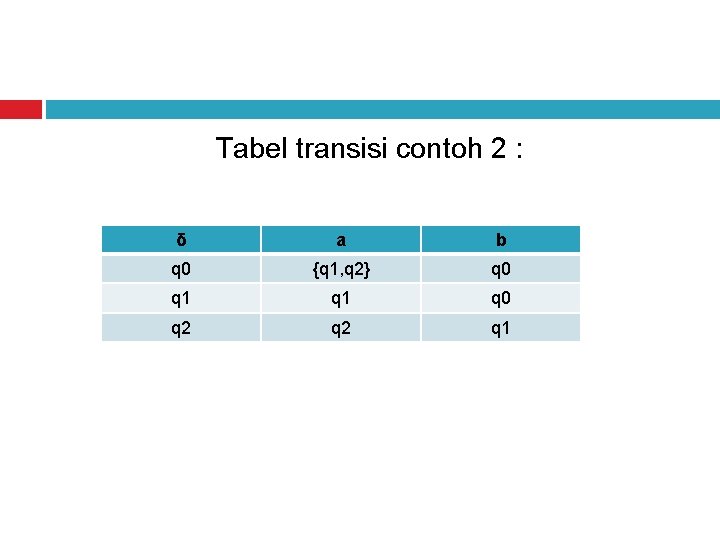
Tabel transisi contoh 2 : δ a b q 0 {q 1, q 2} q 0 q 1 q 0 q 2 q 1

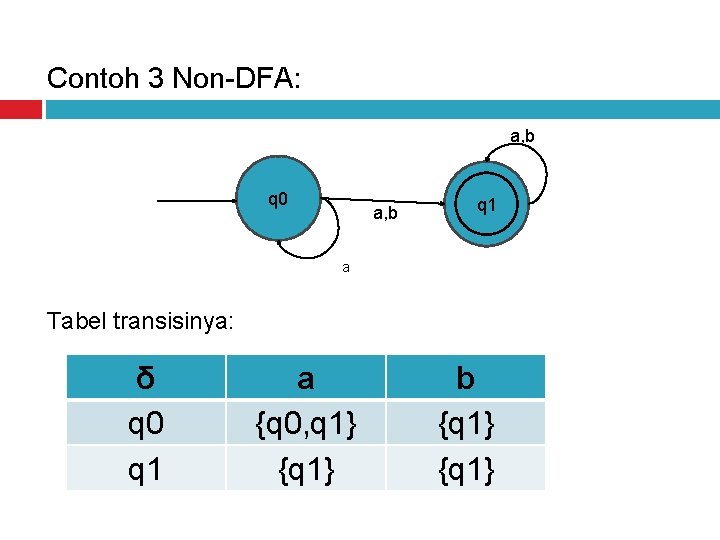
Contoh 3 Non-DFA: a, b q 0 a, b q 1 q 0 a Tabel transisinya: δ q 0 q 1 a {q 0, q 1} {q 1} b {q 1}

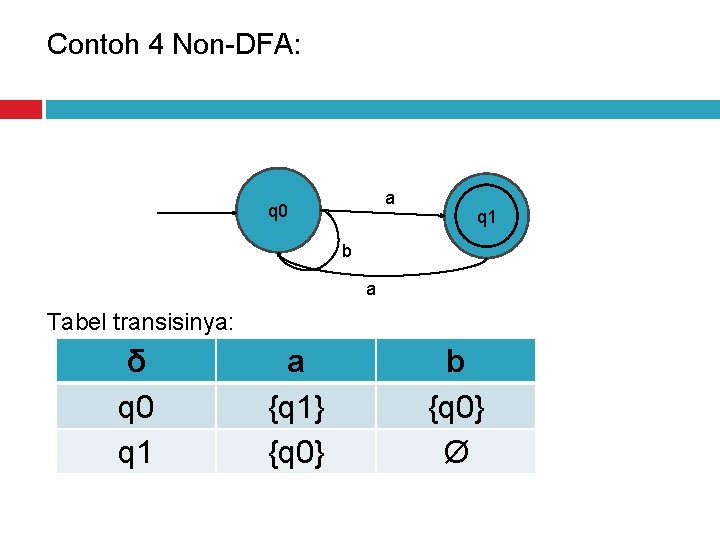
Contoh 4 Non-DFA: a q 0 q 1 q 0 b a Tabel transisinya: δ q 0 q 1 a {q 1} {q 0} b {q 0} Ø

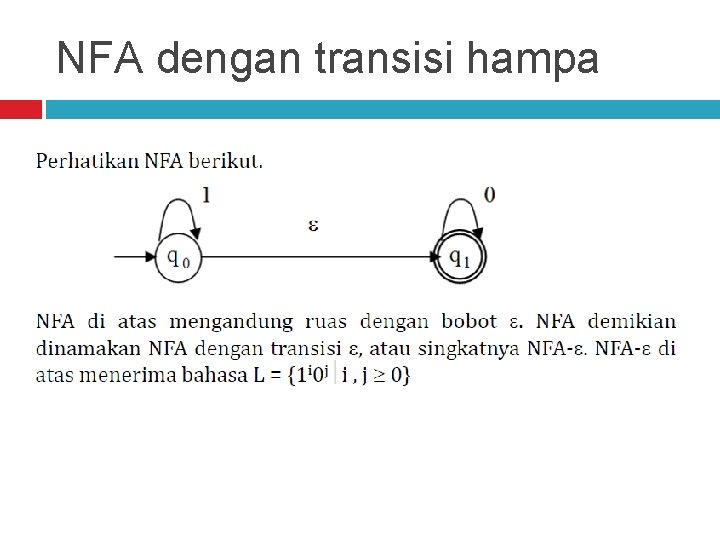
NFA dengan transisi hampa

Ekuivalensi Antar Deterministic Finite Automata Dua Deterministic Finite Automata dikatakan ekuivalen jika L(M 1) = L(M 2). Dimana : �M = deterministic Finite Automata �L(M) = bahasa

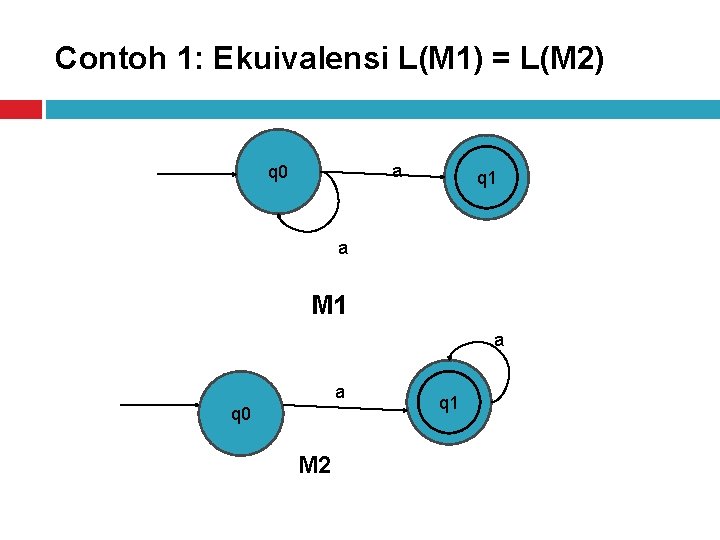
Contoh 1: Ekuivalensi L(M 1) = L(M 2) a q 0 q 1 q 0 a M 1 a a q 0 M 2 q 1 q 0

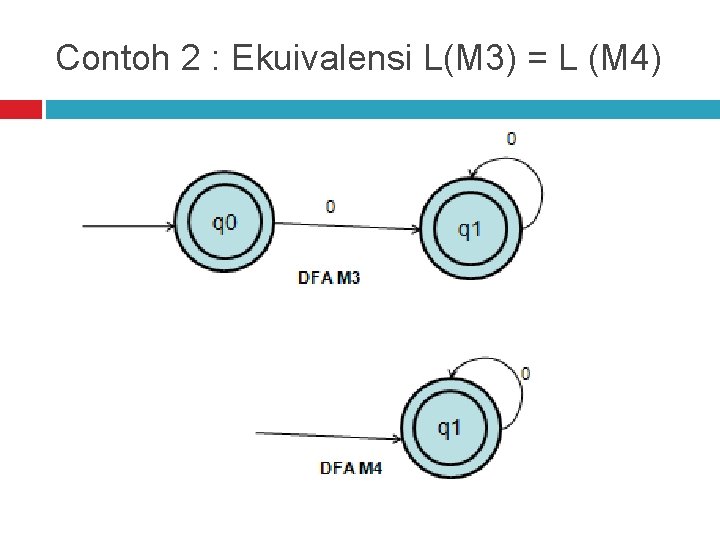
Contoh 2 : Ekuivalensi L(M 3) = L (M 4)

NEXT >>> QUIZ Online Materi 1 -3