Otomata Teori Bahasa Pertemuan 1 Firrar Utdirartatmo Teori

Otomata & Teori Bahasa Pertemuan 1 Firrar Utdirartatmo: Teori Bahasa dan Otomata JJ Learning Yogyakarta, Fasilkom-Udinus

Introduction Ø Nurul Anisa Sri Winarsih, M. Cs Ø Teknik Informatika – S 1 (Lab D. 2. F) Ø 0812 2543 1994 Ø Bidang Kajian: Software Engineering and Intelligence Ø Email : nurulanisasw@dsn. dinus. ac. id Fasilkom-Udinus

Komponen Penilaian Ø Tugas+Responsi : 40% Ø Ujian Tengah Semester : 30% Ø Ujian Akhir Semster : 30% Ø Peraturan: üIjin menggunakan surat üDilarang mempresensikan ü Keterlambatan max 30 menit üKalau Fasilkom-Udinus

Deskripsi Otomata dan Teori Bahasa Ø Otamata dan Teori Bahasa (OTB) matakuliah wajib Ø Komponen utama dari Ilmu Komputer yaitu model dan gagasan mendasar mengenai komputasi. suatu bentuk yang memiliki fungsi-fungsi dari komputer digital, menerima input, menghasilkan output, bisa memiliki penyimpanan sementara, dan mampu membuat keputusan dalam menstransformasikan dari input ke output Fasilkom-Udinus

Outcome Pembelajaran Ø Setelah memenuhi tujuan pembelajaran mata kuliah ini mahasiswa diharapkan : Ø Mampu memahami pengertian dari otomata dan teori bahasa. Ø Mampu menerapkan otomata dan teori bahasa dalam kehidupan sehari -hari Fasilkom-Udinus

Referensi Ø Firrar Utdirartatmo, Teori Bahasa dan Otomata, JJ Learning Yogyakarta, 2001 Ø Bambang Hariyanto, Teori Bahasa, Otomata, dan Komputasi serta Terapannya, Informatika Bandung, 2004 Ø Dean Kelley, Otomata dan Bahasa-bahasa Formal, PT. Prenhallindo, Jakarta, 1999 Fasilkom-Udinus

Contents 1 2 3 4 • Definisi dan pengertian • Kedudukan OTB • Tata Bahasa • Klasifikasi Tata Bahasa Fasilkom-Udinus

1. Otomata & Teori Bahasa? Ø Bagian dari teori komputasi pada ilmu komputer Ø Otomata adalah model matematika yang memiliki fungsi dari komputer digital yaitu menerima input, menghasilkan output, bisa memiliki penyimpanan sementara dan mampu membuat keputusan dalam transformasi input ke output Ø Penekanannya adalah pada pemecahan masalah ØMisal, Penggunaan lift. Kita dari lantai 1 mau naik ke lantai 5. Lalu ada orang yang menekan tombol lift dari lantai 3. Bagaimana? ØMaka dari itu, sebelum membuat program untuk lift, maka kita harus memodelkannya terlebih dahulu. Fasilkom-Udinus

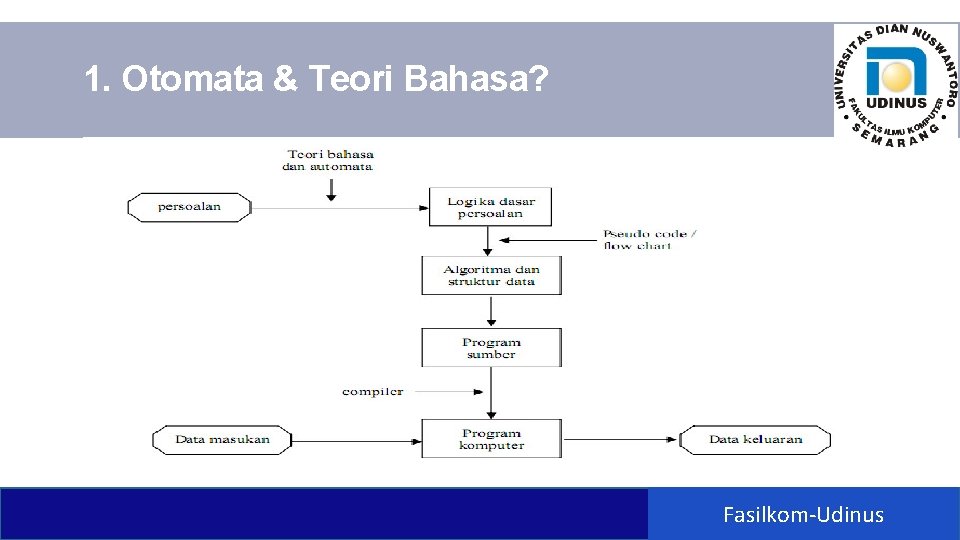
1. Otomata & Teori Bahasa? Fasilkom-Udinus

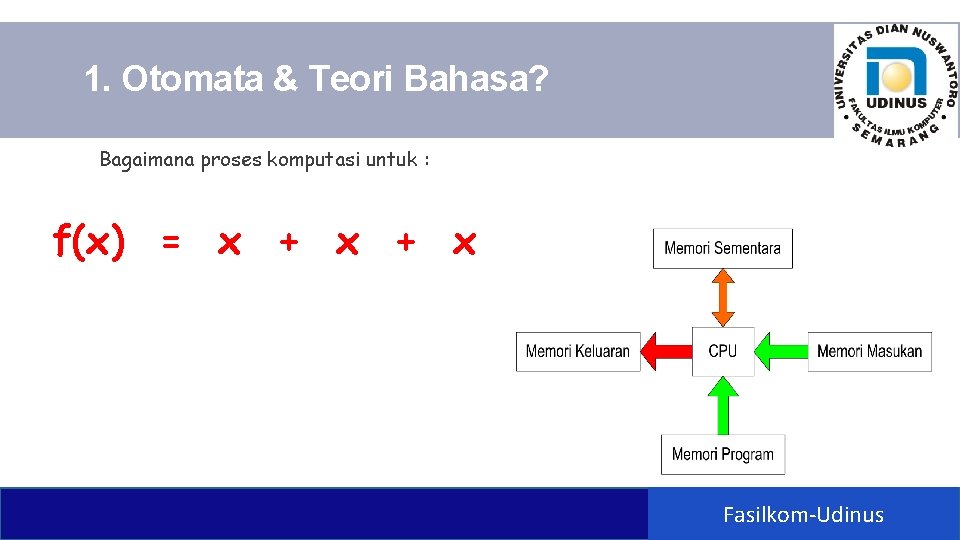
1. Otomata & Teori Bahasa? Bagaimana proses komputasi untuk : f(x) = x + x Fasilkom-Udinus

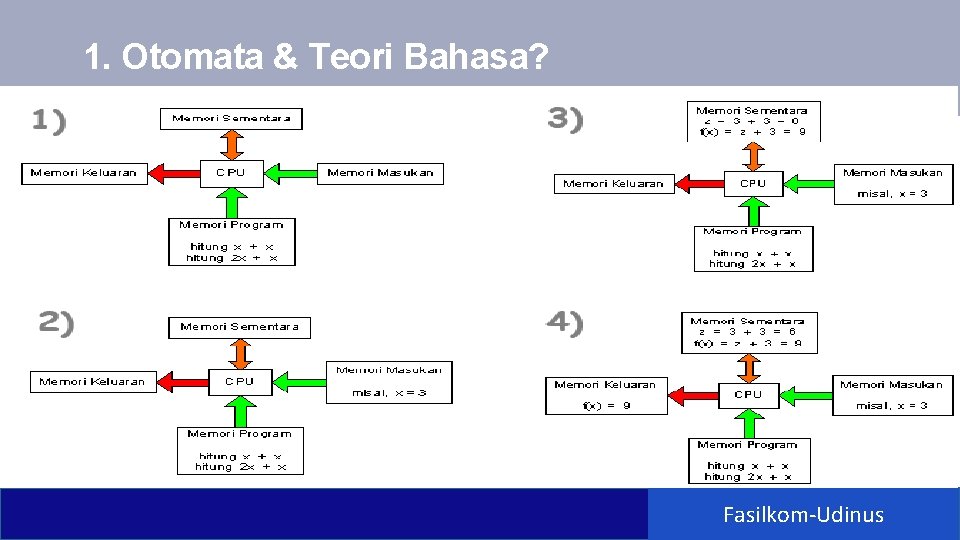
1. Otomata & Teori Bahasa? Fasilkom-Udinus

2. Kedudukan OTB Sub bidang apapun dalam ilmu informatika pasti memiliki 2 komponen : 1. Ide/gagasan di representasikan dalam bentuk Model komputasi beberapa disiplin ilmu yang dapat di adaptasi: § Neuro Nets Finite Automata § Sistem Logika Formal Proof method § Sistem Tata Bahasa Psycho-Linguistic 2. Teknik rekayasa untuk perancangan sistem komputasi, meliputi perangkat keras, perangkat lunak, khususnya penerapan rancangan dari teori. Otomata dan Teori Bahasa merupakan bagian pertama Fasilkom-Udinus

3. Tata Bahasa Ø Penulisan suatu kalimat dalam sebuah bahasa, akan mengikuti suatu aturan tertentu yang berlaku pada bahasa tersebut. Ø Aturan tersebut dikenal sebagai Tata Bahasa (Grammar). Fasilkom-Udinus

3. Tata Bahasa Fasilkom-Udinus

3. Tata Bahasa 1. Adik menulis 2. Kucing menggigit tikus 3. Si kambing cantik memakan sayuran segar Periksalah kalimat berikut apakah memenuhi aturan tersebut : 1. Si tikus jorok mengejar kucing galak 2. Si bola besar menendang kambing jelek Fasilkom-Udinus

3. Tata Bahasa Ø Tata bahasa (grammar): kumpulan dari himpunan-himpunan variabel, simbol-simbol terminal, simbol awal yang dibatasi oleh aturan-aturan produksi. Ø Pada tahun 1959 seorang ahli bernama Noam Chomsky membuat model matematis untuk mendeskripsikan Bahasa sekaligus menjawab pertanyaan ttg psycho-linguistic dan membuat perangkat formal untuk memodelkan Bahasa (disebut Grammar) Fasilkom-Udinus

3. Tata Bahasa Fasilkom-Udinus

3. Tata Bahasa Fasilkom-Udinus

4. Klasifikasi Tata Bahasa Fasilkom-Udinus

Konsep Bahasa Ø Abjad Ø String Ø Bahasa (Language) Ø Bahasa Kosong Ø Bahasa Universal dari ∑ Fasilkom-Udinus

Konsep Bahasa Ø Abjad § Sebuah himpunan berhingga tak kosong dari simbol – simbol. § Notasi : ∑ § ∑ = {a, b, c, . . . , x, y, z} (Roman alphabet) § ∑ = {0, 1, . . . , 9} § ∑ = {0, 1} (binary alphabet) Fasilkom-Udinus

Konsep Bahasa Ø Bahasa (Language) n Kumpulan dari string. Notasi : L ∑ = {1, 2, 3, 4, 5}, ini abjad o Kumpulan {1, 123, 12345, 112} adalah bahasa dari abjad tersebut o ∑ = {1}, ini abjad o Kumpulan {1, 111, 1111, …} adalah sebuah Bahasa. o Ø Bahasa Kosong n Suatu bahasa yang tidak terdiri dari string. Notasi : {} atau Ø Fasilkom-Udinus

Konsep Bahasa Ø Bahasa universal dari ∑ Bahasa yang terdiri dari semua string berdasarkan suatu abjad ∑ n Notasi ∑* n ∑ = {1}, maka ∑* = {ɛ, 1, 111, 1111, …} n Fasilkom-Udinus

Aturan Produksi Aturan produksi α→β yang diterapkan pada suatu string w=aαc mengganti kemunculan. α menjadi β, sehingga string tersebut berubah menjadi w=aβc, sehingga dapat dituliskan aαc ⇒aβc (aαc memproduksi aβc). ØProduksi tersebut dapat diterapkan berkali-kali w 1 ⇒w 2 ⇒w 3 ⇒. . . ⇒wn Øatau dapat dituliskan w 1 ⇒*wn Øjika minimal harus ada 1 aturan produksi yang diterapkan : w 1 ⇒+wn Fasilkom-Udinus

Aturan Produksi S start state P aturan produksi Symbol non terminal di kanan Simbol terminal di kiri L language, G grammar Kalau di OTB, 7 pangkat 0 = 0 Fasilkom-Udinus

Aturan Produksi Tata bahasa G = {{S, A} , {a, b}, S , P } dengan aturan produksi P adalah S →Ab A →a. Ab A→ε tuliskan string apa yang di hasilkan pada aturan produksi di atas! Fasilkom-Udinus

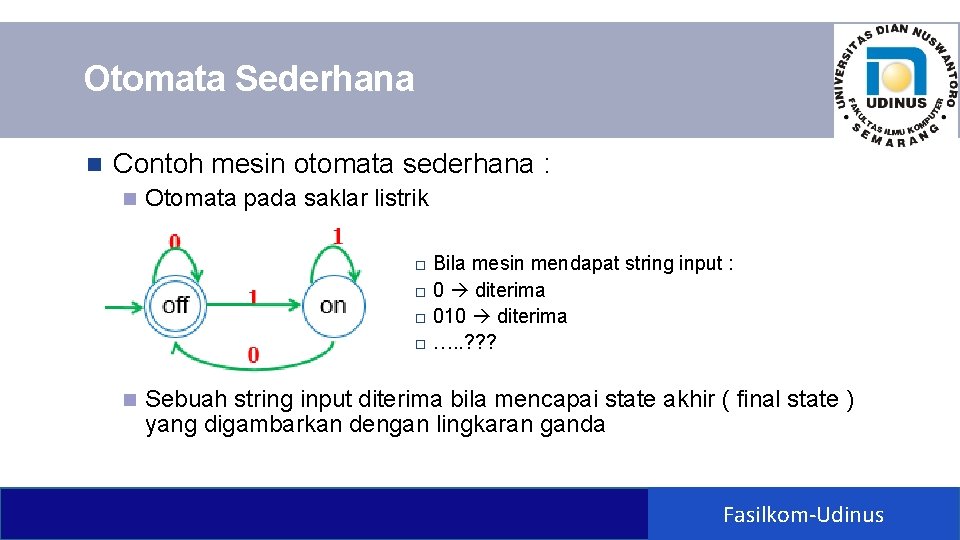
Otomata Sederhana n Contoh mesin otomata sederhana : n Otomata pada saklar listrik Bila mesin mendapat string input : o 0 diterima o 010 diterima o …. . ? ? ? o n Sebuah string input diterima bila mencapai state akhir ( final state ) yang digambarkan dengan lingkaran ganda Fasilkom-Udinus

Otomata Sederhana n Finite automaton berikut dapat dinyatakan sebagai bagian dari lexical analyzer. Fasilkom-Udinus