Optimisation non linaire sans contraintes Recherche oprationnelle GCSIE

Optimisation non linéaire sans contraintes Recherche opérationnelle GC-SIE Méthodes de descente Michel Bierlaire

Méthodes de descente Michel Bierlaire

Directions de descente § Problème : § min f : IRn IR f continûment différentiable Idée : – – On démarre d’un point x 0 On génére des vecteurs x 1, x 2, … tels que la valeur de f décroit à chaque itération : f(xk+1) < f(xk) k=1, 2, … Méthodes de descente Michel Bierlaire 3

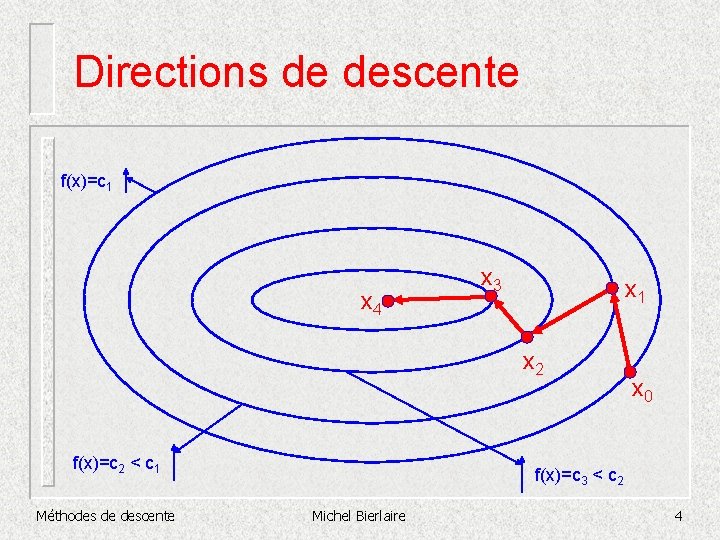
Directions de descente f(x)=c 1 x 4 x 3 x 1 x 2 f(x)=c 2 < c 1 Méthodes de descente x 0 f(x)=c 3 < c 2 Michel Bierlaire 4

Directions de descente § § § Soit x IRn tel que f(x) 0. Condidérons la demi-droite xa = x – a f(x) Théorème de Taylor (1 er ordre) f(x+s) = f(x) + f(x)Ts + o(¦¦s¦¦) avec s = xa-x f(xa) = f(x) + f(x)T(xa-x) + o(¦¦xa-x¦¦) = f(x) – a ¦¦ f(x)¦¦ 2 + o(a¦¦ f(x)¦¦) = f(x) – a ¦¦ f(x)¦¦ 2 + o(a) Méthodes de descente Michel Bierlaire 5

Directions de descente f(xa) = f(x) – a ¦¦ f(x)¦¦ 2 + o(a) § Si a est petit, on peut négliger o(a) § Donc, pour a positif mais petit, f(xa) < f(x) Théorème : § Il existe d tel que, pour tout a ]0, d[ f(x- a f(x)) < f(x) Méthodes de descente Michel Bierlaire 6

Directions de descente § § § Gradient = plus forte pente Question : y a-t-il d’autres directions de descente que - f(x) ? Appliquons le même raisonnement avec d 0. Méthodes de descente Michel Bierlaire 7

Directions de descente § § Condidérons la demi-droite xa = x + a d Théorème de Taylor (1 er ordre) f(x+s) = f(x) + f(x)Ts + o(¦¦s¦¦) avec s = xa-x f(xa) = f(x) + f(x)T(xa-x) + o(¦¦xa-x¦¦) = f(x) + a f(x)Td + o(a ¦¦d¦¦) = f(x) + a f(x)Td + o(a) Méthodes de descente Michel Bierlaire 8

Directions de descente f(xa) = f(x) + a f(x)Td + o(a) § Si a est petit, on peut négliger o(a) § Pour avoir f(xa) < f(x), il faut f(x)Td < 0 Théorème : § Soit d tel que f(x)Td < 0. Il existe d tel que, pour tout a ]0, d[ f(x+ad) < f(x) Méthodes de descente Michel Bierlaire 9

Directions de descente Définition : § Soit f: IRn IR, une fonction continûment différentiable, et x un vecteur de IRn. Le vecteur d IRn est appelé direction de descente de f en x ssi f(x)Td < 0 Méthodes de descente Michel Bierlaire 10

Méthodes de descente Algorithme de base : § Soit x 0 IRn. Poser k=0. § Tant que f(xk) 0 – – – Choisir dk tel que f(xk)Tdk < 0 Choisir ak > 0 Poser xk+1 = xk + ak dk Méthodes de descente Michel Bierlaire 11

Méthodes de descente Notes : § Il y a beaucoup de choix possibles § En général, on choisit ak tel que f(xk+akdk) < f(xk) mais il y a des exceptions § Il n’y a aucune garantie de convergence pour l’algorithme de base Méthodes de descente Michel Bierlaire 12

Choix de la direction § § Ecrivons dk = -Dk f(xk) où Dk est une matrice n x n La condition f(xk)Tdk < 0 s’écrit f(xk)T Dk f(xk) > 0 Si Dk est définie positive, cette condition est toujours vérifiée. Le choix de la direction revient donc au choix d’une matrice définie positive. Méthodes de descente Michel Bierlaire 13

Choix de la direction Quelques exemples souvent utilisés § Méthode de la plus forte pente – – § Dk = I xk+1 = xk – ak f(xk) Méthode de Newton – – Dk = ( 2 f(xk))-1 xk+1 = xk – ak ( 2 f(xk))-1 f(xk) Méthodes de descente Michel Bierlaire Attention: il faut que 2 f(xk) soit inversible et déf. pos. 14

Choix de la direction § Mise à l’échelle diagonale - Dk = - dki > 0 pour tout i - Exemple : dki = Méthodes de descente Michel Bierlaire 15

Choix de la direction § Méthode de Newton modifiée – – § Dk = ( 2 f(x 0))-1 xk+1 = xk – ak ( 2 f(x 0))-1 f(xk) etc… Méthodes de descente Michel Bierlaire 16

Choix du pas Règle de minimisation 1. § Problème à une seule variable Règle d’approximation 2. § § Minimisation prend du temps Section d’or nécessite l’unimodalité A-t-on besoin du minimum exact ? Idée : § Méthodes de descente Choisir un pas qui diminue suffisamment la valeur de la fonction. Michel Bierlaire 17

Choix du pas : approximation § Démarche: – – § Voyons d’abord ce que sont de « mauvais » pas. Déterminons des règles empêchant les « mauvais » pas. Prenons – – f(x) = x 2 x*= 0 Méthodes de descente Michel Bierlaire 18

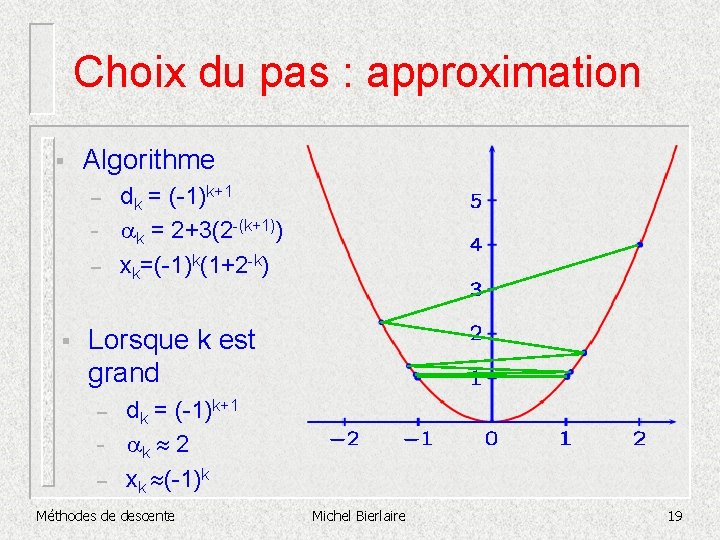
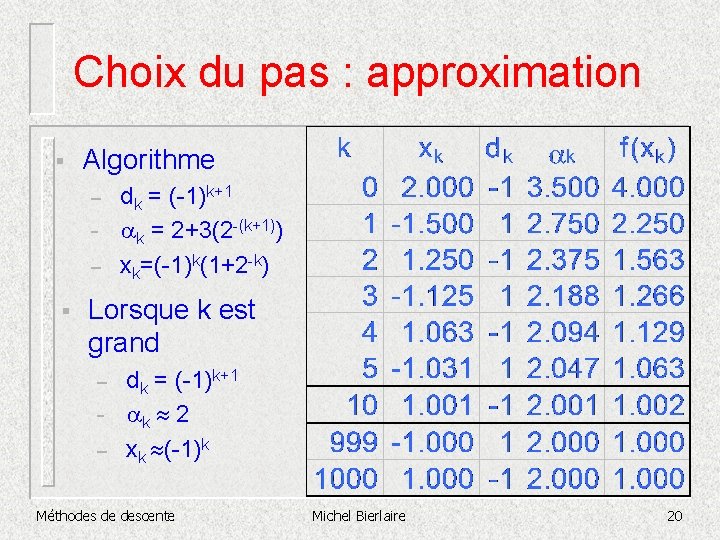
Choix du pas : approximation § Algorithme – – – § dk = (-1)k+1 ak = 2+3(2 -(k+1)) xk=(-1)k(1+2 -k) Lorsque k est grand – – – dk = (-1)k+1 ak 2 xk (-1)k Méthodes de descente Michel Bierlaire 19

Choix du pas : approximation § Algorithme – – – § dk = (-1)k+1 ak = 2+3(2 -(k+1)) xk=(-1)k(1+2 -k) Lorsque k est grand – – – dk = (-1)k+1 ak 2 xk (-1)k Méthodes de descente Michel Bierlaire 20

Choix du pas : approximation § Problème : – § très petites diminutions de f relativement à la longueur des pas Solution : – exiger une diminution suffisante de f Méthodes de descente Michel Bierlaire 21

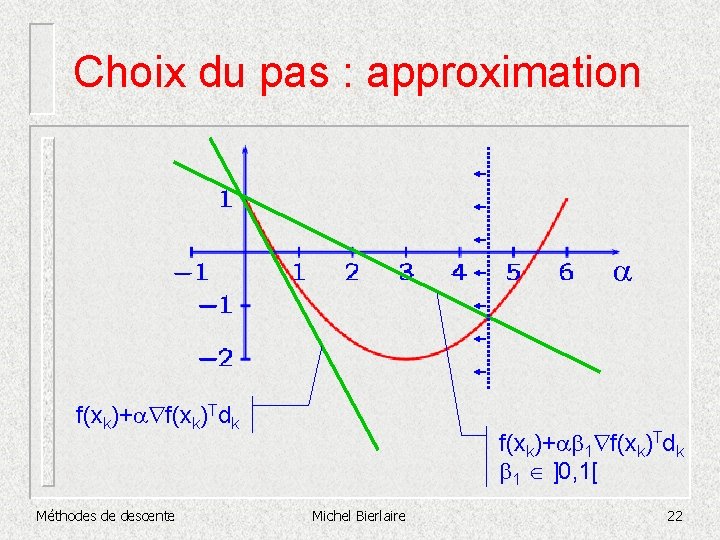
Choix du pas : approximation a f(xk)+a f(xk)Tdk Méthodes de descente f(xk)+ab 1 f(xk)Tdk b 1 ]0, 1[ Michel Bierlaire 22

Choix du pas : approximation § On choisit ak tel que f(xk+akdk) £ f(xk)+akb 1 f(xk)Tdk b 1 ]0, 1[ § § Reprenons l’exemple (k grand et impair) f(x)=x 2, xk = -1, dk=1, ak=2, f’(x)=2 x f(-1+2 1) £ 1+2 b 1(-2 1) 1 £ 1 – 4 b 1 £ 0 Impossible L’algorithme sera rejeté par cette règle Méthodes de descente Michel Bierlaire 23

Choix du pas : approximation § Conditions d’Armijo-Goldstein f(xk+akdk) £ f(xk)+akb 1 f(xk)Tdk b 1 ]0, 1[ Méthodes de descente Michel Bierlaire 24

Choix du pas : approximation Algorithme de recherche linéaire § Soient g(a), b 1, l ]0, 1[, a 0 > 0 § Pour k=1, 2, … – – Si f(xk+akdk) £ f(xk)+akb 1 f(xk)Tdk alors a*=ak STOP ak+1 = l ak Méthodes de descente Michel Bierlaire 25