Les algorithmes complexit et notation asymptotique 1 Analyse

Les algorithmes: complexité et notation asymptotique 1

Analyse d'algorithmes Notation O( ) Comparer deux algorithmes § Soient deux algorithmes A 1 et A 2 § Base de comparaison § Mesure indépendante de l'implémentation : TAILLE D'UN PROBLÈME (n) § Temps d'exécution d'un algorithme = fonction(taille du problème) i. e. f(n) § Exemples : § Taille d'une liste (recherche d'un élément dans une liste) § Nombre de nœuds d'un arbre (impression d'un arbre) § Taille d'un tableau (tri) 2

Analyse d'algorithmes Notation O( ) 3

Analyse d'algorithmes Notation O( ) 4

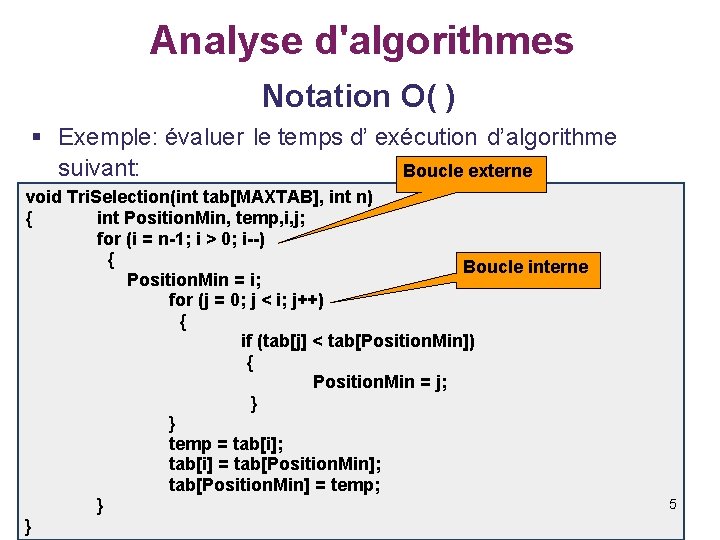
Analyse d'algorithmes Notation O( ) § Exemple: évaluer le temps d’ exécution d’algorithme suivant: Boucle externe void Tri. Selection(int tab[MAXTAB], int n) { int Position. Min, temp, i, j; for (i = n-1; i > 0; i--) { Boucle interne Position. Min = i; for (j = 0; j < i; j++) { if (tab[j] < tab[Position. Min]) { Position. Min = j; } } temp = tab[i]; tab[i] = tab[Position. Min]; tab[Position. Min] = temp; } } 5

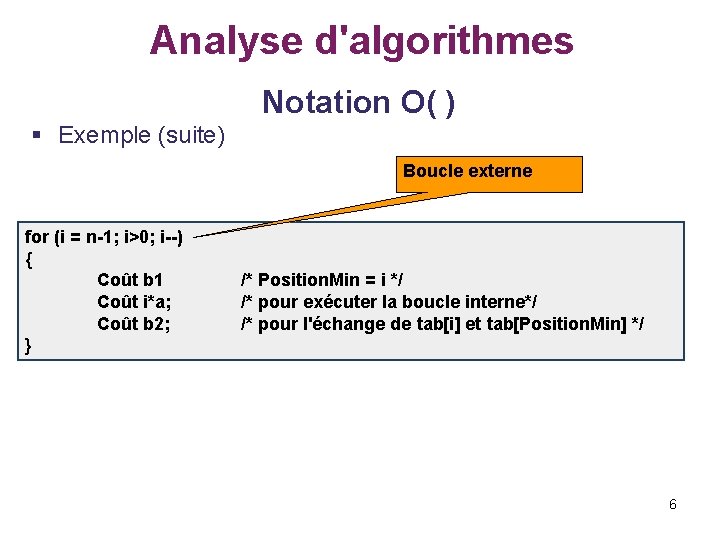
Analyse d'algorithmes Notation O( ) § Exemple (suite) Boucle externe for (i = n-1; i>0; i--) { Coût b 1 Coût i*a; Coût b 2; } /* Position. Min = i */ /* pour exécuter la boucle interne*/ /* pour l'échange de tab[i] et tab[Position. Min] */ 6

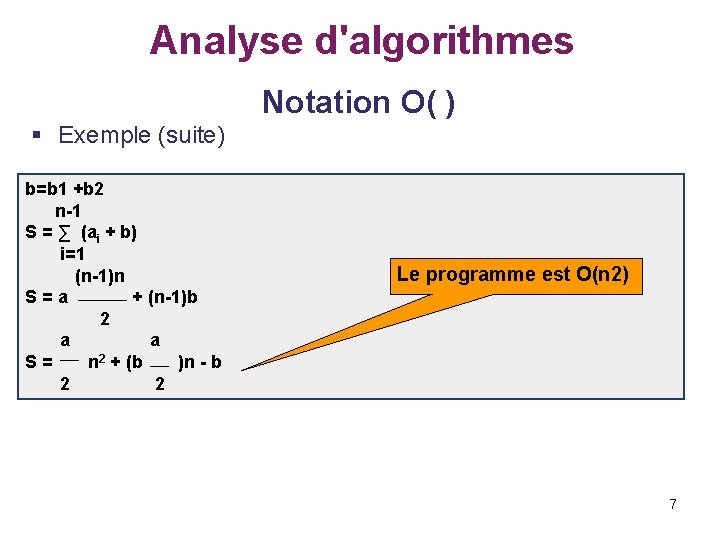
Analyse d'algorithmes Notation O( ) § Exemple (suite) b=b 1 +b 2 n-1 S = ∑ (ai + b) i=1 (n-1)n S=a + (n-1)b 2 a a S= n 2 + (b )n - b 2 2 Le programme est O(n 2) 7

Analyse d'algorithmes Notation O( ) Définition du O( ) § Nous dirons que f(n) est O(g(n)) s'il existe deux constantes positives K et n 0 tel que |f(n)| <= K |g(n)| pour tout n>n 0 § Conclusion : § Évaluer le coût d'un algorithme = Recher la fonction g(n) qui est la plus proche au dessus ou égale a f(n) 8

Analyse d'algorithmes La recherche séquentielle A. Données pas triées § § recherche(3) = 1 comparaison recherche(10) = 11 comparaisons recherche(12) = 7 comparaisons recherche(13) = 11 comparaisons § § meilleur cas = O(1) pire cas = O(n) en moyenne = O(n/2) absences = O(n) 9

Analyse d'algorithmes La recherche séquentielle B. Données triées § § recherche(1) = 1 comparaison recherche(14) = 11 comparaisons recherche(8) = 6 comparaisons recherche(13) = 11 comparaisons § § meilleur cas = O(1) pire cas = O(n) en moyenne = O(n/2) absences = O(n/2) 10

11

12

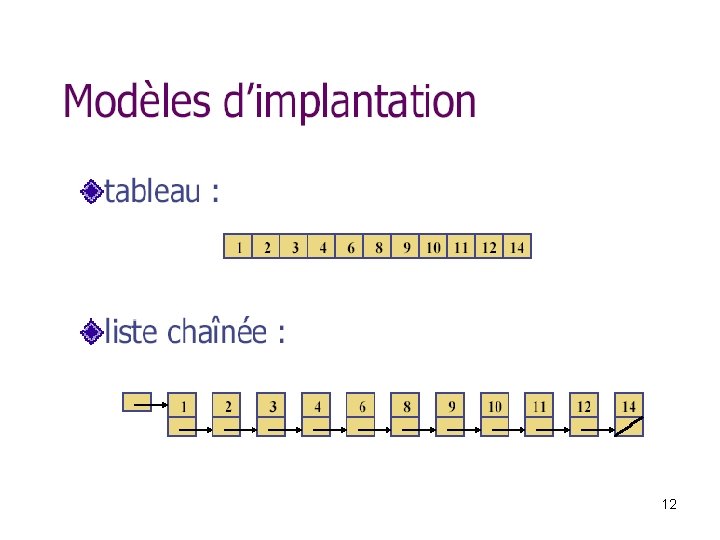
Analyse d'algorithmes La recherche binaire § implantation en tableau = accès direct à n’importe quel élément § en regardant tout de suite au milieu, on peut éliminer la moitié des données 13

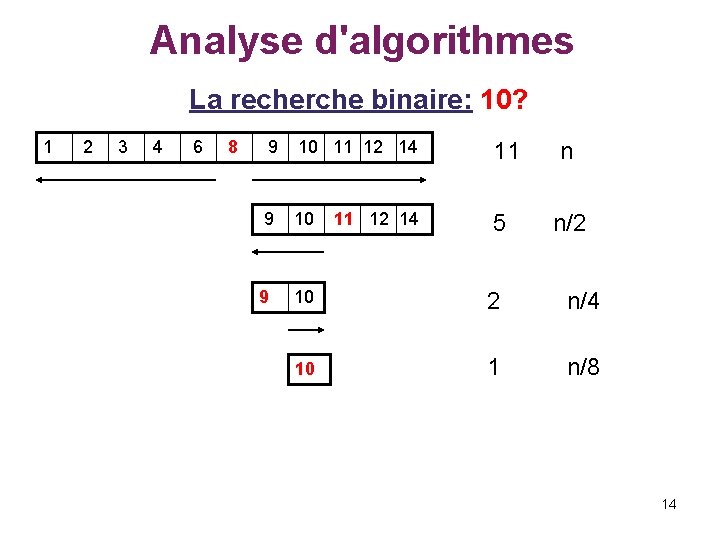
Analyse d'algorithmes La recherche binaire: 10? 1 2 3 4 6 8 9 10 11 12 14 11 n 9 10 5 n/2 9 10 2 n/4 10 1 n/8 11 12 14 14

Analyse d'algorithmes Algorithme récursif 1 § § § 2 3 4 6 8 9 10 11 12 14 récursion ? conditions d’arrêt ? convergence ? 15

Analyse d'algorithmes Algorithme récursif - récursion 1 2 § 3 4 6 8 9 10 11 12 14 X Є tab[debut. . fin] § § § si x = tab[milieu] (condition d’arrêt) si x < tab[milieu] et x Є tab[debut. . milieu-1] si x > tab[milieu] et x Є tab[milieu+1. . fin] 16

Analyse d'algorithmes Algorithme récursif - conditions d’arrêt 1 § § 2 3 4 6 8 9 10 11 12 14 X € tab[debut. . fin] si debut > fin X Є tab[debut. . fin] si x = tab[milieu] 17

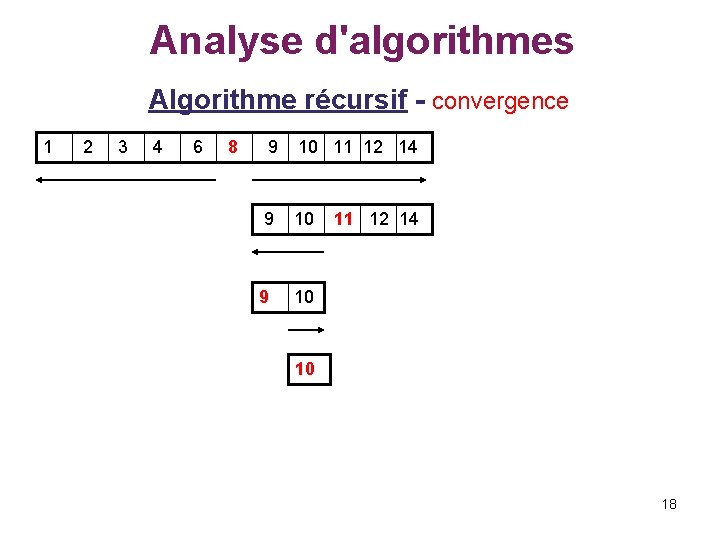
Analyse d'algorithmes Algorithme récursif - convergence 1 2 3 4 6 8 9 10 11 12 14 10 18

Analyse d'algorithmes Algorithme récursif 1 2 3 4 6 8 9 10 11 12 14 int recherche. Bin. Rec(int tab[ ], int val, int debut, int fin) { int milieu; if (debut > fin) return -1; else { milieu= (debut + fin)/2; if( val == tab[milieu]) return milieu; else { if( val < tab[milieu]) return(recherche. Bin. Rec(tab, val, debut, milieu-1)); else return(recherche. Bin. Rec(tab, val, milieu+1, fin)); } } 19 }

Analyse d'algorithmes Algorithme récursif Recherche séquentielle (données triées) § § Données présentes: O(n/2) Données absentes: O(n/2) Recherche binaire (données triées) § Données présentes: O(log n) § Données absentes: O(log n) 20

Analyse d'algorithmes Algorithme récursif § § Il vaut bien mieux implanter cet algorithme de manière itérative, car la fonction se rappelle jusqu'à trouver la position désirée, puis seulement on effectue les dépilages, alors que l'on n'a plus besoin des états intermédiaires qui ont été mémorisés par la récursivité puisque le problème est résolu. 21