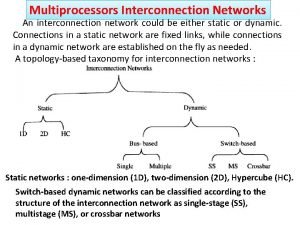
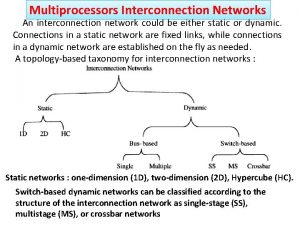
Multiprocessor Interconnection Networks Mahim Mishra CS 495 April

Multiprocessor Interconnection Networks Mahim Mishra CS 495 April 16, 2002 Topics • Network design issues • Network Topology • Performance

Networks • How do we move data between processors? • Design Options: • Topology • Routing • Physical implementation – 2– CS 495 S’ 02

Evaluation Criteria • Latency • Bisection Bandwidth • Contention and hot-spot behavior • Partitionability • Cost and scalability • Fault tolerance – 3– CS 495 S’ 02

Communication Perf: Latency Time(n)s-d = overhead + routing delay + channel occupancy + contention delay occupancy = (n + ne) / b Routing delay? Contention? – 4– CS 495 S’ 02

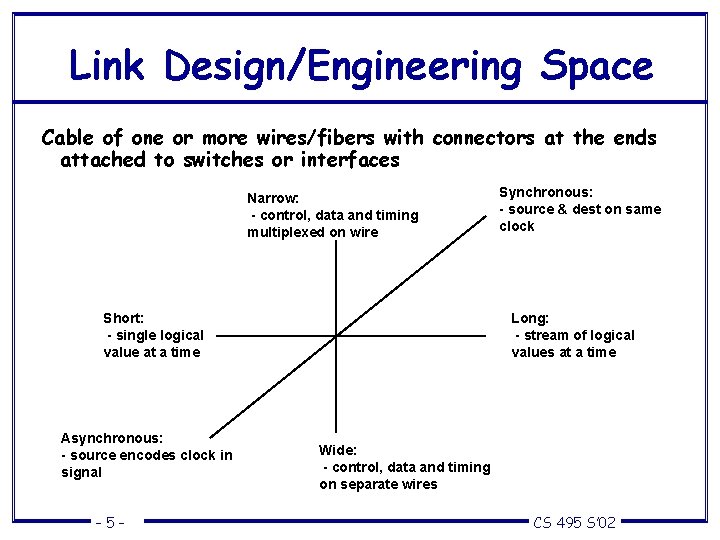
Link Design/Engineering Space Cable of one or more wires/fibers with connectors at the ends attached to switches or interfaces Narrow: - control, data and timing multiplexed on wire Short: - single logical value at a time Asynchronous: - source encodes clock in signal – 5– Synchronous: - source & dest on same clock Long: - stream of logical values at a time Wide: - control, data and timing on separate wires CS 495 S’ 02

Buses P P P Bus • Simple and cost-effective for small-scale multiprocessors • Not scalable (limited bandwidth; electrical complications) – 6– CS 495 S’ 02

Crossbars • Each port has link to every other port + Low latency and high throughput - Cost grows as O(N^2) so not very scalable. - Difficult to arbitrate and to get all data lines into and out of a centralized crossbar. • Used in small-scale MPs (e. g. , C. mmp) and as building block for other networks (e. g. , Omega). – 7– CS 495 S’ 02

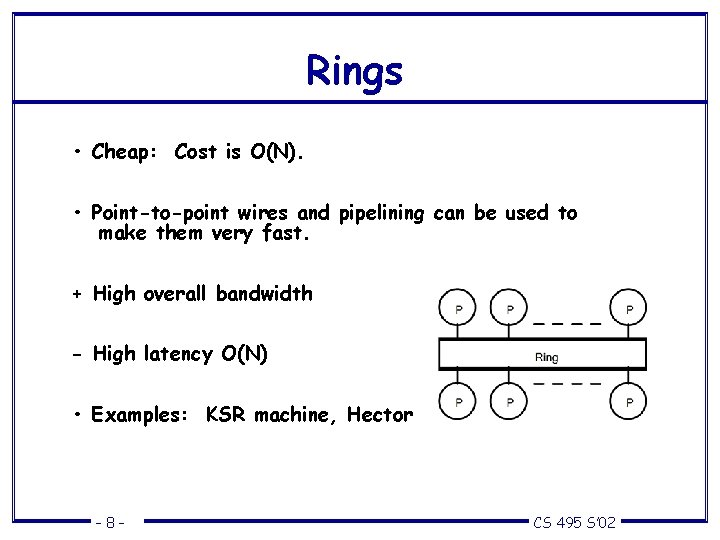
Rings • Cheap: Cost is O(N). • Point-to-point wires and pipelining can be used to make them very fast. + High overall bandwidth - High latency O(N) • Examples: KSR machine, Hector – 8– CS 495 S’ 02

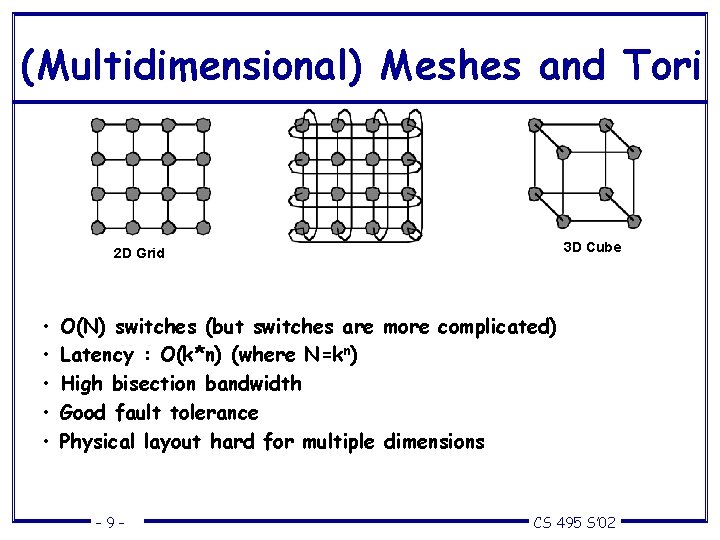
(Multidimensional) Meshes and Tori 3 D Cube 2 D Grid • • • O(N) switches (but switches are more complicated) Latency : O(k*n) (where N=kn) High bisection bandwidth Good fault tolerance Physical layout hard for multiple dimensions – 9– CS 495 S’ 02

Real World 2 D mesh 1824 node Paragon: 16 x 114 array – 10 – CS 495 S’ 02

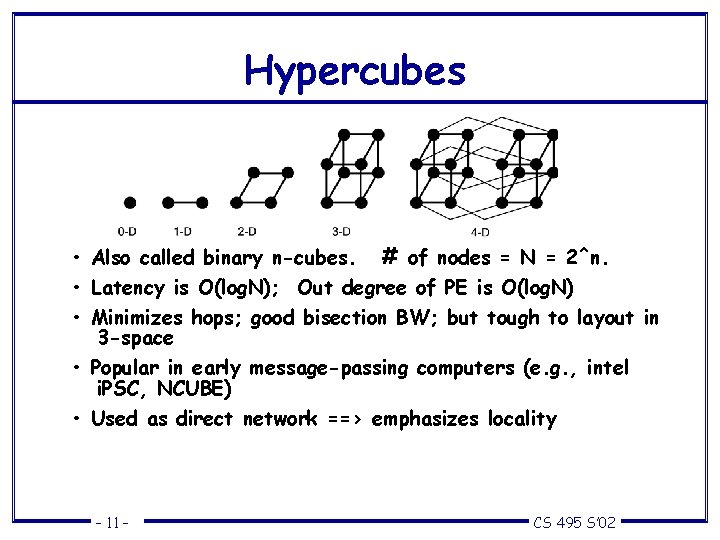
Hypercubes • Also called binary n-cubes. # of nodes = N = 2^n. • Latency is O(log. N); Out degree of PE is O(log. N) • Minimizes hops; good bisection BW; but tough to layout in 3 -space • Popular in early message-passing computers (e. g. , intel i. PSC, NCUBE) • Used as direct network ==> emphasizes locality – 11 – CS 495 S’ 02

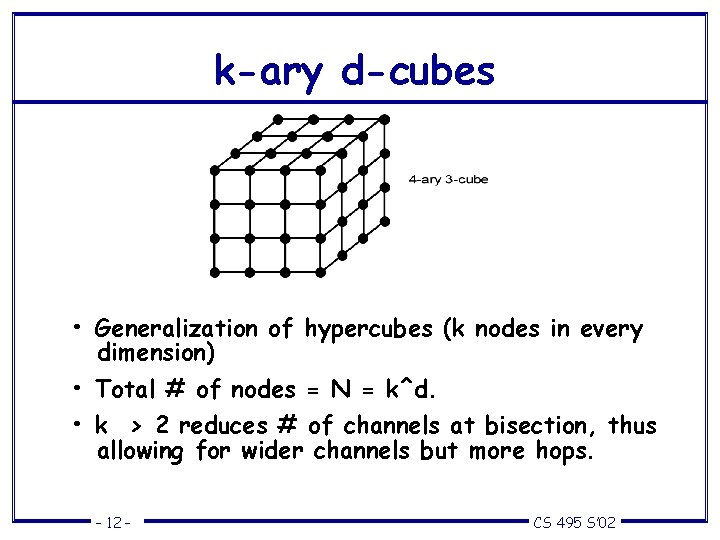
k-ary d-cubes • Generalization of hypercubes (k nodes in every dimension) • Total # of nodes = N = k^d. • k > 2 reduces # of channels at bisection, thus allowing for wider channels but more hops. – 12 – CS 495 S’ 02

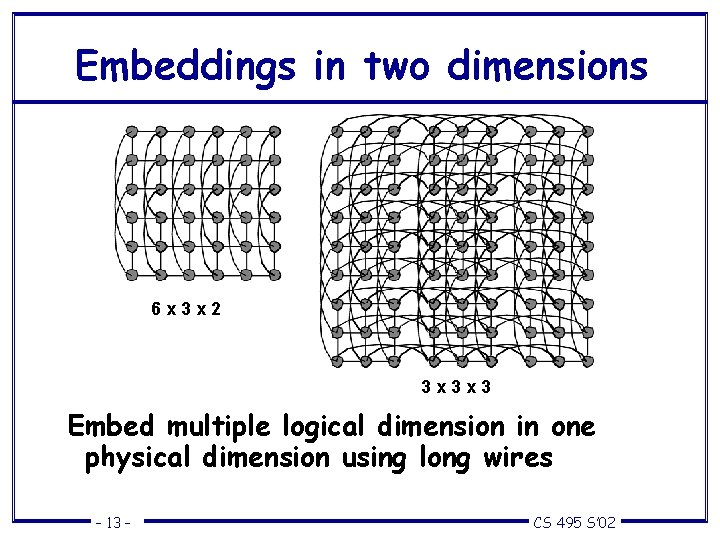
Embeddings in two dimensions 6 x 3 x 2 3 x 3 x 3 Embed multiple logical dimension in one physical dimension using long wires – 13 – CS 495 S’ 02

Trees • Cheap: Cost is O(N). • Latency is O(log. N). • Easy to layout as planar graphs (e. g. , H-Trees). • For random permutations, root can become bottleneck. • To avoid root being bottleneck, notion of Fat-Trees (used in CM 5) – 14 – CS 495 S’ 02

Multistage Logarithmic Networks Key Idea: have multiple layers of switches between destinations. • Cost is O(Nlog. N); latency is O(log. N); throughput is O(N). • Generally indirect networks. • Many variations exist (Omega, Butterfly, Benes, . . . ). • Used in many machines: BBN Butterfly, IBM RP 3, . . . – 15 – CS 495 S’ 02

Omega Network • All stages are same, so can use recirculating network. • Single path from source to destination. • Can add extra stages and pathways to minimize collisions and increase fault tolerance. • Can support combining. Used in IBM RP 3. – 16 – CS 495 S’ 02

Butterfly Network • Equivalent to Omega network. Easy to see routing of messages. • Also very similar to hypercubes (direct vs. indirect though). • Clearly see that bisection of network is (N / 2) channels. • Can use higher-degree switches to reduce depth. – 17 – CS 495 S’ 02

Properties of Some Topologies Topology Degree Diameter Ave Dist Bisection D (D ave) @ P=1024 1 D Array 2 N-1 N/3 1 huge 1 D Ring 2 N/4 2 huge 2 D Mesh 4 2 (N 1/2 - 1) 2/3 N 1/2 63 (21) 2 D Torus 4 N 1/2 2 N 1/2 32 (16) dk/2 dk/4 15 (7. 5) @d=3 n/2 N/2 10 (5) k-ary d-cube 2 d Hypercube – 18 – n=log. N n CS 495 S’ 02

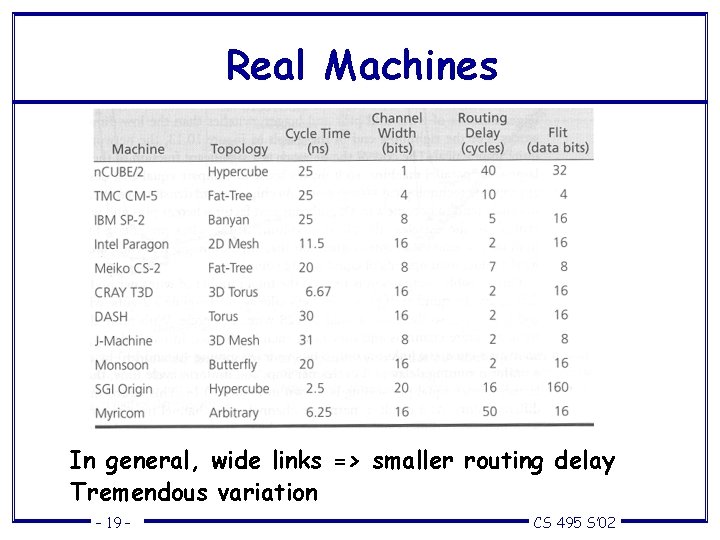
Real Machines In general, wide links => smaller routing delay Tremendous variation – 19 – CS 495 S’ 02

How many dimensions? d = 2 or d = 3 • Short wires, easy to build • Many hops, low bisection bandwidth • Requires traffic locality d >= 4 • Harder to build, more wires, longer average length • Fewer hops, better bisection bandwidth • Can handle non-local traffic k-ary d-cubes provide a consistent framework for comparison • N = kd • scale dimension (d) or nodes per dimension (k) • assume cut-through – 20 – CS 495 S’ 02

Scaling k-ary d-cubes What is equal cost? • Equal number of nodes? • Equal number of pins/wires? • Equal bisection bandwidth? • Equal area? • Equal wire length? Each assumption leads to a different optimum Recall: switch degree: d diameter = d(k-1) total links = N*d pins per node = 2 wd bisection = kd-1 = N/d links in each directions 2 Nw/d wires cross the middle – 21 – CS 495 S’ 02

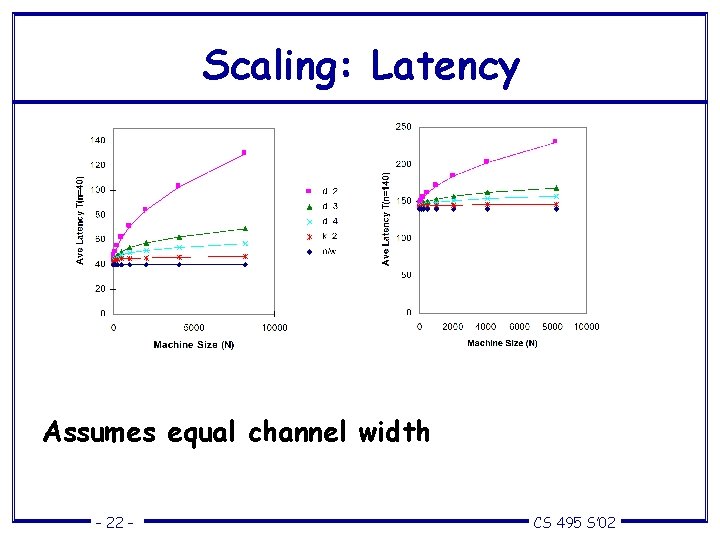
Scaling: Latency Assumes equal channel width – 22 – CS 495 S’ 02

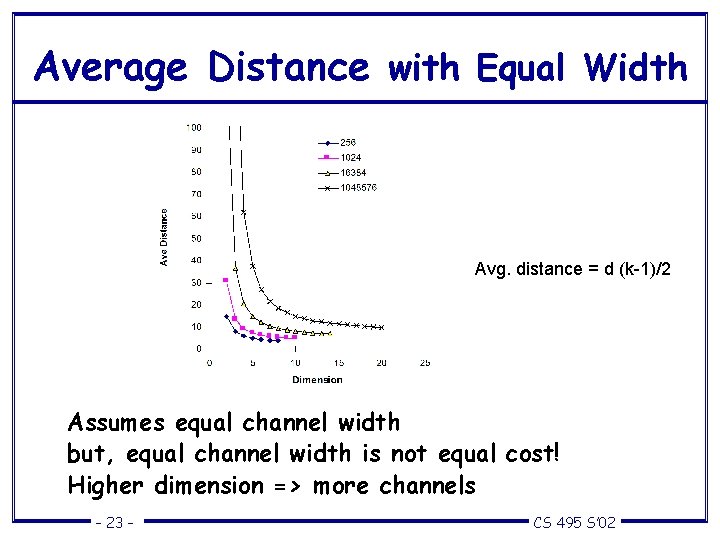
Average Distance with Equal Width Avg. distance = d (k-1)/2 Assumes equal channel width but, equal channel width is not equal cost! Higher dimension => more channels – 23 – CS 495 S’ 02

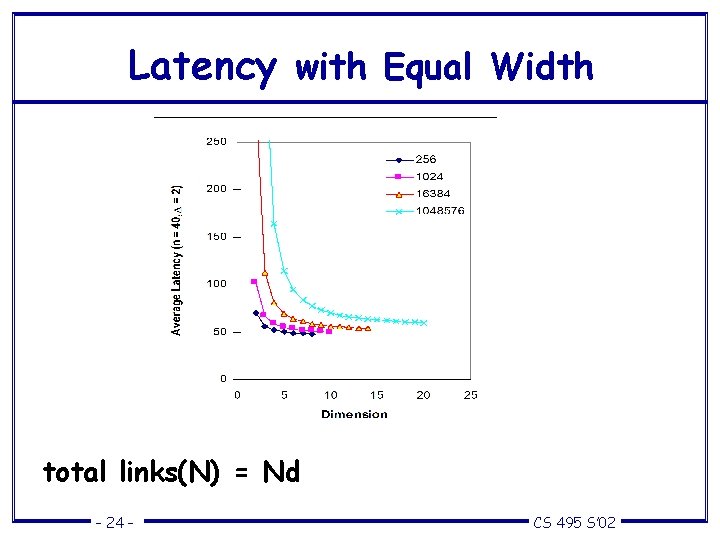
Latency with Equal Width total links(N) = Nd – 24 – CS 495 S’ 02

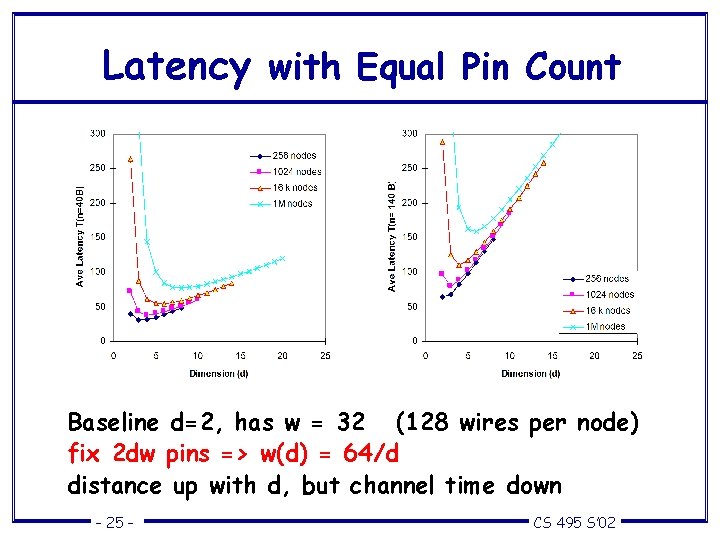
Latency with Equal Pin Count Baseline d=2, has w = 32 (128 wires per node) fix 2 dw pins => w(d) = 64/d distance up with d, but channel time down – 25 – CS 495 S’ 02

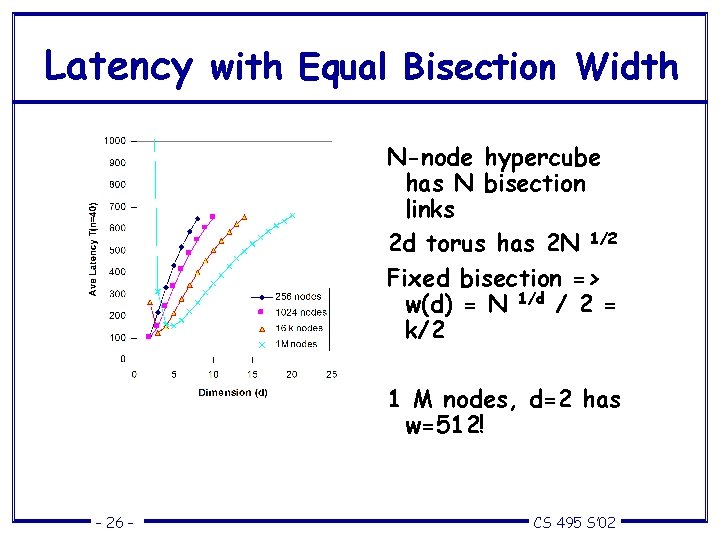
Latency with Equal Bisection Width N-node hypercube has N bisection links 2 d torus has 2 N 1/2 Fixed bisection => w(d) = N 1/d / 2 = k/2 1 M nodes, d=2 has w=512! – 26 – CS 495 S’ 02

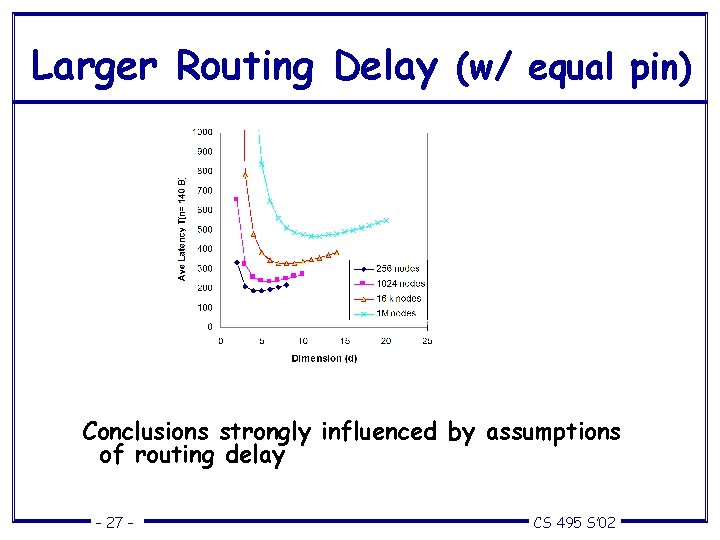
Larger Routing Delay (w/ equal pin) Conclusions strongly influenced by assumptions of routing delay – 27 – CS 495 S’ 02

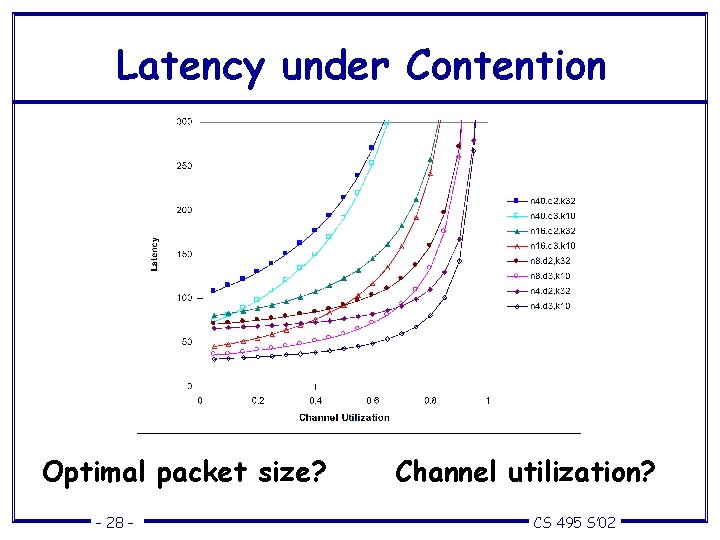
Latency under Contention Optimal packet size? – 28 – Channel utilization? CS 495 S’ 02

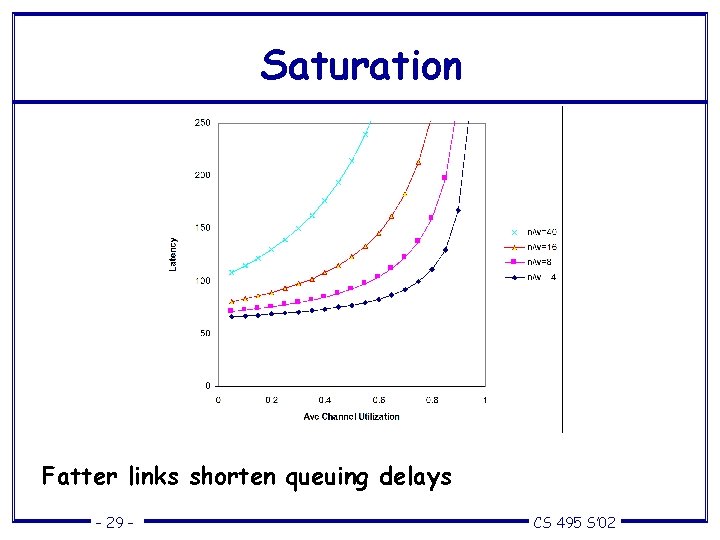
Saturation Fatter links shorten queuing delays – 29 – CS 495 S’ 02

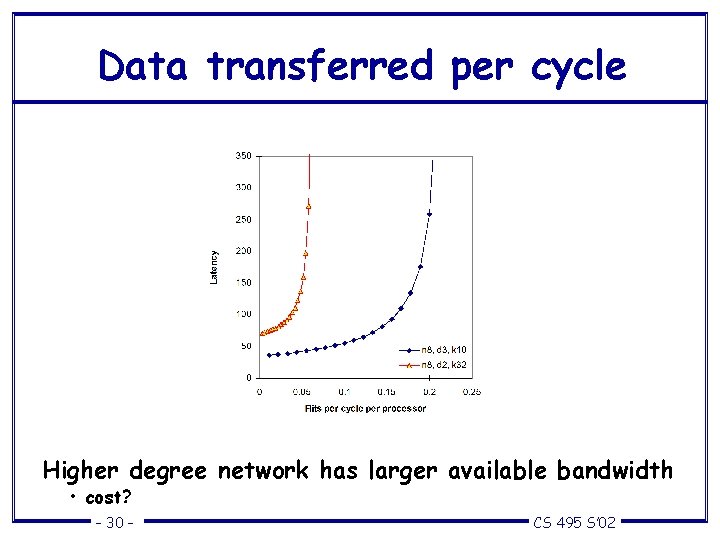
Data transferred per cycle Higher degree network has larger available bandwidth • cost? – 30 – CS 495 S’ 02

Advantages of Low-Dimensional Nets What can be built in VLSI is often wire-limited LDNs are easier to layout: • more uniform wiring density (easier to embed in 2 -D or 3 -D space) • mostly local connections (e. g. , grids) Compared with HDNs (e. g. , hypercubes), LDNs have: • shorter wires (reduces hop latency) • fewer wires (increases bandwidth given constant bisection width) – increased channel width is the major reason why LDNs win! LDNs have better hot-spot throughput • more pins per node than HDNs – 31 – CS 495 S’ 02

Routing Recall: routing algorithm determines • which of the possible paths are used as routes • how the route is determined • R: N x N -> C, which at each switch maps the destination node nd to the next channel on the route Issues: • Routing mechanism – arithmetic – source-based port select – table driven – general computation • Properties of the routes • Deadlock free – 32 – CS 495 S’ 02

Store&Forward vs Cut-Through Routing h(n/b + D) vs n/b + h D h: hops, n: packet length, b: badwidth, D: routing delay at each switch – 33 – CS 495 S’ 02

Routing Mechanism need to select output port for each input packet • in a few cycles Reduce relative address of each dimension in order • Dimension-order routing in k-ary d-cubes • e-cube routing in n-cube – 34 – CS 495 S’ 02

Routing Mechanism (cont) P 3 P 2 P 1 P 0 Source-based • • message header carries series of port selects used and stripped en route CRC? Packet Format? CS-2, Myrinet, MIT Artic Table-driven • message header carried index for next port at next switch – o = R[i] • table also gives index for following hop – o, I’ = R[i ] • ATM, HPPI – 35 – CS 495 S’ 02

Properties of Routing Algorithms Deterministic • route determined by (source, dest), not intermediate state (i. e. traffic) Adaptive • route influenced by traffic along the way Minimal • only selects shortest paths Deadlock free • no traffic pattern can lead to a situation where no packets mover forward – 36 – CS 495 S’ 02

Deadlock Freedom How can it arise? • necessary conditions: – shared resource – incrementally allocated – non-preemptible • think of a channel as a shared resource that is acquired incrementally – source buffer then dest. buffer – channels along a route How do you avoid it? • constrain how channel resources are allocated • ex: dimension order How do you prove that a routing algorithm is deadlock free – 37 – CS 495 S’ 02

Proof Technique Resources are logically associated with channels Messages introduce dependences between resources as they move forward Need to articulate possible dependences between channels Show that there are no cycles in Channel Dependence Graph • find a numbering of channel resources such that every legal route follows a monotonic sequence => no traffic pattern can lead to deadlock Network need not be acyclic, only channel dependence graph – 38 – CS 495 S’ 02

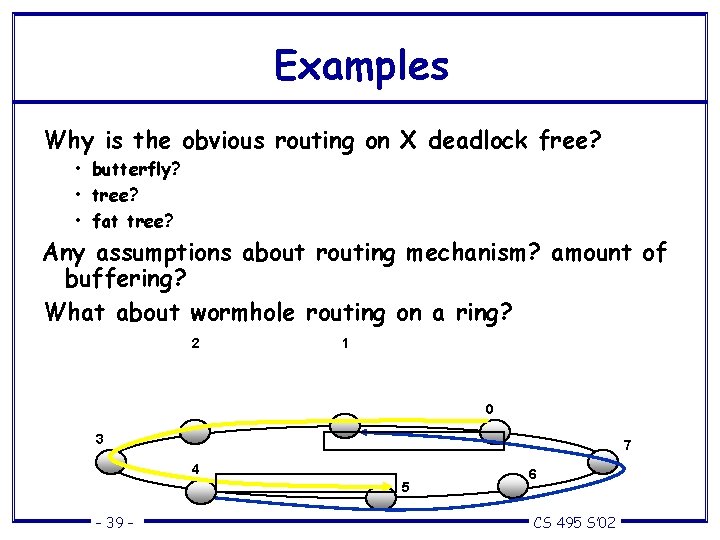
Examples Why is the obvious routing on X deadlock free? • butterfly? • tree? • fat tree? Any assumptions about routing mechanism? amount of buffering? What about wormhole routing on a ring? 2 1 0 3 7 4 5 – 39 – 6 CS 495 S’ 02

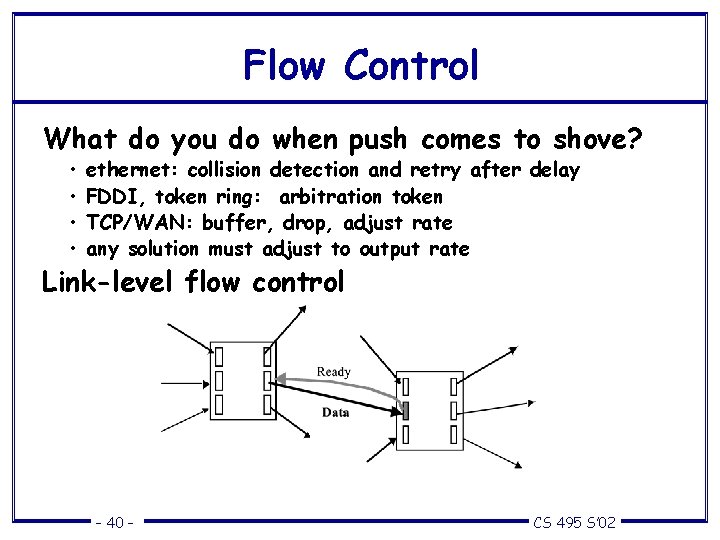
Flow Control What do you do when push comes to shove? • • ethernet: collision detection and retry after delay FDDI, token ring: arbitration token TCP/WAN: buffer, drop, adjust rate any solution must adjust to output rate Link-level flow control – 40 – CS 495 S’ 02

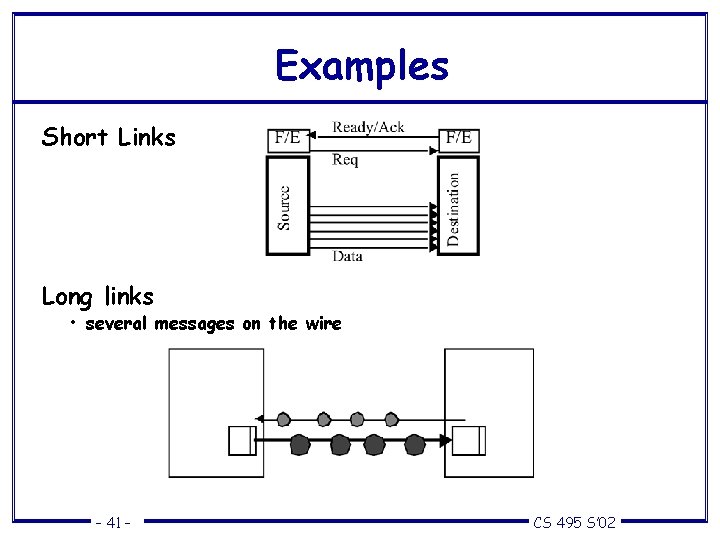
Examples Short Links Long links • several messages on the wire – 41 – CS 495 S’ 02

Link vs global flow control Hot Spots Global communication operations Natural parallel program dependences – 42 – CS 495 S’ 02

Case study: Cray T 3 E • 3 -dimensional torus, with 1024 switches each connected to 2 processors • Short, wide, synchronous links • Dimension order, cut-through, packetswitched routing • Variable sized packets, in multiples of 16 bits – 43 – CS 495 S’ 02

Case Study: SGI Origin • Hypercube-like topologies with upto 256 switches • Each switch supports 4 processors and connects to 4 other switches • Long, wide links • Table-driven routing: programmable, allowing for flexible topologies and fault-avoidance – 44 – CS 495 S’ 02