Clustering Social Networks Nina Mishra et al Presented

Clustering Social Networks Nina Mishra et al Presented by Nam Nguyen

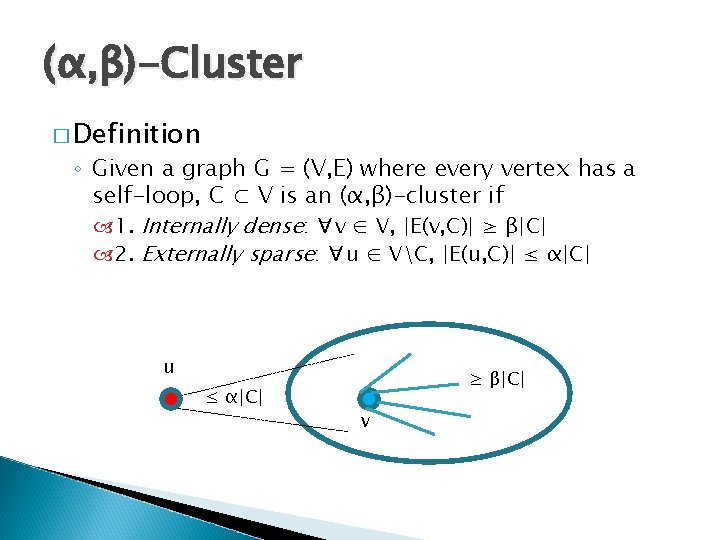
(α, β)-Cluster � Definition ◦ Given a graph G = (V, E) where every vertex has a self-loop, C ⊂ V is an (α, β)-cluster if 1. Internally dense: ∀v ∈ V, |E(v, C)| ≥ β|C| 2. Externally sparse: ∀u ∈ VC, |E(u, C)| ≤ α|C| u ≤ α|C| ≥ β|C| v

Example � {a, b, c, d} and {d, e, f, g} are (1/4, 1)-clusters � h and i are do not fall into any (α, β)-cluster for 0≤ α< ½ < β ≤ 1 thus, they would not be clustered. (α, β)-cluster are able for detecting overlapping clusters.

Problem definition Objective Identify clusters that are internally dense, i. e. , each vertex in the cluster is adjacent to at least a β-fraction of the cluster, and externally sparse, i. e. , any vertex outside of the cluster is adjacent to at most an α– fraction of the vertices in the cluster. Given 0≤ α< β ≤ 1, find all (α, β)-clusters in the network

Contributions of the paper � Give a bound for the overlapping of two (α, β)clusters A and B. ◦ They overlap in at most |C|*min{1 -(β- α), α/(2β-1)} vertices. � If the ratio of |A| and |B| is at most (1 - α)/(1 - β) then one cluster can not be contained in the other. � Give a loose upper bound for the number of (α, 1)clusters of size s: O( (n/s) α+1 ) � Introduction of the ρ-champion of a cluster and if β> ½(1+ ρ+ α), there is a simple deterministic algorithm for finding all such clusters in time O(m 0. 7 n 1. 2 + n 2+o(1))

Some minor remarks �β 1, the cluster C a clique � α 0, C tends to a disconnected component � β< ½ then C might contain two disconnected components. � We want α < β and β> ½. � (0, β)-clusters finding connected components & output β-connected ones. � (1 -1/n, 1)-clusters finding the maximal cliques in a graph. � ((1 -ε) β, β)-clusters finding quasi-cliques.

Result 1 � Question: ◦ How about the intersection of 3 (or more) (α, β)-clusters of the same size? different size ? ◦ How about the intersection of an (α, β)-cluster and an (α’, β’)-cluster of the same size? different size ?

Result 2: Bounding the number of (α, 1)-clusters � Proof ◦ Two clusters of the same size s can share at most αs vertices. ◦ Every subset of size (αs+1) must appear in at most one set in C. ◦ There are subsets of s elements from n elements, each of these contains subsets of size (αs+1). ◦ Therefore, we can have at most clusters in C ◦ |C| ≤ =

This bound is tight … � when α=0 ◦ No overlapping # of clusters of size s = n/s. � when α 1 ( α = (n-1)/n ) ◦ Consider the complement of the following graph ◦ Let s = n = N/2, then the bound is 2 n. ◦ In fact, we do have 2 n subsets of (α, 1)-clusters of size n by choosing from the set B = {b 1 b 2…bn | bi is either xi or yi}

An algorithm for finding clusters with champions � Why? ◦ In last example, each vertex has as many neighbors outside as within the cluster ◦ There is no vertex that “champions” the cluster (having more friends inside than outside) ◦ Why not find one who champions and start with it?

Algorithm (cont’d) � Assumption: ◦ A big gap between β and α/2: β > ½ + (α+ρ)/2 � Why? ◦ Recall last example: We have 2 n possible clusters of size n Too many ◦ Any algorithm that outputs more clusters than nodes are undesirable. ◦ Thus, we need some restriction to reduce the # of returned clusters.

Algorithm (cont’d) � How many clusters with ρ-champion should we have ? � How to find them? ◦ A big gap between β and α/2: β > ½ + (α+ρ)/2

Algorithm (cont’d) If v and c have sufficient many neighbors then v is a part of the cluster C that c champions. that’s what line #5 for Running time of the algorithm

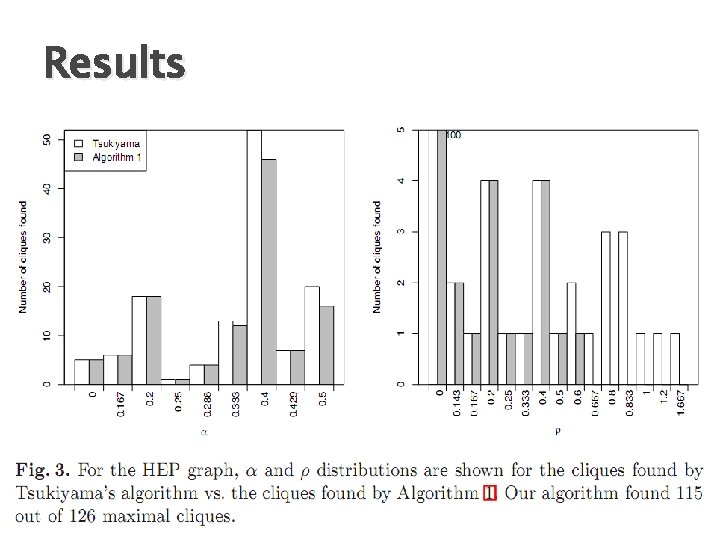
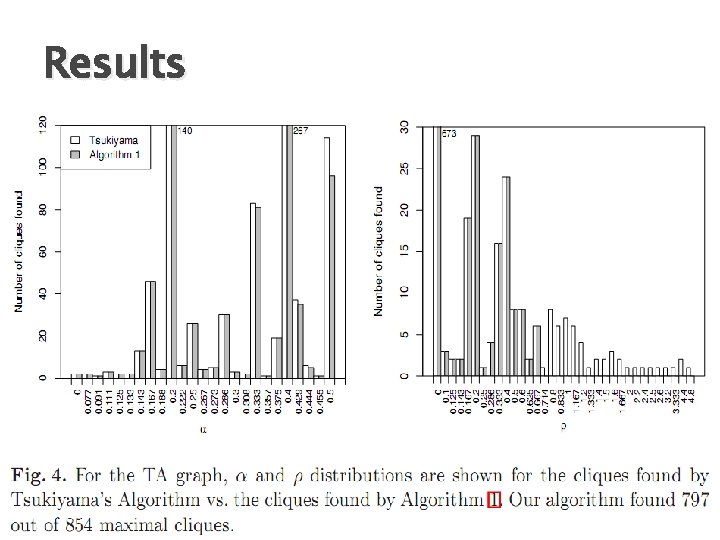
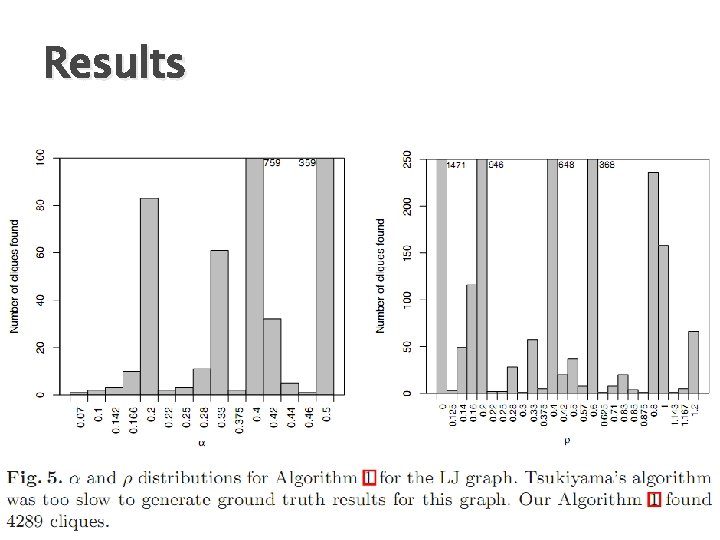
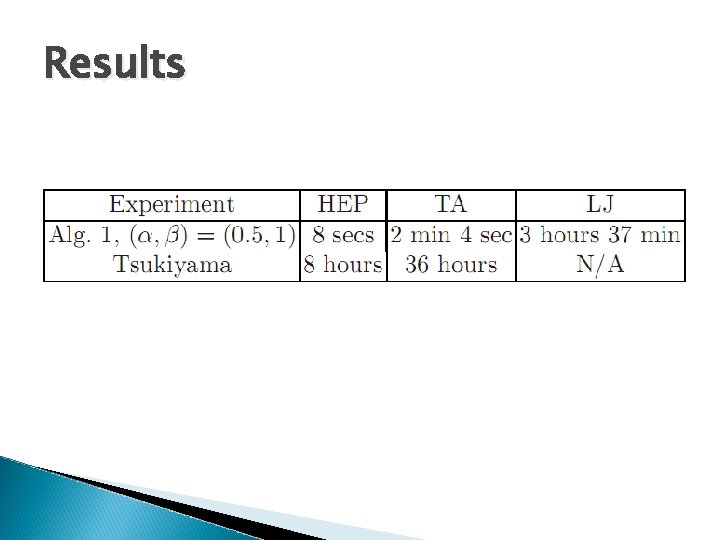
Experimental Results � For real networks ◦ Do (α, β)-clusters with ρ-champion exist? use Tsukiayama algorithm ◦ If they do exist, do most (α, β)-clusters have ρ-champion? � Results ◦ Able to find ~90% of the maximal cliques in graphs where α ≤ ½. ◦ No strong ρ-champions in missed clusters. ◦ Running time: Weight faster than Tsukiyama’s algorithm � Datasets ◦ High Energy Physics Theory Co-Author graph (HEP) ◦ Theory Co-Author graph (TA) ◦ A subset of Live Journal graph (LP)

Results

Results

Results

Results

References � [1] Clustering Social Networks, Ninna Mishra, Robert Schreiber, Isabelle Stanton and Robert E. Tarjan (2007)