Movimiento de rodamiento momento angular y momento de






- Slides: 12

Movimiento de rodamiento, momento angular y momento de torsión Física I

Contenido • • • Rodamiento de un cuerpo rígido Producto vectorial Cálculo del producto cruz Momento angular de una partícula Momento angular de un sistema de partículas Rotación de un cuerpo rígido alrededor de un eje fijo • Conservación del momento angular

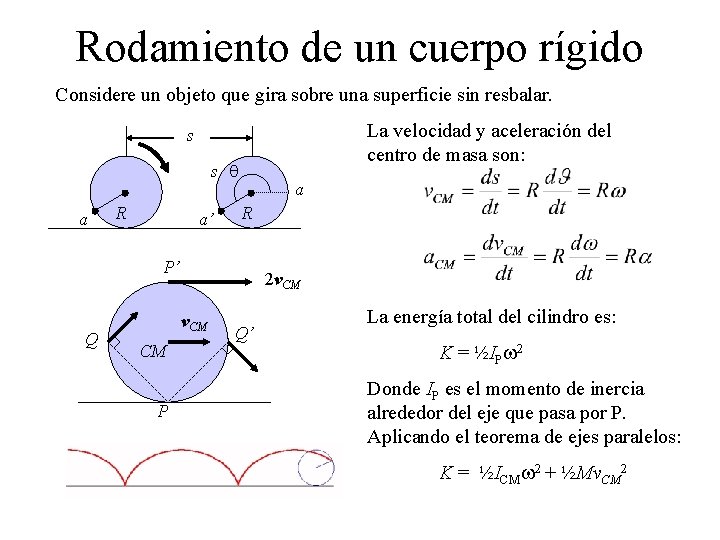
Rodamiento de un cuerpo rígido Considere un objeto que gira sobre una superficie sin resbalar. La velocidad y aceleración del centro de masa son: s s q a R a’ a R P’ Q 2 v. CM CM P Q’ La energía total del cilindro es: K = ½IPw 2 Donde IP es el momento de inercia alrededor del eje que pasa por P. Aplicando el teorema de ejes paralelos: K = ½ICMw 2 + ½Mv. CM 2

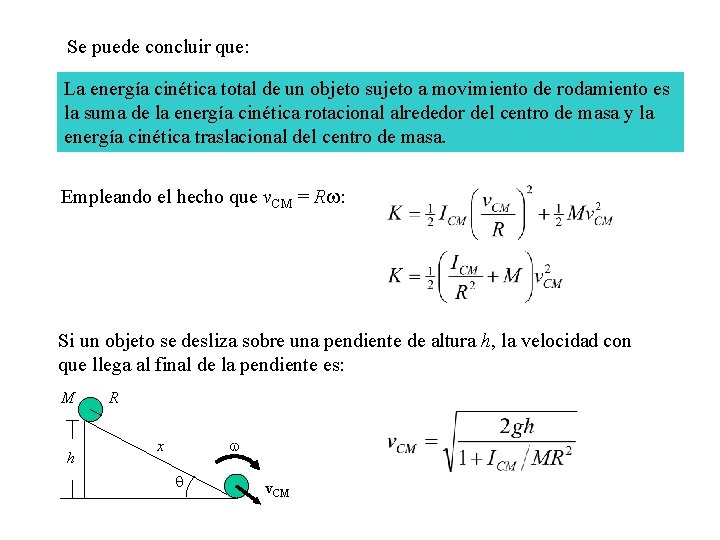
Se puede concluir que: La energía cinética total de un objeto sujeto a movimiento de rodamiento es la suma de la energía cinética rotacional alrededor del centro de masa y la energía cinética traslacional del centro de masa. Empleando el hecho que v. CM = Rw: Si un objeto se desliza sobre una pendiente de altura h, la velocidad con que llega al final de la pendiente es: M h R w x q v. CM

Ejemplo Calcular velocidades de cuerpos que bajan por pendiente Aro o cascarón cilíndrico Cilindro sólido o disco Esfera sólida Esfera hueca Barra delgada larga con eje de rotación que pasa por el centro.

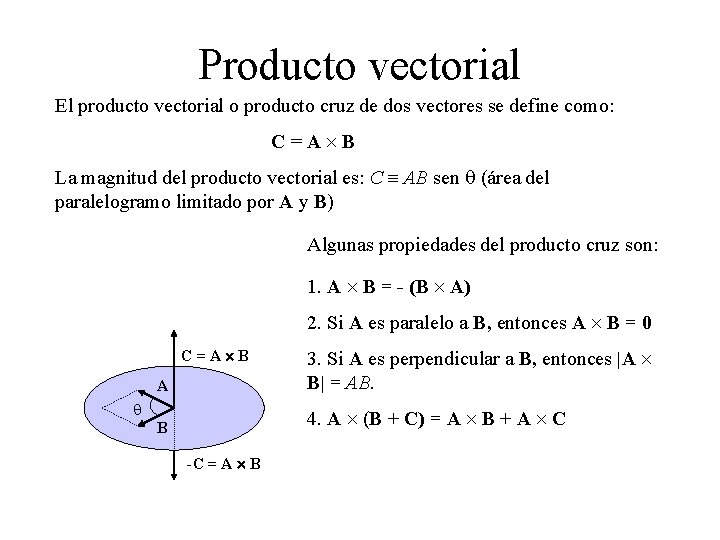
Producto vectorial El producto vectorial o producto cruz de dos vectores se define como: C=A B La magnitud del producto vectorial es: C AB sen q (área del paralelogramo limitado por A y B) Algunas propiedades del producto cruz son: 1. A B = - (B A) 2. Si A es paralelo a B, entonces A B = 0 A 3. Si A es perpendicular a B, entonces |A B| = AB. B 4. A (B + C) = A B + A C C=A B q -C = A B

Cálculo del producto cruz De las propiedades del producto cruz se desprenden los siguientes resultados: i i = j j = k k =0 i j = –j i = k j k = –k j = i k i = –i k = j De esto se desprende que el producto cruz de dos vectores se puede evaluar con el determinante:

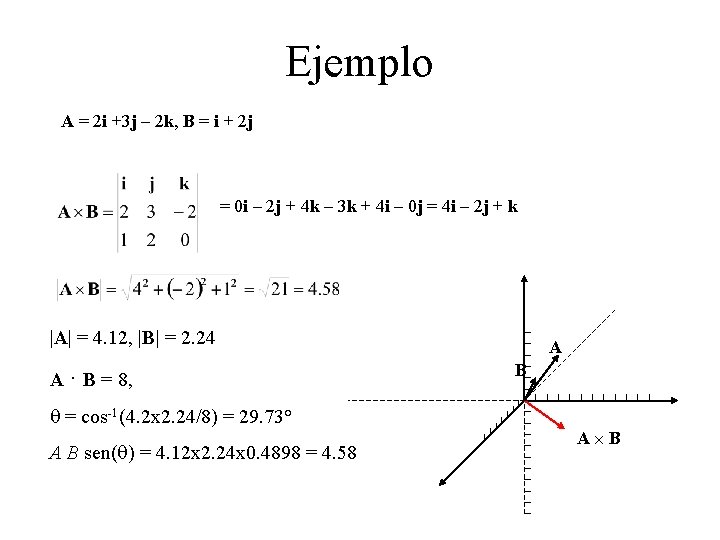
Ejemplo A = 2 i +3 j – 2 k, B = i + 2 j = 0 i – 2 j + 4 k – 3 k + 4 i – 0 j = 4 i – 2 j + k |A| = 4. 12, |B| = 2. 24 A · B = 8, q = cos-1(4. 2 x 2. 24/8) = 29. 73° A B sen(q) = 4. 12 x 2. 24 x 0. 4898 = 4. 58 A B

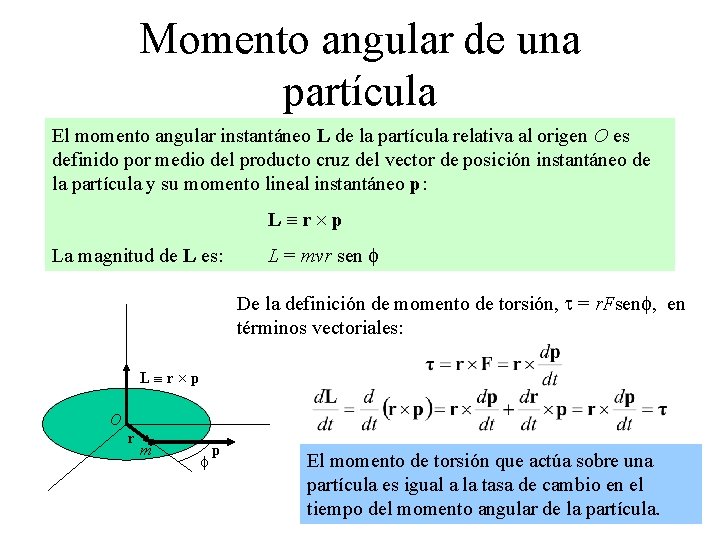
Momento angular de una partícula El momento angular instantáneo L de la partícula relativa al origen O es definido por medio del producto cruz del vector de posición instantáneo de la partícula y su momento lineal instantáneo p: L r p La magnitud de L es: L = mvr sen f De la definición de momento de torsión, t = r. Fsenf, en términos vectoriales: L r p O r m f p El momento de torsión que actúa sobre una partícula es igual a la tasa de cambio en el tiempo del momento angular de la partícula.

Momento angular de un sistema de partículas El momento angular de un sistema de partículas es la suma vectorial de los momentos angulares de cada partícula: L = L 1 + L 2 +. . . + Ln = Li Por lo tanto concluimos que: La tasa de cambio en el tiempo del momento angular total del sistema alrededor de algún origen en un marco inercial es igual al momento de torsión externo neto que actúa sobre el sistema en torno a ese origen.

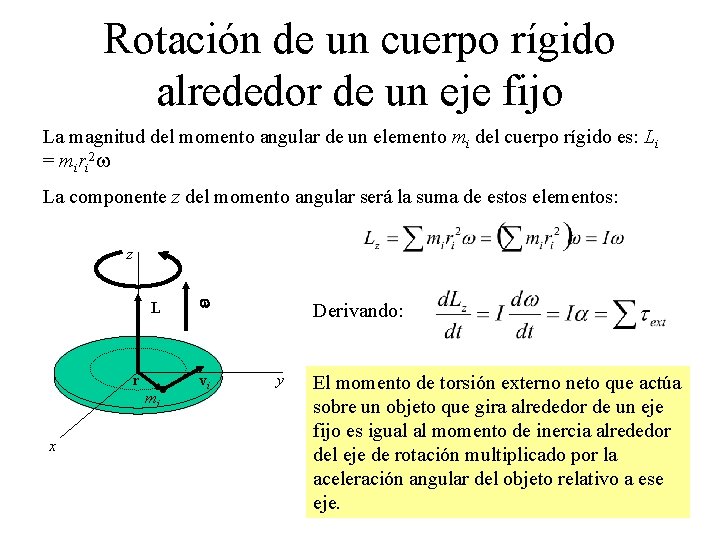
Rotación de un cuerpo rígido alrededor de un eje fijo La magnitud del momento angular de un elemento mi del cuerpo rígido es: Li = miri 2 w La componente z del momento angular será la suma de estos elementos: z L r mi x w vi Derivando: y El momento de torsión externo neto que actúa sobre un objeto que gira alrededor de un eje fijo es igual al momento de inercia alrededor del eje de rotación multiplicado por la aceleración angular del objeto relativo a ese eje.

Conservación del momento angular El momento angular total de un sistema es constante si el momento de torsión externo resultante que actúa sobre el sistema es cero. Si Entonces L = constante o Iiwi = Ifwf El momento de torsión resultante que actúa sobre un cuerpo alrededor de un eje que pasa por el centro de masa es igual a la tasa de cambio en el tiempo del momento angular independientemente del movimiento del centro de masa.